Оценить адекватность регрессионной модели:
1. Вычислить n значений температуры воды по уравнению регрессии y* (x) = ax + b.
2. Построить график вычисленных y* и фактических y значений температуры воды (рисунок 3).
3. Рассчитать дисперсию модели y *, характеризующую изменчивость линии регрессии относительно среднего значения 
,
,
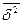– объясненная уравнением регрессии дисперсия.
4. Рассчитать остаточную дисперсию 
, характеризующую отклонение уравнения регрессии от результатов наблюдений у,
.
5. Вычислить коэффициент детерминации по формуле
.
Коэффициент детерминации показывает долю дисперсии исходного ряда, которая описывается моделью регрессии.
Применяя неравенство
,
сделать вывод об отклонении от линейности.
Рисунок 3 – Фактические и вычисленные по уравнению регрессии значения
температуры воды в декабре в точке 9 (55° с.ш. 30° з.д.)
6. Оценить адекватность регрессионной модели. Для этого выдвинуть нулевую гипотезу о равенстве дисперсий
H0: 
.
Для ее проверки использовать F - критерий Фишера. Вычислить дисперсионное отношение
Fкрит = 
,
которое сравнивается с Fтабл (v 1, v 2,a) при заданном уровне значимости a, a = 0.05, и степенях свободы v 1 = 1, v 2 = n – 2 (см. Таблицу 4 Приложения 2).
Если Fкрит > Fтабл, то нулевая гипотеза о равенстве дисперсий отвергается, что означает в рассматриваемом случае адекватность регрессионной модели.
7. Проанализировать качество полученной регрессионной модели, учитывая, что для хорошей модели необходимо выполнение следующих условий:
1) коэффициент корреляции должен быть значим;
2) все коэффициенты регрессии должны быть значимы;
3) модель должна быть адекватна;
4) коэффициент детерминации должен быть больше 0.7;
5) стандартная ошибка модели se должна быть меньше 0.67 стандартного отклонения Sy исходного ряда Y.
Пример расчетов представлен в таблице 2.
Индивидуальная РАБОТА № 2
Задание 1
Построение автокорреляционной функции
Построить и проанализировать автокорреляционную функцию третьего временного ряда температуры воды (обозначим через yt, 
). Для этого:
1. Вычислить автокорреляционную функцию rs для каждого из сдвигов s по формуле
,
где T – длина реализации, s – сдвиг, который меняется от 1 до максимума, например, smax = 13.
В силу четности автокорреляционной функции временной ряд можно сдвигать в любую сторону (вперед или назад).
2. Построить график автокорреляционной функции.
3. Проанализировать полученные результаты. Указать на тип случайного процесса, характеризующий графики автокорреляционных функций («белый шум», «цветной шум», цикличность т.д.).
Задание 2
