Рассчитать основные параметры трех статистических рядов:
1. Выборочное среднее (среднее арифметическое), характеризующее центр тяжести числового ряда
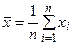
 ,
,
где n – длина ряда, k – число групп, mi – абсолютные частоты,  – i -ая варианта дискретного вариационного ряда.
– i -ая варианта дискретного вариационного ряда.
Указание: правильность вычисления выборочного среднего проверить с помощью встроенной статистических функций СРЗНАЧ приложения MS Eхcel.
2. Выборочную дисперсию
Sn 2 =  .
.
3. Исправленную выборочную дисперсию
sn 2 =  .
.
4. Стандартное отклонение (выборочное среднее квадратическое отклонение)  .
.
Указание: правильность вычисления выборочной дисперсии, исправленной выборочной дисперсии и стандартного отклонения проверить с помощью встроенных статистических функций ДИСПР, ДИСП и СТАНДОТКЛОНП приложения MS Eхcel.
5. Коэффициент вариации
V S = Sn /  .
.
Параметры Sn 2, Sn и V S характеризуют рассеивание ряда относительно центра тяжести числового ряда и отличаются друг от друга размерностью.
6. Коэффициент асимметрии, показывающий степень асимметричности ряда относительно его центра,
 .
.
7. Коэффициент эксцесса, характеризующий крутость (островершинность и плосковершинность) эмпирической кривой распределения,
 .
.
8. Медиану – центральное значение ранжированного ряда x* (1) £ x* (2)£ … £ x* (п),
Ме = 
Указание: правильность вычисления медианы проверить с помощью встроенной статистической функции МЕДИАНА приложения MS Eхcel.
9. Моду (или моды), представляющую наиболее вероятное (часто встречающееся) значение исходного ряда. Мода может быть одна, две или несколько. Соответственно, распределение называют одномодальным, бимодальным или полимодальным.
Пример расчетов приводится в таблице 1.
Таблица 1.
Основные статистические параметры температуры поверхности океана
в октябре, ноябре, декабре (1957-1993 гг.) в точке 9 (55о с.ш. 30о з.д.)
| октябрь | ноябрь | декабрь | Вывод | |
| Среднее арифметическое | 10,56 | 9,27 | 8,60 | |
| Выборочная дисперсия | 0,27 | 0,28 | 0,38 | |
| Выборочная исправленная дисперсия | 0,28 | 0,29 | 0,39 | |
| Стандартное отклонение | 0,52 | 0,53 | 0,61 | |
| Коэффициент вариации | 0,05 | 0,06 | 0,07 | Для трех рядов характерна высокая степень концентрации относительно среднего |
| Коэффициент асимметрии | 0,31 | -0,30 | -0,48 | Для трех рядов характерна умеренная асимметрия; для первого ряда распределение скошено вправо; для второго и третьего – распределение скошено влево. |
| Коэффициент эксцесса | 0,09 | 0,70 | -0,24 | Эмпирические кривые распределений приближены к нормальному; для первого и второго ряда распределение имеет острый пик; для третьего – распределение имеет плосковершинную форму. |
| Мода (моды) | 10,4 | 9,10 | 8,90 | |
| медиана | 10,50 | 9,30 | 8,60 |
Провести анализ полученных результатов: сравнить основные статистические параметры для трех месяцев, указать физический смысл полученных значений коэффициента вариации, асимметрии, эксцесса, моды.
10. С использованием средств анализа данных пакета MS Excel (см. Приложение 4), найти основные характеристики трех исследуемых несгруппированных температурных рядов.
Задание 3






