1. Построить корреляционное поле для второго (обозначим через X) и третьего (обозначим через Y) рядов температуры воды (рисунок 2). Сделать предварительный вывод.
2. Оценить взаимосвязь рядов X и Y температуры воды путем расчета коэффициента корреляции между ними
,
где S х =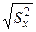 
, Sу = 
, 
, 
, 
. Сделать вывод.
Указание: правильность вычисления ковариации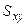 
и коэффициента корреляции 
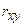проверить с помощью встроенных статистических функций КОВАР и ПИРСОН приложения MS Eхcel.
3. Определить значимость коэффициента корреляции rxy. Для этого:
а) вычислить среднеквадратическую ошибку sr линейного коэффициента корреляции:
;
б) выдвинуть нулевую гипотезу H0: rxy = 0, для проверки которой рассчитать критерий Стьюдента t расч:
t расч =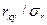 
.
По статистической Таблице 2 Приложения 2 критических точек t - распределения Стьюдента, по заданному уровню значимости aи числу степеней свободы k = n – 2 найти критическую точку tкр (k, a) двусторонней критической области.
Если | t расч | < tкр (k, a) – нет оснований отвергнуть нулевую гипотезу.
Если | t расч| > tкр (k, a) – нулевую гипотезу отвергают, отклонение от rxy нуля носит неслучайный характер, и, следовательно, величина rxy значима.
Указание: значение критической точки tкр (k, a) можно получить, применяя встроенную статистическую функцию СТЬЮДРАСПОБР приложения MS Excel.
4. Для коэффициента корреляции rxy и случая двухмерного нормального распределения построить доверительный интервал (q, 
) с надежностью g = 1 – a:
q = 
,
где п – объем выборки,
, 
,
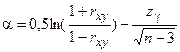значения функции Лапласа
Ф0(zg) = g/2, Ф0(z)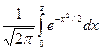 
приведены в Таблице 1 Приложения 2.
Указание: значения уровней значимости a выбрать самостоятельно: 0.01; 0.02; 0.10 и т.д.
Пример расчета представлен в таблице 2.
Таблица 2.
Модель линейной регрессии связи температуры воды в декабре и ноябре (1957-1983 гг.)
в точке 9 (55о с.ш. 30о з.д.), ее параметры и оценка их значимости
| Выборочные характеристики | |||||||||||||
| Sх | 0,53 | Sу | 0,61 | Sху | 0,23 | ||||||||
| Уравнение модели: y* (x) = 0,8 x + 1,2 | |||||||||||||
| Параметры линейной регрессии | Оценка значимости | Вывод | |||||||||||
| rxy | 0,69 | sr | 0,122 | t расч | 5,66 | tкр (35; 0,05) | 2,03 | средняя прямая зависимость; значимый | |||||
| q | 0,47 | a | 0,514 | g | 0,95 | zg | 1,96 | длина ДИ равна 0,36 | |||||
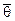
| 0,83 | b | 1,186 | ||||||||||
| se2 | 0,197 | > 20% | |||||||||||
| a | 0,8 | sa | 0,14 | Т a | 5,66 | tкр (35; 0,05) | 2,03 | значимый | |||||
| b | 1,2 | sb | 1,31 | T b | 0,92 | tкр (35; 0,05) | 2,03 | незначимый | |||||
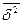
| 0,18 | F * | 32,47 | Fтабл (1; 35; 0,05) | 4,12 | адекватна | |||||||
| 0,20 | ||||||||||||
| h 2 y(x) | 0,48 | h 2 y(x) – r 2 xy | 0,0037 | 0,1 | несущественное | ||||||||
| se | 0,44 | Sу | 0,61 | 0,67 Sу | 0,41 | se > 0,67 Sу | |||||||
| Модель среднего качества и требует дополнительного уточнения. Несмотря на адекватность и значимость основного коэффициента регрессии, дисперсии, описываемой моделью, недостаточно. Незначим свободный член уравнения регрессии и стандартная ошибка модели (0,44 оС) превышает допустимую (0,41 оС). Поскольку коэффициент детерминации < 0.7, то точность аппроксимации недостаточна и модель требует улучшения. | |||||||||||||
Задание 4
