Задача №1
Колебание происходит по закону Х = Аsin3wt. Является ли оно гармоническим?
Решение
Представим данное колебание в виде набора гармоник.
Преобразуем выражение 

 ;
;
 .
.
Исходное колебание не является гармоническим, поскольку мы имеем сумму разночастотных колебаний с различными амплитудами.
Задача №2
В молекуле N2 частота колебаний атомов w0 = 4,05×1014 с-1. Масса одного атома m. Найти коэффициент k квазиупругой силы, действующей между атомами.
Решение
Положим, что при колебаниях затухания нет. Тогда собственная частота колебаний w0 = 40,45. 1014 с-1. По таблицам массу моля молекулярного азота: m = 14 г/моль. Тогда масса молекулы составит m0 = m/NA = 14/6,023.1023 = 2,32.10-26 кг (NA – число Авогадро). Полагая, что квазиупругая сила подчиняется закону Гука F = kx, для собственной частоты осциллятора имеем выражение w0 2 = k/m0. Отсюда k = m0 w0 2 = 2,32.10-26. 20.1028 = 4,04.103 Н/м.
Задача №3
Энергия частицы массой m представляет собой следующую функцию:

Найти частоту колебаний. Определить силу, действующую на частицу, при прохождении ею положения равновесия.
Определить скорость в тот момент, когда она находится в крайнем положении.
Решение
Пусть Е – энергия частицы в заданный момент времени, а Еn – потенциальная энергия в этот же момент.
 ;
;  ;
;  - положение равновесия.
- положение равновесия.
 ;
; 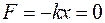
 при х = х mах.
при х = х mах.
При максимальном отклонении скорость v = 0.
 ;
; 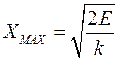 ,
, 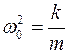 .
.
Задача №4
Сложить два одночастотных колебания, совершающихся вдоль одной прямой: а1 = 3 sin wt и а2 = 4 cos wt.
Решение.
а = а1 + а2. Преобразуем а1 к стандартному виду:
а1 = 3 sin wt = 3 cos(wt - p/2).
Для сложения одночастотных колебаний необходимо геометрически сложить векторы амплитуд повернутых друг относительно друга на 900. В результате будем иметь колебание с амплитудой F и со сдвигом фаз d: х = F cos (wt - d). Причем
 ;
;  .
.
Задача №5
Энергия резонансного перехода в ядре железа составляет 14 кэВ (1 эВ = 1,6×10-19 Дж). Добротность перехода 1010. Найти ширину спектральной линии этого мессбауэровского перехода.
Решение
Добротность  ,
,
где Е – энергия колебательной системы в данный момент вращения, DЕ – потеря энергии системой за период колебаний – это и есть ширина спектральной линии.
 ; DЕ = 1,4×10-18 Дж.
; DЕ = 1,4×10-18 Дж.
Задача №6
Рубиновый лазер излучает на l = 0,58 мкм. Ширина линии изменяется от 4,7 10-2 до 4,7 10-4 Ангстрем (А0). В каких пределах изменяется добротность лазера (резонатора Фабри-Перо)?
Решение
Добротность  , где w - частота (круговая) излучения, Dw - ширина резонансной кривой на полувысоте:
, где w - частота (круговая) излучения, Dw - ширина резонансной кривой на полувысоте:
 ;
;  ;
;
Поэтому  , l = 0,58 мкм = 5800 А.
, l = 0,58 мкм = 5800 А.
 ,
,  .
.
Задача №7
Сложить 3 одночастотных колебания, совершаемых вдоль одной прямой: Х1 = 3 sin wt; Х2 = 4 coswt; Х3 = 5cos(wt + j), где j = -arctg(3/4).
Решение
Преобразуем


Вначале сложим первые два колебания
х = х1 + х2

 ;
; 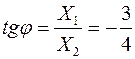 .
.
Теперь сложим эту сумму с третьим колебанием. Получим
 .
.
Задача №8
Период колебания качелей Т0. Как изменится период колебаний, если на качели сядет человек массой М. Длина качелей L 0. m0 - масса пустых качелей.
Решение
Основное уравнение динамики вращательного движения для качелей
 ;
; 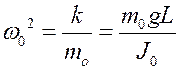 .
.
Когда на качели сел человек с моментом инерции –  , то
, то  -момент инерции всей системы
-момент инерции всей системы
L – расстояние от оси вращения до центра масс системы человек-качели.
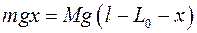 ;
; 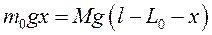 ;
;

 ;
; 






1) Первый случай (масса качелей больше массы человека):
 и
и  ;
;  ,
,

2) Второй случай (масса качелей меньше массы человека):


Задача №9
Самолет стартует под углом α к горизонту с ускорением а. Найти частоту малых колебаний математического маятника длины l подвешенного в самолете.
Решение
Найдем эквивалентное ускорение g1 обусловленное инерционными силами и силой тяжести. Из рисунка по теореме косинусов
(g1)2 = а2 + g2 + 2аg sin α
ω2 = g1 /l





Задача №10
В электрическом колебательном контуре индуктивность катушки равна 4.10-3 Гн, а максимальный ток в ней 0,1 А. В момент, когда ток в катушке равен 0,05 А, определить энергию электрического поля конденсатора.
Решение
Мгновенное значение тока i = Imaxsin (wt) Мгновенное значение эдс индукции в катушке e = L i1(t) = L Imaxw cos (wt) равно напряжению на конденсаторе. Определим sin (wt) из первого выражения, подставив i и Imax, и найдем cos (wt)= 31/2/2. Собственная частота контура w2 = LC, где С – емкость конденсатора. Тогда энергия электрического поля в конденсаторе Е = Ce2/2 = 1,5.10-5 Дж.
Задача №11
Колебательный контур содержит конденсатор емкостью С = 1,2 нФ и катушку индуктивности L = 6 мГн. Активное сопротивление R = 0,5 Ом. Какую среднюю мощность должен потреблять такой контур, чтобы в нем поддерживались незатухающие колебания с амплитудой напряжения на конденсаторе UM = 10 В?
Решение
Резонансная частота контура находится по формуле

 .
.
Добротность связана с резонансной частотой и коэффициентом затухания b соотношением
Q = wр/(2b) =  , b = R/L,
, b = R/L,
а так же с убылью энергии DЕ за период
Q/2p = E/DE, dE = 2pЕ/Q.
Энергия, накопленная в конденсаторе E = C  /2 и потребляемая мощность
/2 и потребляемая мощность
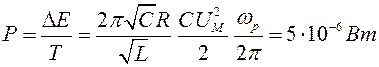
Задача
Коаксиальный кабель состоит из центральной части (жилы) диаметром d и проводящей оплетки диаметром D. Пространство между жилой и оплеткой заполнено диэлектриком с диэлектрической проницательностью ε. Найти ёмкость и индуктивность в расчёте на 1 метр длины для такого кабеля.
Решение.
Начнем с определения ёмкости куска кабеля длины l, считая его бесконечно длинным и прямым. Зарядим центральную проводящую жилу и оплетку равными по величине и противоположными по знаку зарядами: q = ρl и – q, где ρ – линейная плотность заряда на жиле. Напряженность поля в диэлектрике на расстоянии r от оси равна
 .
.
Разность потенциалов между жилой и оплеткой:
 .
.
Емкость на один метр длины (l = 1 м)
 .
.
Определим индуктивность. Для этого используем два выражения для энергии магнитного поля в объёме ΔV:
 и
и  .
.
Итак, пусть по проводящей жиле течет ток I, а по оплетке – такой же ток в противоположном направлении. Тогда индукция магнитного поля снаружи кабеля будет нулевой, а внутри объема заполненного диэлектриком на расстоянии r от оси кабеля
 .
.
Возьмем в этом диэлектрике тонкий цилиндрический спой радиуса r и толщины dr с длиной l. Энергия магнитного поля в выделенном объеме равна
 .
.
Тогда энергия во всем зазоре между жилой и оплеткой определяется интегрированием
 .
.
На основании изложенного выше индуктивность кабеля длины l будет равна
 .
.
Можно вычислить волновое сопротивление кабеля по формуле  . Это чисто активное сопротивление. Если к концу куска кабеля подключить резистор такой величины, то от конца кабеля не будет происходить отражения электромагнитной волны, бегущей вдоль него.
. Это чисто активное сопротивление. Если к концу куска кабеля подключить резистор такой величины, то от конца кабеля не будет происходить отражения электромагнитной волны, бегущей вдоль него.






