Задача №23
На гладкой ровной поверхности стола лежит тонкий однородный стержень массой m и длиной L. На конец стержня, перпендикулярно его оси действует импульс силы F, направленный горизонтально. На какое расстояние передвинется центр масс стержня за время поворота? Чему равны энергии поступательного и вращательного движения стержня и его полная энергия после воздействия импульса силы? Трением пренебречь.
Решение
На систему подействовал импульс внешней силы и изменил движение. Импульс силы равен изменению импульса тела. Под действием импульса силы центр масс тела приобрёл скорость v. Пусть ω = dφ/ dt -угловая скорость вращения относительно ц. м.
импульс силы.
Момент силы 
, 
(применяем основное уравнение динамики вращательного движения)
Стержень однородный, вращается относительно середины, поэтому момент инерции равен
.
Задача.
Гладкий стержень свободно вращается в горизонтальной плоскости с угловой скоростью w0 вокруг неподвижной вертикальной оси О, относительно которой его момент инерции равен J. На стержне около оси вращения находится небольшая муфта массой m соединённая с этой осью нитью. После пережигания нити муфта начинает скользить вдоль стержня. Найти скорость v’ муфты относительно стержня в зависимости от её расстояния r до оси вращения.
Решение
Сохраняется кинетическая энергия:
(1)
и сохраняется момент импульса:
Jw0 = (J + mr2) w (2)
v2 = (v¢)2 + (w r)2 (3)
wr - скорость переносного движения
v’ - скорость муфты относительно стержня
v - полная скорость муфты относительно земли.
Задача.
На жёстком проволочном полукольце радиуса r0 которое может свободно вращаться вокруг вертикальной оси AB, находятся две одинаковые небольшие муфточки. Их соединили нитью и установили в положение 1-1. Затем всей установке сообщили угловую скорость w0 и, представив её самой себе, пережгли нить в точке А. Считается, что масса установки сосредоточена в муфточках, найти её угловую скорость в момент, когда муфточки без трения соскользнут в крайнее положение 2-2.
Решение:
r2w2 – r02w02 = 2gh (1)
закон сохранения
D(Eкин) = mgh; v = wr
В горизонтальной плоскости силы не действует и момент жидкости сохраняется.
L1 – момент оси тяжести (в горизонтальной плоскости)
L = mvr = mwr2=Jw; J – момент инерции
r2w = r02w (2)
r02 = r2 + h2 (3)
Задача №24
На неподвижное тело массой 12 кг в течение времени t действует сила F = F0e--at , где F0 = 10H, a = 2с—1.
Определить скорость движения тела после действия силы в течение времени τ.
Решение
mvK= 
- импульс тела при переменной во времени силе
F = F0 e--at
mvK= 
= 
F0e--atdt= 
e--atdt(-at)=
= e--at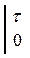 
= (e--at -1)
Задача №25
На наклонной плоскости составляющей угол a с горизонтом лежит материальная точка. Ей щелчком сообщают вдоль плоскости горизонтальную скорость u0. Через какое время материальная точка остановится, если коэффициент трения о плоскость m > tga.
Решение
Угол между ОХ и скоростью u в некоторый момент времени равен b
 |
В горизонтальной плоскости действует скатывающая сила FZ = mg×sina и сила трения F = mmg cosa. За время Dt импульс материальной точки изменится на mdu =ΣFiΔt.
Проекция силы трения на ось Х составит: FТРХ = -m mg cosa sinb, а проекция скорости - dv = d (v sinb)
В проекции на ось Х изменение импульса запишем в виде
md (v sinb) = (-FТР sinb + FСК) dt
Проектируем уравнение импульсов на направление касательной к скорости: mdv = (-mmg cosa + mg sina sinb) dt = (-FТР +FСК sinb)dt.
Заметим, что
; 
.
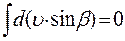Разделим обе части уравнения на FСК и FТР соответственно и сложим
= 
+ 
= 
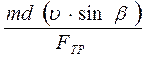dt = 
+ 
t= 
= 
(-v0)+ 
´
´ 
= 
= 
Задача №26
По тонкому стержню, покоящемуся на гладком столе производится в некоторой точке А удар с силой F1.
1) Показать, что в момент удара стержень вращается около вертикальной оси проходящей через точку О. Причём, если трение пренебрежимо мало, то АС*ОС = Jс/M = S1S2 , Jс - момент инерции стержня относительно оси, проходящей через центр масс, M – масса стержня, S1 и S2 расстояния от точек 
и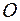 
до точки 
.
2) Что произойдёт, если ударить по стержню в точке О? Где будет проходить ось вращения?
3) Что произойдёт, если ударить по самому концу стержня?
Решение
Приложим мысленно в точке С (в центре масс) две равные и противоположные силы F1 и F2, сумма которых равна нулю. При этом сила F1 по величине и направлению равна силе удара. Но теперь сила F1, проходящая через ц.м., . вызовет поступательное движение стержня с ускорением а = F1/M, а под действием пары сил F1 и F2 будет происходить вращение с угловым ускорением 
около оси, проходящей через центр масс С. Вследствие вращения стержня точка О должна бы двигаться с линейным ускорением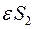 
, но если точка О покоится, то 
. Имеем
; 
.
Задача №27
На стоящий на гладкой горизонтальной поверхности клин массой М падает шар массой m и отскакивает в горизонтальном направлении. Найти горизонтальную проекцию скорости клина nx. Будем считать, что после удара движение происходит без трения, удар – абсолютно упругий.
Решение
За время удара импульс силы тяжести пренебрежительно мал, поэтому мы можем записать закон сохранения энергии и закон сохранения импульса системы шарик - клин в проекциях на оси ОХ и ОУ (горизонтальную и вертикальную соответственно).
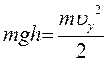
V – скорость клина, М – его масса
Начальная энергия шарика равна mgh
.
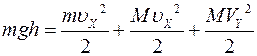Единственная сила, которая может изменить импульс силы, это сила тяжести, но она не успевает это сделать. (Если шарик попадёт в ц.м., то вращения не будет, в остальных случаях будет добавляться вращение).
.
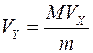
Задача №28
Из пушки соскальзывающей по наклонной плоскости без трения и прошедшей путь L, производится выстрел в горизонтальном направлении. При какой скорости снаряда пушка остановится после выстрела?
Решение
В момент выстрела импульс силы тяжести намного меньше импульса силы реакции, т.е. импульс системы пушка – снаряд будет сохраняться в направлении перпендикулярном силе реакции наклонной плоскости, т.е. вдоль наклонной плоскости. Ось Х направим вдоль наклонной плоскости вниз.
m – масса снаряда, М – масса пушки, v0 – скорость пушки в момент выстрела;
u0 можно найти из закона сохранения энергии.
; 
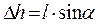
проекция горизонтальной скорости снаряда Vc на ОХ:
Импульс снаряда по оси Х
.
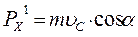
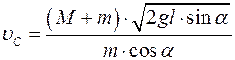
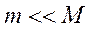
Задача №29
Мешок с мукой скользит без начальной скорости по гладкой доске под углом 60° к горизонту. После спуска мешок падает на шероховатый пол с коэффициентом трения m = 0,7. Где остановится мешок?
Решение
Пусть масса мешка m, тогда из закона сохранения энергии для движения мешка по наклонной плоскости с высоты h имеем скорость мешка в момент удара о пол
Удар мешка в пол неупругий. Пусть N - сила реакции, возникающая при ударе мешка о пол. Импульс силы N - компенсирует вертикальную составляющую импульса мешка.
Мешок дальше двигаться не будет и остановится у подножия наклонной плоскости.
Задача №30
На наклонной плоскости с углом a находится скатывающееся тело, радиус которого R, момент инерции J, масса тела М. Найти ускорение центра масс (ц.м.) тела при скатывании и силу трения. Проскальзывания нет.
Решение
Пусть R - сила реакции. Момент N вокруг мгновенного центра вращения А (точка контакта тела с наклонной плоскостью) создаёт только сила тяжести mg с плечом АD
по теореме Штейнера (Jc – момент инерции тела вокруг оси, проходящей через центр масс)
; JAe = mgr sina; 
;
Для нахождения силы трения необходимо записать второй закон Ньютона для движения центра масс. В проекции на направление движения имеем
mac = mg sin a - Fтр.
Отсюда и находим Fтр.
Другие способы решения этой задачи см. И.В. Савельев. Курс общей физики, т. 1, § 41
Задача №31
В каком случае энергия запасённая в пружине больше, когда она деформирована от Х0 на DХ, или от Х0 + DХ на DХ.
Решение
; 
;
.
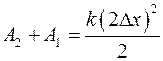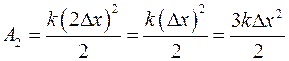Во втором случае энергии запасено больше в 3 раза.
Задача №32
Какую форму должна иметь однородная вертикальная колонна с круглым поперечным сечением, чтобы в её произвольном горизонтальном сечении, давление создаваемое грузом массой m помещённом на верхнем основании и собственным весом колонны было одинаковым, Плотность материала колонны r, радиус её верхнего основания r.
Решение
Ось Y направим горизонтально, ось Х вертикально вниз. Пусть уравнение образующей 
, тогда объем тела вращения (колонны) 
.
Давление в любом сечении 
,
или
.
Здесь справа стоит выражение для давления груза на верхнее основание. Преобразуем данное выражение
.
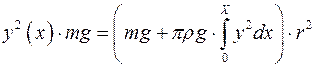Продифференцируем обе части по х.
;
; 
; 
;
; 
.
С – постоянная интегрирования
Используя начальные условия при X = 0, Y = r, получим:
,
Задача №33
Определить время опорожнения конической воронки с углом при вершине 2a, заполненной водой, если отверстие, через которое вытекает вода, имеет площадь S, высота уровня воды до отверстия h.
Решение
Радиус верхней поверхности воды в воронке есть функция высоты уровня воды 
, площадь этой поверхности 
.
Если вода вытекает без трения, то сохраняется механическая энергия воды 
; отсюда 
;
Объем воды, вытекающий за время dt, определенный по верхнему уровню: dV = Sdh = pr2 dh; 
.
Объем воды, вытекающий за это же время через нижнее отверстие
dV = S0 vdt, следовательно
pf2(h)dh = S0 (2gh)1/2dt
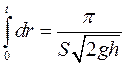
(1)
Систему координат выбираем связанной с верхним уровнем воды и записываем уравнение образующей конуса
X0 = 0, X1 = H,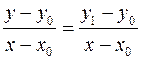 
;
Y0 = R, Y1 = r0
, 
,
,
где 
; 
Теперь вычислим интеграл в правой части (1), представив его в виде суммы интегралов J1, J2, J3:
; 
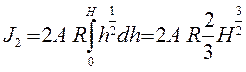Обращаясь к (1), имеем
,
, 
.
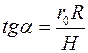Задача №34.
Гиря массой m = 32 кг подвешена к балке на двух канатах L1 = 3м, L2 = 4м. Расстояние между точками подвеса L3 = 3м. Найти силу натяжения канатов.
Решение
Условие равновесия гири: 
Проектируем это векторное равенство на оси x и y:
Возводим в квадрат и складываем. Из геометрии имеем
; 
;
; 
;
;
; 
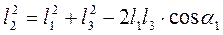Вывод:
Силы натяжения канатов не зависят ни от упругих свойств канатов, ни от геометрических размеров этих канатов.
Задача №35
Тело массой m подвешено на 3-х канатах симметрично. Центральный канат длиной L1 имеет модуль Юнга Е1 и поперечное сечение S1. Боковые канаты одинаковы и характеризуются величинами L2, Е2, S2. Найти натяжение канатов.
Решение
Предыдущая задача свелась к разложению вектора mg по двум векторам, направленным по канатам. Эта задача решается однозначно. Задача разложения вектора mg по 3-м направлениям не может быть решена однозначно без дополнительных соображений, например, без учёта деформаций.
; 
; 
; 
;
; 
;
; 
;
.
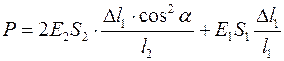Вывод:
Силы натяжения канатов зависит как от геометрических характеристик, так и от физических характеристик материала канатов.
Задача №36
Стальная балка длиной 1м, зажата между вертикальными опорами так, что не может деформироваться. Определить силу упругости, возникающую в балке, при её нагревании на 30°С. Определить величину упругой энергии накопленной в балке.
Решение.
Имеет место тепловое расширение
; 
;
α – коэффициент теплового расширения материала
Считаем, что при расширении справедлив закон Гука
; 
Е – модуль Юнга.
Преобразуя, получим
F = 10×10-4×30×1010×30×20×1010×13×10-6 = 9×104H
Для вычисления энергии используем формулу
, где k = 
.
Задача №37
Три точки массами m1, m2, m3, расположены в углах треугольника. Найти положение центра тяжести. Решить эту же задачу для треугольной пластины, для треугольника из стержней массами m1, m2, m3 (см. таблицу «Центры масс»).
Решение
y
x
Первый способ:
