Задача №1
Шар массой m1 = 5 кг движется со скоростью V1 = 1 м/с и сталкивается с неподвижным шаром массой m2 = 2 кг. Определить скорость u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
v1


 m1 m2
m1 m2
 |  |  |  |  |  |  |

Решение.
Поскольку удар прямой и центральный, то после удара шары не изменяют состояния вращения и движутся по одной прямой. Поскольку удар абсолютно упругий, то выполняется закон сохранения энергии, в данном случае кинетической.
Справедлив также закон сохранения импульса:
 (1)
(1)
Начальный импульс системы до удара:  , т.к. второй шар покоится. После удара:
, т.к. второй шар покоится. После удара: 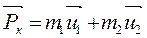 .
.
Проектируем (1) на направление удара:
m1V1 = m1u1 + m2u2 (2)
Закон сохранения энергии:
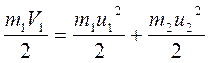 ` (3)
` (3)
Решая совместно (2) и (3), находим u1 и u2.
Задача №2
Блок, имеющий форму диска массой m = 0,4 кг, вращается под действием силы натяжения перекинутой через него нити, к концам которой подвешены грузы массами m1 = 0,3 кг и m2 = 0,7 кг. Определить силы натяжения Т1 и Т2 нити по обе стороны блока и силу давления блока на ось.
 |
 m
m
 | |||||||
 | |||||||
 | |||||||
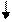 | |||||||
 m1
m1
m2
Решение.
На груз действуют силы тяжести и силы натяжения нитей. Поэтому уравнение движения грузов заключается как уравнение поступательного движения:
Т1 – mg = m1a, (1)
m2g – T2 = m2a, (2)
знаки расставлены с учетом направления движения.
Блок приходит во вращательное движение под действием моментов сил натяжения нитей Т1 и Т2. Силы натяжения Т1 и Т1|; Т2 и Т2| равны по модулю, т.к. нить считается не имеющей массы. Плечо сил Т1| и Т2| равно радиусу блока. Поэтому основное уравнение динамики вращательного движения для блока имеет вид:
Ie = Т2|R- Т1|; |Т1|| = |Т1| и |Т2| = |Т2||; (3)
где I – момент инерции блока (диска)
 ;
;
e - угловое ускорение, связанное с линейным ускорением а зависимостью (проскальзывания нити по блоку нет):
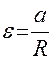 .
.
Подставим I и e в (3):
 ; или
; или  ; (4)
; (4)
Для нахождения натяжения нитей необходимо решить систему уравнений (1), (2) и (4), в которых неизвестно а.
Сложим (1) и (2):

и подставим это выражение в (4):
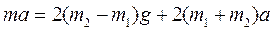 .
.
Найдем отсюда а:
 .
.
Из (1) находим Т1
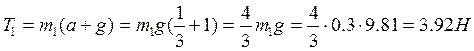
Из (2) находим Т2

Силу, давления на ось определим из равенства:
N = T1 + T2 + mg:
Ответ: Т1 = 3,92 Н; Т2 = 4,58 Н.
Задача №3
Зависимость скорости материальной точки от времени представлена на графике. Найти и изобразить зависимость всех кинематических величин, описывающих движение, от времени.
Решение.
Зависимость представлена графиком
0 - t1 – равноускоренное движение 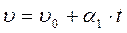 , ускорение
, ускорение 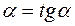 ;
;
t1 - t2 – равномерное движение вдоль прямой  ;
;
t2 - t – равнозамедленное движение  .
.
Рассмотрим перемещения. При одномерном движении перемещение и координата тождественны и нет нужды вводить вектор.
 - общая формула для перемещения при равнопеременном движении. Для правильного применения формулы необходимо соблюдать правило знаков:
- общая формула для перемещения при равнопеременном движении. Для правильного применения формулы необходимо соблюдать правило знаков:
Выбираем ось Х, задаём векторы начальной скорости и скорости ускорения. Если направление скорости совпадает с направлением оси ОХ, то знак перед скоростью берём (+), если нет - (-). То же самое относительно ускорения.
Запишем закон перемещения материальной точки на участке 0 - t1: 
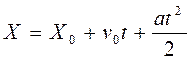 X0 - начальная координата точки из графика не находится, поэтому эта величина должна быть задана дополнительно. Пусть Х0 задано и является отрицательным числом. В момент t будем считать
X0 - начальная координата точки из графика не находится, поэтому эта величина должна быть задана дополнительно. Пусть Х0 задано и является отрицательным числом. В момент t будем считать 
На промежутке t1 - t2: Х = Х0 + u t т.к. а = 0


 - линейная зависимость от времени
- линейная зависимость от времени
t > t2, равнозамедленное движение:
 -параболическая зависимость от времени.
-параболическая зависимость от времени.
По графику  строим график Х(t). Вершина параболы будет в той точке t, в которой
строим график Х(t). Вершина параболы будет в той точке t, в которой 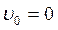 . Это точка t4.
. Это точка t4.
 т.к. скорость это производная от перемещения по времени. Движение равнозамедленное, значит график - парабола, ветви направлены вниз, вершина там, где u = 0 т.е. в t3
т.к. скорость это производная от перемещения по времени. Движение равнозамедленное, значит график - парабола, ветви направлены вниз, вершина там, где u = 0 т.е. в t3

Построим график зависимости а(t)
В t1 и t2 ускорение не определяется, т.к. невозможно провести касательную к графику скорости в этих точках, поскольку ускорение невозможно поменять мгновенно, как и скорость.
Геометрический смысл перемещения на графике u(t).
Если функция гладкая, то с заданной точностью её всегда можно представить в виде отрезков прямых, ломанных или ступенчатых.
Но такие ступеньки представляют собой график равномерного движения, то тогда  , но на этом графике
, но на этом графике 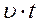 - это площадь соответствующего прямоугольника. Таким образом, геометрический смысл перемещения материальной точки - площадь под кривой на графике u(t).
- это площадь соответствующего прямоугольника. Таким образом, геометрический смысл перемещения материальной точки - площадь под кривой на графике u(t).
Аналогично, т.к. u = at, то геометрический смысл скорости на графике a(t) это тоже площадь под кривой a(t), т.к. движение с произвольным ускорением с заданной наперед степенью точности можно представить как движение с постоянным ускорением на отдельных элементарных участках.
Вернёмся к графику u(t). Видно, что в момент t4 u = 0, а затем поменяла знак, следовательно, перемещение может быть равно 0 как и в задаче, значит мы обязаны считать площадь S1 со знаком плюс, где v(t) > 0. S2 со знаком минус, где v(t) < 0, но тогда перемещение за время Т


Путь, пройденный материальной точкой – еще одна кинематическая характеристика движения. По определению, путь – это длина траектории, повторенная столько раз, сколько раз по траектории проследовала материальная точка. Из определения следуют свойства пути:
а) путь, всегда скалярная положительная величина;
б) путь может только нарастать со временем.
График зависимости пути от времени получается из графика зависимости перемещения от времени путем смещения оси времени t вверх или вниз с тем, чтобы путь S при t = 0 также равнялся нулю. Кроме того функцию S(t) необходимо сделать нарастающей. Для этого спадающие вниз ветви функции перемещения х(t) (у нас - параболы) необходимо отразить от горизонтальной оси t так, чтобы они стали нарастающими (см. рис. на обложке).
На графике v(t) всегда справедливо, что
S(t) = |S1(t1¸t2)| + |S2(t2¸t3)| + … + |Sn(tn-1¸tn)|.
 .
.
График зависимости ускорения от времени строится аналогичным образом. В тех точках, где график скорости претерпевает излом, ускорение не определено. Следовательно, движение нашим графиком v(t) задается не вполне корректно.

Задача №4
Движение тела брошенного под углом к горизонту.
Рассмотрим движение материальной точки (м.т.) в однородном гравитационном поле, т.е. в таком, в котором в любой точке пространства вектор ускорения свободного падения  одинаков и по величине, и по направлению. Пусть м.т. начинает движение из начала координат со скоростью u0 под углом к горизонту a0 (ось х), а вектор
одинаков и по величине, и по направлению. Пусть м.т. начинает движение из начала координат со скоростью u0 под углом к горизонту a0 (ось х), а вектор  направлен вертикально вниз (ось у – направлена вверх). Это движение не по одной прямой и не по окружности, но это движение в плоскости. Для решения таких задач, как и в общем случае, используется принцип независимости движений. В нашем случае это сложное плоское движение можно представить как результат сложения двух движений: равномерного прямолинейного движения вдоль оси х и равнопеременного движения вдоль оси у. Такое представление возможно потому, что это движение описывается вектором перемещения (или радиус-вектором), а любой вектор можно разложить по любым двум произвольным направлениям.
направлен вертикально вниз (ось у – направлена вверх). Это движение не по одной прямой и не по окружности, но это движение в плоскости. Для решения таких задач, как и в общем случае, используется принцип независимости движений. В нашем случае это сложное плоское движение можно представить как результат сложения двух движений: равномерного прямолинейного движения вдоль оси х и равнопеременного движения вдоль оси у. Такое представление возможно потому, что это движение описывается вектором перемещения (или радиус-вектором), а любой вектор можно разложить по любым двум произвольным направлениям.

Запишем закон равномерного движения по оси х.
 (1)
(1)
 (2)
(2)
По оси у закон равнопеременного движения имеет вид:
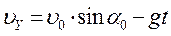 (3)
(3)
 (4)
(4)
Прежде всего, определим время подъёма тела на максимальную высоту. Очевидно, тело будет подниматься до тех пор, пока Vy не обратится в нуль, т.е.
 ;
;  – время подъема;
– время подъема;
 (5)
(5)
Можно показать, что время спуска будет таким же. Тогда полное время движения будет равно.
 .
.
За время t подъёма, тело поднимется на Y(под)
 (6)
(6)
Дальность полёта
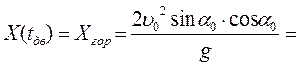
 (7)
(7)
из формул (6) и (7) вытекает, что максимальная высота подъёма Н будет при угле бросания 90° и составит
 (8)
(8)
Максимальная дальность полёта будет при угле бросания 45°, и составит x 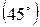 =
= 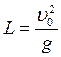
Как видим, максимальная возможная дальность полёта в два раза больше максимальной высоты подъёма при заданной начальной скорости nо.
Для произвольного угла бросания:
 (9)
(9)
Рассмотрим скорость м.т. в произвольной точке траектории.
По теореме Пифагора:

 (10)
(10)
Угол a, который вектор скорости составляет с осью х, находим из соотношения:
 (11)
(11)
Рассмотрим ускорения.
Проектируем вектор ускорения свободного падения 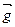 , на направление вектора скорости и на направление перпендикулярное ему
, на направление вектора скорости и на направление перпендикулярное ему
an = g cosa; at = g sina, но an = n2/R,
где R – радиус кривизны траектории в момент времени t, т.е. в данной точке траектории:
 . (12)
. (12)
Траектория точки – парабола (см. задачу № 6). Для нас важнейшим моментом в приложениях (например, в оптике) является кривизна параболы в ее вершине. Для вершины: a = 0;
 тогда
тогда  . (13)
. (13)
Задача №5
Шарик, посаженый на один конец невесомой жёсткой спицы длины L, вращается в горизонтальной плоскости вокруг его другого закреплённого конца. Начальная скорость шарика u0, коэффициент трения m. Сколько оборотов n сделает шарик до остановки и сколько времени  он будет вращаться, если вращение равнозамедленное? Каково полное ускорение шарика в момент, когда он сделает один оборот?
он будет вращаться, если вращение равнозамедленное? Каково полное ускорение шарика в момент, когда он сделает один оборот?
Решение.
Для определения числа оборотов воспользуемся законом сохранения энергии. Первоначальный запас кинетической энергии идёт на работу против сил трения Fтр. Используем определение работы силы через изменение энергии

где S- путь, пройденный шариком до остановки. Отсюда 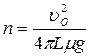
У нас равнозамедленное движение (вращение), значит, угол поворота изменяется со временем по закону:
 , а угловая скорость
, а угловая скорость  ; ε – угловое ускорение. По истечении времени
; ε – угловое ускорение. По истечении времени  вращение прекращается:
вращение прекращается:


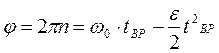
Рассмотрим полное ускорение после первого оборота.
Такое ускорение состоит из тангенциального и нормального ускорения. Нормальное ускорение направлено к центру вращения (к центру кривизны) и вычисляется по формулам:
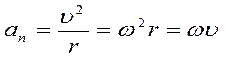 (r = L)
(r = L)
Для того чтобы найти нормальное ускорение необходимо знать линейную скорость шарика после первого оборота 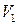 . Найдём её из закона сохранения энергии:
. Найдём её из закона сохранения энергии:
 ;
; 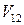 =
= 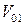 - 4mgpL ³ 0.
- 4mgpL ³ 0.
Отсюда  .
.
тангенциальное ускорение аt = eL.
Поэтому искомое полное ускорение а находим из:
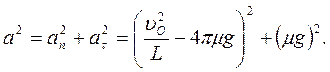
Задача
Определить длину пробега самолета после посадки, если посадочная скорость равна uпос., а сила сопротивления пропорциональна силе тяжести. Принять, что коэффициент сопротивления m состоит из следующих составляющих:
m = mср. аэр + mср. тор + mср. т.п + mср. рев,
где
mср. аэр - средний коэффициент аэродинамического сопротивления самолета при разбеге или пробеге, равный 0,05 – 0,08;
mср. тор - средний коэффициент трения качения колес шасси при использовании колесных тормозов. При торможении на бетонной полосе 0,20 – 0,25. При торможении на грунте 0,10 – 0, 15;
mср. т.п - средний коэффициент аэродинамического сопротивления тормозного парашюта, используемого при посадке. У существующих тормозных парашютов 0,10 – 0, 15;
mср. рев - средний коэффициент сопротивления движению самолета при использовании реверса тяги двигателей. Величина этого коэффициента зависит от значения отрицательной, реверсивной тяги двигателей 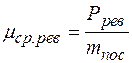 .
.
Решение.
Исходим из закона сохранения энергии. Изменение кинетической энергии равно работе сил сопротивления Fc на длине пробега L:
 ;
;  , отсюда
, отсюда  .
.
Задача №6
Цель находится на расстоянии L от мяча на вышке высотой H. Под каким углом aо необходимо запустить мяч с поверхности земли, чтобы поразить цель? Начальная скорость мяча  .
.
Решение.
Пусть мяч находится на земле на расстоянии L от вышки высотой Н, где располагается цель. Задача - поразить цель. Найти траекторию, значит связать х и у. Для этого из  выразим время и подставим в
выразим время и подставим в  получим:
получим:
 ,
, 

Получаем:
Отсюда найдём угол  , под которым нужно бросить мяч со скоростью n.
, под которым нужно бросить мяч со скоростью n.
 ,
, 
Поскольку дискриминант может быть отрицательным, то это означает, что при заданных a0 и v0 не всякая цель может быть поражена, т.е. существует какая-то линия безопасности, за пределы которой мяч попасть не может. Эта линия связывает допустимые значения L1 от Н1 и находится из условия D = 0.

 ,
, 
- уравнение параболы безопасности.
В пространстве совокупность таких линий образует параболоид безопасности.
Если Н 1 = 0, то это выражение задает максимальную дальность полёта.
Уравнение (1) при положительном дискриминанте имеет два решения для углов. Это говорит о том, что любая точка, лежащая внутри параболы безопасности при заданной начальной скорости u0 может быть достигнута при двух различных углах: при навесной и настильной траектории. Точки, лежащие на траектории безопасности, достигают только при одном значении a0, т.к. в этом случае уравнение (1) имеет один корень.
Задача №7
Найти относительную скорость движения двух снарядов выпущенных со скоростями  и
и  под углами a1 и a2 к горизонту. Показать, что относительная скорость не меняется с течением времени.
под углами a1 и a2 к горизонту. Показать, что относительная скорость не меняется с течением времени.
Решение
По определению  . Спроектируем это равенство на горизонтальную и вертикальную оси:
. Спроектируем это равенство на горизонтальную и вертикальную оси:


Оба эти выражения не зависят от времени, следовательно, и величина вектора nотн не зависит от времени.
Задача №8
Показать, что максимальная дальность полёта снаряда, выпущенного из пушки с  под углом
под углом 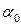 к горизонту с обрыва, высотой Н меньше 45°. Вывести соответствующие формулы.
к горизонту с обрыва, высотой Н меньше 45°. Вывести соответствующие формулы.

Решение
Решение задачи производим на основе решения предыдущих задач
 |
 ;
; 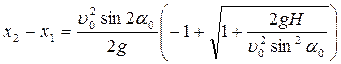
 |
Непосредственно на вопрос задачи дают ответ следующие соотношения:
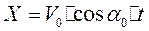 ,
, 
Исключив из этих уравнений время t и положив y = H, x = L, получим

При условии, что подкоренное выражение положительно, имеем:
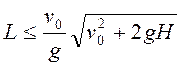


Для максимальной дальности полета в неравенстве следует взять знак “равно”. Тогда
 , следовательно, угол бросания меньше 450.
, следовательно, угол бросания меньше 450.
Задача №9
Динамометр находится на гладкой горизонтальной поверхности. К одному концу приложена сила F1, к другому - сила F2. Пружина прикреплена к динамометру массой М и к крюку массой m. Массой пружины пренебречь. Определить показания динамометра.
Решение
Динамометр показывает силу деформации пружины.
Пусть:
Т1 – сила, с которой пружина действует на крюк.






