Т2 – сила, действует со стороны пружины на корпус динамометра.
Для движения корпуса второй закон Ньютона запишем в виде 
Уравнение движения для крюка: 
Уравнение движения для пружины  т.к. Mпр = 0. Мпр – масса пружины. Следовательно
т.к. Mпр = 0. Мпр – масса пружины. Следовательно
 .
.
Динамометр покажет силу Т  .
.
Если масса крюка равна нулю, то T = F. Если масса крюка М равна массе корпуса  .
.
Если  , значит, динамометр привязан, тогда
, значит, динамометр привязан, тогда 
Если сумма сил действующих на систему – корпус, крюк, пружина не равна нулю, то вся система будет двигаться с ускорением а.
Задача №10
Дана длина l коромысла неравноплечих весов и его масса m. На концах коромысла подвешены грузы массами М 1 и М2, найти положение центра масс.
Решение.
Пусть m – масса коромысла, а m1 = m/l – масса единицы длины коромысла.

Уравнение моментов сил относительно точки О:
.
Отсюда 
Задача №11
Найти изменение импульса самолета, выполняющего петлю Нестерова радиуса R, за 1/2 периода обращения, если его линейная скорость u, масса m.
Решение
Изобразим импульсы самолета в рассматриваемых точках

относительно заданной оси х. Изменение импульса за полпериода
 .
.
Проектируем это векторное равенство на ось х.
DPх= -mv – mv = -2mv
Задача №12
Самолет массой m, выполняя петлю Нестерова, движется по окружности радиуса R с постоянной по модулю скоростью u0.
Найти среднее за полпериода значение результирующих всех сил, приложенных к самолету (см. предыдущую задачу).
Решение
Сила, действующая на самолет, искривляет его траекторию, остается неизменной по величине, но изменяется по направлению, т.е. зависит от угла α. Поэтому, применяя теорему об изменении импульса материальной точки под действием переменной силы, имеем:
 ,
,
Т - период обращения самолета






Задача №13
Расход жидкости по трубе составляет Gv = 20 л/сек. Труба изогнута под прямым углом. Найти величину и направление силы, действующей на трубу. Плотность жидкости r = 0,83 г/см3, сечение трубы S = 5 см2.
Решение.
Поток жидкости меняет направление, следовательно, изменяется импульс выделенной массы жидкости, проходящей изгиб, что возможно только под воздействием сил, действующих на жидкость со стороны трубы. По третьему закону Ньютона, точно такой же импульс, а, значит, и сила, будет действовать на трубу со стороны жидкости.
Выделенное сечение трубы за время dt успеют пройти лишь те частицы, которые находятся от него на расстоянии udt, т.е. за время dt через сечение трубы пройдёт объем

 расход жидкости объемный
расход жидкости объемный

По второму закону Ньютона в интегральной форме
 ,
,
или
 .
.

 Учтем, что |PH| = |PK| =P
Учтем, что |PH| = |PK| =P
 - ее импульс; m – выделенная масса жидкости, проходящая через сечение трубы за время Dt
- ее импульс; m – выделенная масса жидкости, проходящая через сечение трубы за время Dt
 разделим правую и левую части на t,
разделим правую и левую части на t,

 - массовый расход жидкости; V – объем жидкости.
- массовый расход жидкости; V – объем жидкости.



 ;
; 
Из чертежа  ;
;  ;
;
Окончательно имеем:


Задача №14
Стальной шарик скользит без трения по гладкому полу и налетает на препятствие из стали. Каким должен быть угол падения j, чтобы шарик отскочил перпендикулярно к плоскости препятствия, если коэффициент трения между шариком и препятствием равен m.
Решение.

Пусть Dt – время соударения. Изменение импульса за время соударения
 . F – сила, действующая на шарик со стороны препятствия. Проектируем это векторное равенство на оси х и у.
. F – сила, действующая на шарик со стороны препятствия. Проектируем это векторное равенство на оси х и у.

 .
.
По условию:




В последнем соотношении надо взять знак «-», т.к. конечная скорость шарика направлена против оси х.


 - нормальная реакция препятствия.
- нормальная реакция препятствия. 
 (1)
(1)
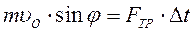 (2)
(2)
 - формула, задающая силу трения скольжения как предельное значение силы трения покоя. Разделим (1) на (2):
- формула, задающая силу трения скольжения как предельное значение силы трения покоя. Разделим (1) на (2):

Отсюда:

Выясним, при каких условиях возможно такое соударение. Поскольку
 , то
, то  ; и tgj > m.
; и tgj > m.

Определим отношение выделившейся при ударе теплоты и кинетической энергии налетающего шарика. Разница кинетических энергий шарика до и после удара перешла в тепло. Q = Eк,н – Ек,к
 ;
;
 , но
, но
 .
.
Искомое отношение
 .
.
Задача №15
Двигатели самолета прекратили работу на некоторой высоте над землей, когда вектор скорости имел величину v0 и был направлен под углом α к горизонту.
Найти изменение импульса самолета за время дальнейшего движения, пока он не окажется на той же высоте. Сопротивлением воздуха пренебречь
Решение.
Движение самолета осуществляется под действием только силы тяжести, т.е. по параболе. Поэтому можно построить схему

Dt = t - время движения, т.е. время действия силы тяжести на самолет.
На сколько изменится импульс тела брошенного под углом к горизонту за время движения?
 . Из чертежа
. Из чертежа
 ;
;  .
.
Поэтому

Задача №16
Два груза массой m и m1 соединены нерастяжимой невесомой нитью, перекинутой через неподвижный блок. Определить давление на ось блока, ускорение груза, натяжение нити. Массой блока и трением пренебречь. Принять, что 
Решение.
Запишем второй закон Ньютона, выбрав направления осей х по направлению ускорений в каждой ветви системы (см. схему).
Для тела m1:

Для тела m2:


Для нити:  , но нить невесома
, но нить невесома  :
:
Поскольку нить нерастяжима, то

 ,
,  ,
,




 - сила действующая со стороны подвеса
- сила действующая со стороны подвеса
Выясним, когда силы, действующие на блок, больше, при движении грузов или когда они неподвижны.


 т.к.
т.к.  . Ответ запишем в виде
. Ответ запишем в виде

Задача №17
Гимнаст висит на канате, перекинутом через блок. К другому концу каната привязан противовес массой m1. Система неподвижна. Затем гимнаст стал скользить по канату вниз, в момент времени t скорость противовеса больше скорости гимнаста относительно земли на u. Найти силу трения, возникшую при спуске гимнаста. Весом каната пренебречь, масса гимнаста m2.
Решение.
При равновесии к гимнасту приложена сила трения равная силе натяжения каната, т.е. Т = FТР. Если гимнаст движется по канату с ускорением а1, то груз перемещается с ускорением а2. Запишем 2-ой закон Ньютона:
Для противовеса
 ,
,
отсюда 
Для человека массой m2:  ;
;
отсюда 
Движение начиналось из состояния покоя, поэтому
 ;
; 



Задача №18
Вывести общее выражение для скорости, которую необходимо сообщить телу у поверхности Земли, чтобы оно вращалось по круговой орбите на высоте h от Земли и определить работу по выводу его на орбиту.
Решение
Искомая работа состоит из двух частей:
А1 – это работа, затраченная на сообщение спутнику скорости, необходимой для вращения на орбите.
А2 – работа необходимая для подъёма спутника на заданную высоту.
 сумма этих работ равна кинетической энергии на старте.
сумма этих работ равна кинетической энергии на старте.
 скорость спутника при старте
скорость спутника при старте
 кинетическая энергия, сообщённая спутнику при старте.
кинетическая энергия, сообщённая спутнику при старте.
 изменение потенциальной энергии спутника.
изменение потенциальной энергии спутника.
Определим эту величину:

 радиус Земли, М – масса Земли
радиус Земли, М – масса Земли
 (1)
(1)
Уравнение движения спутника по окружности радиуса R3 + h:
 .
.
Отсюда
 ;
;  . (2*)
. (2*)
Тогда
 (3)
(3)
Сила тяжести – это сила тяготения на поверхности земли.
 ; поэтому
; поэтому 
В (3) используем соотношение для приближенных вычислений
 ; Х << 1
; Х << 1
Тогда при h << R3





 - работа, необходимая для подъёма спутника на высоту h.
- работа, необходимая для подъёма спутника на высоту h.
Задача
Рассчитать момент инерции стержня и диска при вращении вокруг оси, указанной на рис.
Решение
Рассмотрим стержень, вращающийся вокруг оси проходящей через торец и перпендикулярной к оси симметрии стержня.

Выделим в стержне слой толщиной dx, находящийся на расстоянии х от оси вращения проходящей через торец стержня. этот слой имеет массу dm. Тогда момент инерции выделенного слоя 
Однако  , где r - плотность материала стержня, S - поперечное сечение стержня. Итак,
, где r - плотность материала стержня, S - поперечное сечение стержня. Итак,
 . Теперь просуммируем моменты инерции всех бесконечно тонких слоев, т.е. проинтегрируем
. Теперь просуммируем моменты инерции всех бесконечно тонких слоев, т.е. проинтегрируем

Полная масса стержня

Здесь V - объем стержня. Тогда

Рассмотрим диск. вращающийся вокруг оси, перпендикулярной его плоскости и проходящей через центр тяжести.

Поступаем также, как и в предыдущем случае, но суммировать будем моменты инерции бесконечно тонких колец, на которые разобьем диск.

Пусть h - толщина диска

 ;
; 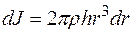
 ;
; 

Задача №19
Определить момент инерции шара относительно оси, проходящей через его центр.
Рис. 1 

Рис.2
Решение 1.
Выделим в шаре цилиндрический слой толщиной dr и высотой h. Тогда масса этой трубки (рис. 1)

Тогда момент инерции J0 этой массы dm, все точки, которой находятся на одинаковом расстоянии от оси вращения, запишется в виде:

 плотность материала.
плотность материала.
Из геометрии
 ,
,  .
.
Путём интегрирования можем получить момент инерции J всего шара.
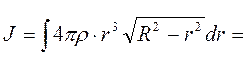 .
.
Интегрируя по частям, получаем
 но
но  поэтому
поэтому 
Решение 2.
Можно решить задачу, разделив шар плоскостями, перпендикулярными оси вращения на тонкие шаровые пояса (диски) (рис.2).





 ;
; 

(Интегрирование произведем заменой переменной R2 – r2 = U2)
Задача №20
Доска массой М плавает по воде. На одном конце, в точке А сидит лягушка. С какой минимальной скоростью она должна прыгнуть, чтобы попасть в точку В на этой же доске (АВ = L). Масса лягушки m. Трением доски о воду пренебречь.
Решение
Скорость будет минимальна, если угол между начальной скоростью и горизонтом в системе координат связанной с доской составляет 450:

 , поскольку импульс сохраняется в горизонтальном направлении.
, поскольку импульс сохраняется в горизонтальном направлении.


 ;
; 
Задача №21
Система состоит из двух материальных точек, массами m1 и m2, которые движутся с взаимно перпендикулярными скоростями u1 и u2 соответственно. В течение некоторого времени на систему действовала сила, которая изменила скорость 1-й частицы на противоположную. Найти величину и направление скорости 2-й частицы после действия силы.
Решение
V1 m1 m2 m1 V1к

Δp1 m2
V2
P2H P2K
Импульс силы, изменивший скорость первой частицы V1, действует также на вторую частицу и меняет ее скорость V2.
Найдём изменение импульса первой частицы:




-такой же импульс подействовал и на вторую частицу.


Эти векторы образуют прямоугольный треугольник
Из этого треугольника:


Задача №22
Диск массой М закреплён на неподвижной оси и вращается в горизонтальной плоскости с угловой скоростью w0. На край диска прыгает человек массой m. Как изменилось вращение диска? Радиус диска R, человека считать материальной точкой.
Решение
Состояние вращения может изменить только момент внешней силы.
 ,
, 


Значит, если в данном направлении появится момент силы  , то за время его действия появится изменение момента импульса
, то за время его действия появится изменение момента импульса  , изменение вектора момента импульса на
, изменение вектора момента импульса на  приведет к изменению угловой скорости
приведет к изменению угловой скорости  . В результате этого ось отклонится в направлении, перпендикулярном плоскости (R, mg), однако она фиксирована жёстко, т.е. в подшипнике возникает усилие с таким моментом силы, который компенсирует момент
. В результате этого ось отклонится в направлении, перпендикулярном плоскости (R, mg), однако она фиксирована жёстко, т.е. в подшипнике возникает усилие с таким моментом силы, который компенсирует момент  . Но все эти силы внутренние. Состояние вращения не изменится. Момент сил относительно оси w остался равным нулю. Хотя момент сил постоянный, но поменялось распределение масс, т.е. изменится момент инерции относительно прежней оси вращения, значит
. Но все эти силы внутренние. Состояние вращения не изменится. Момент сил относительно оси w остался равным нулю. Хотя момент сил постоянный, но поменялось распределение масс, т.е. изменится момент инерции относительно прежней оси вращения, значит
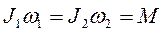

Поскольку момент инерции - функция аддитивная, то к моменту инерции диска в новой ситуации нужно прибавить момент инерции человека относительно этой же оси.
 ;
; 





