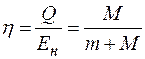Пусть заданы координаты точек m1, m2 и m3. Совместим начало координат с точкой m1. Тогда по общим формулам
; 
; 
;
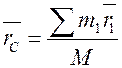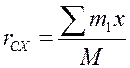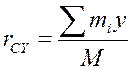xc = (m2x + m3x)/(m1 + m2 + m3); yc = (m3y)/(m1 + m2 + m3)
Второй способ:
Находим центр масс точек m1 и m2, лежащих на оси х.
m1xA = m2(l3 – xA),
где l3 = x2; l22 = x23 + y23; l221 = (x2 - x3)2 + (y2 – y3)2.
Находим угол Ðm3m2 = a.. По теореме косинусов
l21 = l22 + l23 + 2l2l3cosa,
отсюда, cosa = -(l22 + l23 – l21)/ 2l2l3.
Находим отрезок m3xA = d:
d2 = l22 + x2A – 2l2xAcosa
Находим положение точки С (центра масс) на отрезке d. отсчитываем искомый отрезок S = m3C из точки m3
m3S = (m1 + m2)(d – S).
Отсюда S = ((m1 + m2)/m1 + m2 + m3))d.
Положение центра масс сплошного треугольника (листа металла в форме треугольника постоянной толщины и плотности) определяется точкой пересечения меридиан треугольника.
Центр масс стержневого треугольника (стержня одинаковой толщины из материала постоянной плотности) находится на пересечении срединных перпендикуляров
Задача №38
Однородная пластина имеет форму буквы «Г» (см. рис.). Определить положение центра тяжести.
Решение
Разобьем пластинку на две части в виде прямоугольников, координаты центра тяжести, которых в выбранной системе координат легко найти (см. рис.).
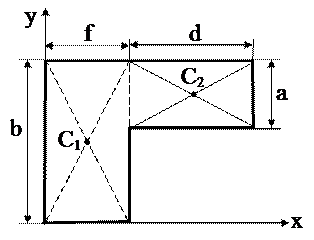
Имеем
Хс2 = f + d/2; Yc1 = b/2; Xc1 = f/2; Yc2 = a/2
По определению:
; 
; 
.
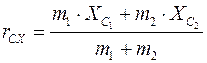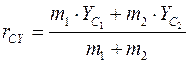Массу однородной пластинки выразим через плотность материала ρ, площадь S и толщину h:
m = ρSh; m1 = ρS1h; m2 = ρS2 h; S1 = bf; S2 = ad.
Окончательно имеем:
rcx = ((bf2/2) + ad (f + d/2))/(bf + ad);
rcy = ((b f/2) + a d /2))/(bf + ad).
Задача №39
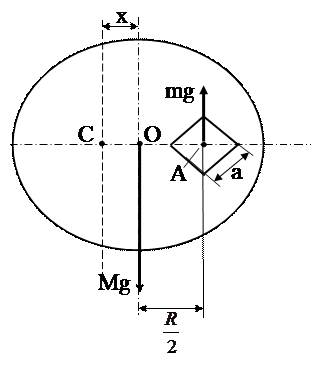
Имеется однородный круглый брелок, постоянной толщины, причем на его радиусе R посередине сделано квадратное отверстие cо стороной a, одна из диагоналей которого направлена по радиусу. Найти положение центра масс (ц.м.).
Решение
Для того чтобы получить отверстие,
необходимо на сплошной диск наложить
«отрицательную массу» m, равную по
величине массе вещества в отверстии.
Сила тяжести, действующая на такую массу,
направлена вверх. Тогда:
; 
;
; 
.
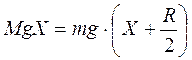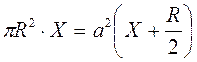Задача №40
Лестница массой m приставлена к стене. На ее середине находится человек массой М. АВ = l2 , BC = l1. Под каким углом установится лестница. Коэффициенты трения о стену и о пол соответственно равны m1 и m2.
Решение
Уравнение равновесия в проекциях по ОХ:
1) 
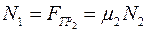
2) по ОУ:
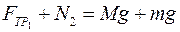
Сумма моментов сил относительно точки А –
; 
; 
; 
; 
;
.
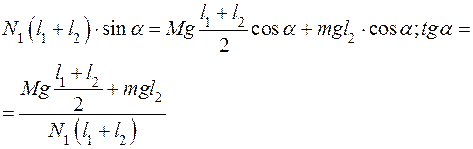
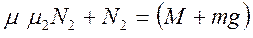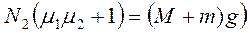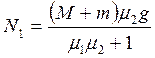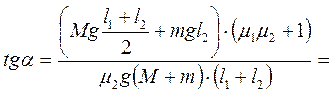
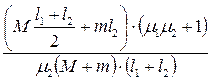Задача №41
Система состоит из двух тел. Известны зависимости от времени импульсов этих тел.
` p1= (2t + 3)`i + 3t2`j + 7`k; `p2 = - 2t`i + t`j.
Сохраняется ли импульс системы? Сохраняется ли какая-либо проекция этого импульса на декартовы оси координат? Чему равна результирующая внешняя сила, приложенная к системе?
Решение
Сложим импульсы тел, составляющих систему:
` P = `Р1+ `Р2 = 3`i+ (3t2 + t)`j +7`k
Так как суммарный импульс изменяется со временем, то он не сохраняется и на систему действует внешняя сила.
Проекции суммарного импульса на оси Х и Z не зависят от времени, поэтому в плоскости ХZ импульс системы сохраняется.
Поскольку внешняя сила равна производной импульса по времени, то
.
Задача №42
На гладкой поверхности обыкновенного стола лежит тонкий однородный стержень массой m и длиной L. На конец стержня перпендикулярно его оси действует импульс силы F, направленный горизонтально. А) на какое расстояние передвинется центр масс стержня за время полного своего оборота? Б) чему равны энергии поступательного и вращательного движений стержня и его полная кинетическая энергия после воздействия импульса силы?
Решение.
А) пусть v0 – скорость центра масс стержня, а θ0 – угловая скорость вращения стержня относительно центра масс.
В случае импульсного воздействия справедливы следующие уравнения движения:
F = mV0, FL/2 = Iθ′0, или θ′0 = FL/2I,
где I = (1/3)m(L/2)2 – момент инерции стержня относительно оси, проходящей через центр масс.
Если за время t стержень совершает полный оборот, то
θ′0t = FL/2I, откуда t = 2π/θ′0.
Следовательно, за время полного оборота центр стержня переместится на расстояние
S = V0t = F/m · 2π /θ′0.
Подставляя сюда выражение θ′0 = FL/2I, находим
S = F/m · πmL2/ 3FL = πL/3.
Энергия поступательного движения
Tп = m/2·V2o = ½ m·F2/m2 = ½F2/m.
Энергия вращательного движения
Tв =½Iθ′2o = ½ I (LF/2I)2 = 3/2 F2/m.
Полная кинетическая энергия стержня равна их сумме:
Tполн = Tп + Tв = 2F2/m.
Задача №43
Упругий шарик падает по вертикали с высоты h на горизонтальную плиту, отскакивает от нее вверх, вновь падает на плиту и т.д., продолжая это движение. Найти путь, пройденный шариком до остановки, если коэффициент восстановления при ударе равен K (см рис). Согласно Ньютону, отношение модуля нормальной составляющей относительной скорости точки контакта тел после удара к его значению до удара есть некоторая физическая постоянная не зависящая от массы тел и их относительной скорости. Она называется коэффициентом восстановления при ударе K.
Решение.
Пусть n – номер удара, тогда
K = V2/ V1 = h2/h11/2 = h3/h21/2 = … = hn+1/hn.
h2 = k2h1; h3 = k2h2 = k4h1; h4 = k2h3 = k6h1; h5 = k2h4 = k8h1;
hn+1 = k2nh1;
h = h1 +2h2 + 2h3+ 2h4 +… = h1 + 2h1(k2 + k4 + k6+…) =
= h1(1+2(k2/(1 - k2))) = h(1+k2/(1- k2)).
Задача №44
Опыт показывает, что если тело, закрепленное на оси вращения, подвергается удару, то действие удара в общем случае передается и на ось. При этом, величина и направление силы, приложенной к оси, зависят от того, в какую точку тела нанесен удар. При каких условиях отдача, действующая на ось, будет минимальна, т.е. найти положение центра удара.
Решение.
Рассмотрим сплошной однородный стержень АВ, подвешенный в точке А на горизонтальной, закрепленной в подшипниках оси OO' (рис. 1). Если удар (короткодействующая сила F (нанесен близко к оси вращения, то ось прогибается в направлении действия силы F (рис. 1а). Если удар нанесен по нижнему концу стержня, вблизи точки В, то ось прогибается в противоположном направлении (рис. 1б). Наконец, если удар нанесен в строго определенную точку стержня, называемую центром удара (рис. 1в, точка С), то ось не испытывает никаких дополнительных нагрузок, связанных с ударом. Очевидно, в этом случае скорость поступательного движения, приобретаемого точной А вместе с центром масс O, будет компенсироваться линейной скоростью вращательного движения вокруг центра масс О (оба эти движения инициируются силой F и происходят одновременно).
|
| Рис. 1. |
Вычислим, на каком расстоянии l от точки подвеса стержня находится центр удара. Уравнение моментов относительно оси вращения OO' дает
 
| (1) |
Сил реакции со стороны оси, как предполагается, при ударе не возникает, поэтому на основании теоремы о движении центра массможно записать
| (2) |
где m- масса тела, v0 - скорость центра масс. Если a - расстояние от оси до центра масс тела, то
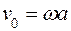
| (3) |
и в результате из уравнения моментов и уравнения движения центра масс находим
| (4) |
При этом точка C (центр удара) совпадает с так называемым центром качания данного физического маятника - точкой, где надо сосредоточить всю массу твердого тела, чтобы полученный математический маятник имел такой же период колебаний, как и данный физический.
В случае сплошного однородного стержня длиной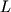 
имеем:
|
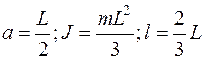
Замечание. Полученное выражение для l (4) справедливо и для произвольного твердого тела. При этом надо только иметь в виду, что точка подвеса тела А и центр масс О должны лежать на одной вертикали, а ось вращения должна совпадать с одной из главных осей инерции тела, проходящих через точку А.
Пример 1. При ударах палкой длиной L по препятствию рука "не чувствует" удара (не испытывает отдачи) в том случае, если удар приходится в точку, расположенную на расстоянии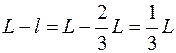 
от свободного конца палки.
Пример 2. При горизонтальном ударе кием по бильярдному шару (рис. 2) шар начинает качение без проскальзывания в том случае, еcли удар нанесен в точку, находящуюся на высоте
|
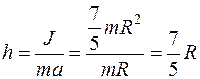
от поверхности бильярда, то есть на
выше центра шара. Если удар будет нанесен ниже, качение будет сопровождаться скольжением в направлении движении шара. Если удар нанесен выше, то шар в точке касания с бильярдным столом будет проскальзывать назад.
|
| Рис. 2. |
Рассмотренные примеры формально не относятся к вращению твердого тела вокруг неподвижной оси, однако все приведенные выше соображения о центре удара, очевидно, остаются в силе и в этих случаях.
Задача № 45
По небольшому куску мягкого железа, лежащего на наковальне массой М = 300 кг, ударяет молот массой m = 8 кг. Определить к.п.д. η удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
Решение.
Закон сохранения импульса: mu0 = (m + M) u, здесь m – масса молота, u0 – его скорость; М – масса наковальни, u - скорость отскока молота с наковальней (в результате взаимодействия с третьими телами). 
- запас энергии молота. Закон сохранения энергии:
;
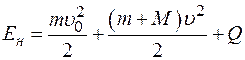Q – энергия, идущая на нагрев молота и наковальни и их деформацию. Нагревом пренебрегаем, как и деформацией молота. Тогда
к.п.д. 
