Если давление в пласте выше давления насыщения, то весь газ полностью растворен в жидкости и она ведет себя как однородная. При снижении давления ниже давления насыщения из нефти выделяются пузырьки газа. По мере приближения к забою скважины давление падает и размеры пузырьков увеличиваются вследствие расширения газа и одновременно происходит выделение из нефти новых пузырьков газа. Здесь мы имеем дело с фильтрацией газированной жидкости, которая представляет собой двухфазную систему (смесь жидкости и выделившегося из нефти свободного газа).
При фильтрации газированной жидкости рассматривают отдельно движение каждой из фаз, считая, что жидкая фаза движется в изменяющейся среде, состоящей из частиц породы и газовых пузырьков, а газовая фаза — в изменяющейся среде, состоящей из породы и жидкости. Полагая, что фильтрация происходит по линейному закону, записывают его отдельно для каждой фазы, вводя коэффициенты фазовых проницаемостей k* и kr, которые меняются в пласте от точки к точке:
(5.110)
здесь Q1 - дебит свободного газа в пластовых условиях.
Опытами Викова и Ботсета установлено, что фазовые проницаемости зависят главным образом от насыщенности перового пространства жидкой фазой σ. Насыщенностью σ называется отношение объема пор, занятого жилкой фазой, ко всему объему пор в данном элементе пористой среды. В результате опытов построены графики зависимостей относительных фазовых проницаемостей
k'ж= kж / k и k'r = kr/k от насыщенности σ для несцементированных песков (рис.5,27), для песчаников (рис.5.28), известняков и доломитов (рис.5.29); здесь k - абсолютная проницаемость породы, определяемая из данных по фильтрации однородной жидкости.
В теории фильтрации газированной жидкости вводится понятие газового фактора Г, равного отношению приведенного к атмосферному давлению дебита свободного и растворенного в жидкости газа к дебиту жидкости:
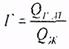(5.111)
При установившейся фильтрации газированной жидкости газовый фактор остается постоянным вдоль линии тока.
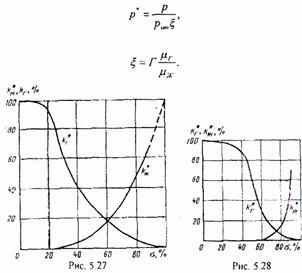
Так как насыщенность является однозначной функцией давления, то относительную фазовую проницаемость жидкой фазы kж можно связать с давлением и построить график kж (р') (рис.5.30), где безразмерное давление
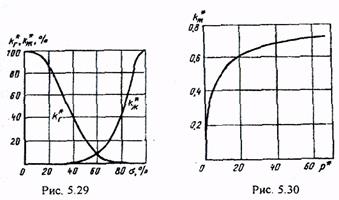
Назовем функцией С. А. Христиановича выражение
(5.112)
Через функцию Христиановича дебит жидкой фазы записывается по закону Дарси, в котором роль давления играет функция Н:
(5.113)
При определении дебита жидкой фазы и распределения давления при установившемся движении газированной жидкости справедливы все формулы, выведенные для однородной несжимаемой жидкости с заменой давления на функцию Христиановича. Например, дебит жидкой фазы газированной жидкости скважины, находящейся в центре горизонтального кругового пласта, определяется согласно формуле Дюпюи:
(5.114)
а дебит жидкой фазы галереи шириной В в пласте длиной l равен
(5.115)
Функция Христиановича в условиях плоскорадиальной фильтрации газированной жидкости подчиняется логарифмическому закону распределения 
(5.116)
а при параллельно-струйной фильтрации - линейному закону
(5.117)
При расчетах по методу Б.Б. Лапука значения функции Христиановича находят следующим образом. Путем графического интегрирования строят безразмерную функцию Христиановича
используя график k'ж(p*). Зависимость Н* от р* представлена на рис.5.31 для трех значений α=Sμ1 /μжрат(1-α=0,020; 2 - α=0,015; 3 -α=0,010). Определяют
величину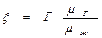 
, затем переходят от размерного давления к безразмерному при помощи формулы
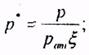(5.118)
по рис.5.31 находят значение Н*, соответствующее подсчитанному значению р*. Переходят к размерной функции Христиановича:
(5.119)
Для нахождения давления в некоторой точке пласта сначала определяют
значение функции Н по формуле (5.116) или (5.117), затем, используя график зависимости Н*(р*) (см.рис.5.31), переходят к соответствующему значению давления.
Отметим, что функция Христиановича зависит, кроме давления (величины переменной в пласте), от постоянного параметра α=Sμ1 /μжрат, где S - объемный коэффициент растворимости газа в жидкости.
И. А. Чарным было отмечено, что зависимость Н*(р*), согласно графику (см. рис.5.31), в широком диапазоне значений р* изображается почти прямой линией (при рс/рк>0,2), поэтому приближенно можно принять, что
(5.120)
и, следовательно,
(5.121)
где А 
0,944 - 21,43 а.
Г. Б. Пыхачев отмечает, что даже если давление в пласте меняется в широких пределах, фазовая проницаемость k'ж изменяется слабо, поэтому приближенно можно считать ее постоянной и равной значению фазовой проницаемости, соответствующей средневзвешенному давлению в пласте (k'ж). При этом
(5.122)
Задача 36
В пласте имеет место фильтрация газированной нефти. Определить, при каких насыщенностях жидкостью и газом фазовая проницаемость для жидкости kж равна фазовой проницаемости для газа kг. Найти величину этой
фазовой проницаемости, если абсолютная проницаемость мористой среды
k=0,8мкм2. Рассмотреть случаи, когда коллектор представлен несцементированным песком, песчаником, известняками и доломитами.
Указание. Воспользоваться графиками зависимостей фазовых проницаемостей от насыщенности жидкостью порового пространства (см. рис. 5.27, 5.28, 5.29).
Задача 37
Через пористую среду, представленную несцементированным песком, фильтруется газированная жидкость. Абсолютная проницаемость пористой среды k=5 мкм2, вязкость жидкости μж=1мПа*с, вязкость газа μг=0,012 мПа*с, насыщенность жидкостью порового пространства σ =65%.
Определить фазовые проницаемости kжи kг; сравнить сумму фазовых проницаем остей с абсолютной проницаемостью пористой среды, найти отношения скоростей фильтрации жидкости и газа ωж/ωги скоростей движения v ж lv г.
Задача 38
В полосообразном пласте происходит установившаяся параллельно-струйная фильтрация газированной жидкости по закону Дарси. Ширина пласта В=600 м, длина пласта L=3 км, толщина h=10 м, абсолютная проницаемость пласта k=0,15 мкм2, коэффициенты вязкости нефти и газа в пластовых условиях соответственно равны μж= 1,12 мПа*с, μг=0,014 мПа*с, коэффициент растворимости газа в нефти S=l,22*10-s мэ/м3*Па, газовый фактор Г=350 м3/м3. Давление на контуре питания рк=14,7 МПа, на забое галереи поддерживается давление рг=10,8 МПа.
Определить дебит галереи и давление в точке, расположенной на расстоянии х=2,5 км от контура питания.
Указание. Воспользоваться графиком зависимости функции Н* от безразмерного давления р* (рис.5.3.).
Задача 39
В центре нефтяного пласта радиуса Кк=350 м находится эксплуатационная скважина радиуса rс=0,1 м.
В каждой точке пласта давление ниже давления насыщения, поэтому имеет место движение газированной нефти. Определить дебиты нефти и газа, распределение давления в пласте и построить индикаторную диаграмму, если давление на забое скважины рс=8,82 МПа, давление на контуре питания рк=13,2 МПа, абсолютная проницаемость пласта k=0,1 мкм2, толщина пласта h=10 м, коэффициенты вязкости нефти μн= 1,2 мПа*с и газа μ г-0,012 мПа*с, коэффициент растворимости газа в нефти S=1,53*10-5 м3/м3*Па, газовый фактор Г = 400 м3/м3, paт= 1,01*105 Па.
Зависимость Н* от р* для α=0,015 приведена ниже.
| р* | |||||||||||
| Н* | 0,1 | 0,3 | 0,6 | 0,95 | 1,32 | 1,72 | 2,15 | 2,15 | 3,08 | 3,56 | |
| р* | |||||||||||
| Н* | 4,56 | 5,65 | 7,85 | 10,18 | 11,36 | 12,56 | 13,76 | 16,2 | 17,50 |
Решение. Дебит нефти при установившейся плоскорадиальной фильтрации газированной жидкости определим по формуле
для чего найдем значения функции Христиановича Нк и Нс при давлениях рк и рс. Подсчитаем коэффициент α=Sμ1 /μжрат, который является параметром при определении функции Христиановича Н:
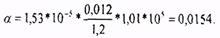
Определим значение безразмерного газового фактора
и безразмерные давления на контуре питания и на забое скважины:
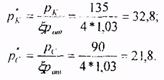
По таблице зависимости между безразмерными значениями давления р* и функции Христиановича Н при α =0,015 найдем Нк* =16,75 и Нс=10,06 и перейдем к размерным значениям
При этом дебит нефти
дебит газа
Распределение функции Христиановича в пласте определяется по формуле
Распределение давление получим, задаваясь различными значениями r, определяя значения Н и Н* при заданных Rk, rc, Hk,Hcи по значениям Н* - значения р* и р. Результаты расчетов приведены в табл.5.2
Таблица 5.2
| r, м | Н, МПа | Н* | Р* | р, МПа (кгс/см2) |
| 0,1 | 4,06 | 10,06 | 21,80 | 8,82(90) |
| 1,0 | 4,83 | 12,00 | 25,07 | 10,1(103} |
| 10,0 | 5,60 | 13,85 | 28,00 | 11,3(115) |
| 100,0 | 6,35 | 15,70 | 31,12 | 12,5Q28)_ |
| 350,0 | 6,77 | 16,75 | 32,80 | 13,2(135) |
Для построения индикаторной диаграммы задаемся различными значениями рс и для этих значений по формуле
подсчитаем дебиты qh(табл.5.3, рис.5.32).
Таблица 5.3
| Рс, МПа (кгс/см2) | рс* | Нс* | QH, м3 /сут |
| 12,25(125) | 30,4 | 15,25 | 34,3 |
| 10,78(110) | 26,7 | 12,98 | 86,4 |
| 8,82(90) | 21,8 | 10,06 | 154,0 |
| 4,95(50) | 12,1 | 4,61 | 276,0 |
| 0,98(10) | 2,43 | 0,43 | 372,0 |
| 0,101(1,03) | 0,25 | 0,025 | 382,0 |
Задача 40
В пласте имеет место установившаяся плоскорадиальная фильтрация газированной нефти по закону Дарси.
Выяснить, в каком случае при заданной депрессии Δр=2,45 МПа и заданном газовом факторе Г=200м3/м3 будет более высокий дебит нефти, если пластовые давления различны: 1) рк =9,8 МПа; 2) рк=4,9 МПа. Коэффициенты вязкости нефти μж=1 мПа*с и газа μж=0,012 мПа*с, коэффициент растворимости газа в нефти
S=1,73*IO-5м3/м3*Па.
Указание. Воспользоваться графиком зависимости Н* от р* (рис.5.31).
Задача 41
Сравнить дебиты при установившейся плоскорадиальной фильтрации газированной нефти по закону Дарси при разных газовых факторах и одной и
той же депрессии. Отношение 
= 100, коэффициент растворимости газа в той же нефти S=1,02*10-5 м3/м3*Па, рат=9,8*-104 Па, давление на контуре питания рк=11,76 МПа, давление на забое скважины рс=9,8 МПа. Газовые факторы Г1=300 м3/м3 и Г2=б00 м3/м3. Пласт представлен несцементированным песком.
