Скважина называется гидродинамически совершенной, если она вскрывает пласт на всю толщину и забой скважины открытый, т. е. вся вскрытая поверхность забоя является фильтрующей поверхностью. Поток жидкости к совершенной скважине — плоский фильтрационный поток. Если скважина с открытым забоем вскрывает пласт не на всю толщину, а только на некоторую величину Ь, или если скважина сообщается с пластом через отдельные отверстия, то фильтрация жидкости или газа будет пространственной (трехмерной), а скважина — гидродинамически несовершенной.
Различают три вида несовершенства скважин:
1) скважина гидродинамически несовершенная по степени вскрытия пласта — это скважина с открытым забоем, вскрывшая пласт не на всю мощность;
2) скважина гидродинамически несовершенная по характеру вскрытия пласта — скважина, вскрывающая пласт от кровли до подошвы, но сообщающаяся с пластом через отверстия в колонне труб, в цементном кольце или в специальном фильтре;
3) скважина гидродинамически несовершенная как по степени вскрытия пласта, так и по характеру вскрытия.
Дебит скважины, несовершенной по степени вскрытия, можно определить по
формуле М. Маскета, если радиус пласта 
(5.61)
(5.62)
и относительное вскрытие пласта ћ =b/h.
Функция φ(ћ) имеет следующее аналитическое выражение:
(5.63)
где Г - интеграл Эйлера второго рода или иначе, гамма-функция, для которой имеются таблицы в математических справочниках; φ(ћ представлена графически на рис.5.16.
Для скважины в пласте бесконечной толщины (рис.5.17) можно найти дебит при помощи формулы Н. К. Гиринского:
(5.64)
Дебит скважины гидродинамически несовершенной как по степени, так и по характеру вскрытия пласта можно подсчитать по формуле
(5.65)
где С1- безразмерная величина, определяющая дополнительное фильтрационное сопротивление, обусловленное несовершенством скважины по степени вскрытия пласта; С2- безразмерная величина, определяющая дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по характеру вскрытия пласта.
С1 и С2находятся из графиков В. И. Щурова, построенных по данным исследования притока жидкости к скважинам с двойным видом несовершенства на электролитических моделях.
Величина С1представлена на рис.5.18 в зависимости от параметров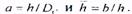 
.
На рис.5.19, 5.20, 5.21 дана зависимость С2 от трех параметров:
где n - число перфорационных отверстий на 1 м; Dc - диаметр, скважины в м; Г - глубина проникновения пуль в породу; d0 - диаметр отверстий.
Соответствие между кривыми и значениями параметра α=d0/ D видно из следующих данных:
Формулу (5.65) можно записать иначе, введя в нее приведенный радиус скважины
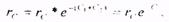
т.е. радиус такой совершенной скважины, которой равен дебиту
несовершенной скважины.
В литературе приводятся графики δ, которые можно использовать для
оценки С.
(5.67)
Иногда гидродинамическое несовершенство скважин учитывается при помощи коэффициента совершенства скважины
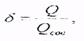(5.68)
где Q - дебит несовершенной скважины; Qcов- дебит совершенной скважины в тех же условиях.
Коэффициент совершенства скважины δ и величина С=С1+С2связаны между собой зависимоcтью
(5.69)
или
(5.70)
Задача 24
Используя график В. И. Щурова, найти коэффициенты С1и С2, определяющие дополнительные фильтрационные сопротивления, обусловленные несовершенством скважины, соответственно по степени и по характеру вскрытия, а также приведенный радиус скважины rcсчитая, что нефть притекает к скважине диаметром dc =24,7см, несовершенной как по степени, так и по характеру вскрытия. Толщинапласта h=12 м, вскрытие пласта b=7 м.,число прострелов на 1 м вскрытой толщины пласта n=17 отв./м, глубина проникновения пуль в породу l’=6,25 см, диаметр отверстия d0=l,l см.
Задача 25
Определить коэффициент совершенства скважины, несовершенной по характеру вскрытия. Забой скважины обсажен и перфорирован при помощи кумулятивного перфоратора, число круглых отверстий на 1м n=10, диаметр отверстия d0=16 мм, длина канала l’=100 мм, радиус скважины rc=10 см, расстояние до контура питания RK=500 м.
Задача 26
Определить коэффициент С1,учитывающий дополнительное фильтрационное сопротивление, приведенный радиус rc, и коэффициент совершенства δ гидродинамически несовершенной по степени вскрытия скважины радиусом rc=0,1м, находящейся в пласте с круговым контуром питания. Толщина пласта h=16 м, толщина вскрытой части пласта b= 9,6 м, радиус контура питания rk=1 км.
