Проницаемость в различных точках продуктивных пластов не является строго постоянной величиной. Иногда изменение проницаемости по пласту носит столь хаотичный характер, что пласт можно рассматривать в среднем однородно проницаемым.
Если изменение проницаемости носит не случайный характер, а на значительном протяжении пласта имеют место определенные закономерности в изменении проницаемости, тогда движение жидкостей и газов существенно отличается от движения их в однородных пластах.
Отметим следующие простейшие случаи неоднородности пластов.
1. Пласт состоит из нескольких слоев (рис.5,22, 5.23). В пределах каждого слоя проницаемость в среднем одинакова и скачкообразно изменяется при переходе от одного слоя к другому. Допустим, что все п слоев горизонтальны, толщина i-го слоя hi, проницаемость соответствующего слоя ki. На одном конце каждого слоя давление равно рк, на другом – рг.
Если движение жидкости прямолинейно-параллельное (см. рис.5.22) по закону Дарси, то распределение давления р в каждом слое линейное и характеризуется уравнением
(5.71)
дебит потока вычисляется по формуле
(5.72)
а средний коэффициент проницаемости по формуле
(5.73)
В случае плоско радиального движения жидкости в многослойном пласте к гидродинамически совершенной скважине по закону Дарси (см. рис.5.23) давление в каждом слое меняется по логарифмическому закону
(5.74)
дебит скважины определяется по формуле
(5.75)
а средний коэффициент проницаемости пласта и в этом случае находится по (5.73).
2. Пласт состоит из нескольких зон различной проницаемости {рис.5. 24, 5.25). На границе двух зон проницаемость меняется скачкообразно; в пределах одной и той же зоны проницаемость в среднем одинакова. С неоднородностью такого рода можно встретиться, например, при соприкосновении двух разных пластов вдоль сброса или п случае наличия порога фациалыюй изменчивости одного и того же пласта.
Допустим, что горизонтальный пласт толщиной h, длиной l с непроницаемыми кровлей и подошвой состоит из n зон различной проницаемости. Длина i-й зоны li, коэффициент проницаемости ki(см. рис.5.24).
При прямолинейно-параллельной фильтрации жидкости в таком пласте по закону Дарси дебит фильтрационного потока подсчитывается по формуле
(5.76)
где В - ширина потока.
Средний коэффициент проницаемости
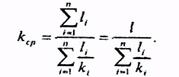(5.77)
При n=2 распределение давления в первой зоне р1, и во второй - р2 описывается уравнениями:
(5.78)
Если при плоскорадиальном притоке жидкости к гидродинамически совершенной скважине по закону Дарси зоны различной проницаемости пласта имеют кольцеобразную форму (см. рис.5.25), то формула дебита скважины имеет вид
(5.79)
где ki- коэффициент проницаемости зоны за номером i; ri-1 и ri -соответственно внутренний и внешний радиусы этой зоны, причем r0 = гс, а rп=Rk.
Средний коэффициент проницаемости в этом случае находится по формуле
(5.80)
При n=2 распределение давления в первой зоне р1, и во второй зоне р2 определяется по формулам:
(5.81)
3. Проницаемость пласта непрерывно изменяется, увеличиваясь или уменьшаясь в каком-либо направлении. Допустим, что при плоскорадиальном течении коэффициент проницаемости изменяется по линейному закону
У забоя скважины коэффициент проницаемости равен kc, а на контуре питания (r=RK) k = k0.
Фильтрация жидкости происходит по закону Дарси. В этом случае формула для дебита имеет вид
(5.82)
Задача 27
Определить средневзвешенный по толщине коэффициент проницаемости пласта, представленного несколькими проницаемыми пропластками, разделенными глинистыми пропластками. Жидкость движется в направлении напластования. Толщина и коэффициент проницаемости каждого пропластка указаны ниже.
Задача 28
Определить средневзвешенный по длине коэффициент проницаемости неоднородного пласта, состоящего из двух пластов, соединенных последовательно (см. рис.5.24). Первый пласт имеет длину l1=8 км и k1=0,5 мкм2, второй пласт — длину l1=1км и k2=1мкм2, рк=9,8 МПа, рг=4,9 МПа. Построить график распределения давления в пласте.
Задача 29
Определить средний коэффициент проницаемости пласта в зоне радиуса RK=500 м, если первоначальный коэффициент проницаемости всего пласта k2=1,2 мкм2, а затем в результате запарафинирования коэффициент проницаемости призабойной зоны радиусом r1=30 м снизился до k1=0,I5 мкм2. Радиус скважины rс=0,1 м.
Задача 30
Скважина радиусом rс=10 см эксплуатирует пласт радиусом RK =10 км с коэффициентом проницаемости k2. Во сколько раз изменится дебит скважины, если:
а) проницаемость в призабойной зоне радиуса r=0,5 м возрастет в 10 раз в результате ее обработки (k1: k2=10)?
б) проницаемость этой же призабойной зоны ухудшится в 10 раз
(k1: k2=0,1)?
в) рассмотреть ту же задачу при r=5 м. Сравнить полученные результаты.
Задача 31
Какие давления должны быть на забое скважины радиуса rс=10 см, чтобы получать один и тот же дебит для случаев: 1) когда пласт радиуса RK=10 км по простиранию однородный с коэффициентом проницаемости k2=l мкм2 2) когда пласт делится на две зоны с k2=0,15 мкм2 в призабойной зоне радиуса r1=5м и
k2=1 мкм2 в остальной части пласта? Пластовое давление рк=147 МПа депрессия в однородном пласте рк -рс=2,94 МПа.
Решение. По условию задачи дебит однородного пласта
равен дебиту неоднородного пласта
откуда
т. е. давление на забое скважины должно быть снижено почти в 2 раза для поддержания того же дебита.
