Фильтрационный поток называется радиально-сферическим, если векторы скорости фильтрации направлены в пространстве по прямым, радиально сходящимся к одной точке (или расходящимся от нее).
Благодаря центральной симметрии давление и скорость фильтрации
зависят и в этом случае только от одной координаты r, отсчитываемой от центра (рис.5.3). Примером потока, весьма близкого к радиально-сферическому, является приток жидкости к гидродинамически несовершенной скважине малого диаметра, едва вскрывшей непроницаемую горизонтальную кровлю однородного пласта большой мощности (теоретически бесконечной).
Если на забое скважины, представленной в виде полусферы радиуса rc., поддерживается постоянное приведенное давление рc, а на достаточно большом расстоянии от скважины, на полусферической поверхности радиуса Rk. сохраняется постоянное давление рk и фильтрация в однородном пласте происходит по закону Дарси, то объемный дебит скважины определяется по формуле
(5.29)
Приведенное давление в любой точке пласта определяется по формуле
(5.30)
а закон движения частиц вдоль линии тока отточки с координатой г0 до точки с
координатой r описывается уравнением
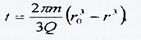(5.31)
Задача 4
Определить дебит дренажной галереи шириной В =100 м, если толщина пласта h=10 м, расстояние до контура питания l=10 км, коэффициент проницаемости пласта k=l мкм2, динамический коэффициент вязкости жидкости μ=1 мПа*с, давление на контуре питания рk=9,8 МПа и давление в галерее рk = 7,35 МПа. Движение жидкости напорное, подчиняется закону Дарси.
Задача 5
Определить коэффициент проницаемости пласта, если известно, что в пласте происходит одномерное, прямолинейно-параллельное установившееся движение однородной жидкости по закону Дарси. Гидравлический уклон i=-0,03, ширина галереи В=300 м, толщина пласта h=6 м, плотность жидкости ρ=850 кг/м1, динамический коэффициент вязкости μ=5 мПа*с и дебит галереи Q=30 м3/сут
Задача 6
Показать графически распределение давления и найти градиент давления при прямолинейно-параллельном движении в пласте несжимаемой жидкости по линейному закону фильтрации, используя следующие данные: длина пласта 1«=5 км, толщина пласта h=10 м, ширина галереи В=300 м, коэффициент проницаемости пласта k=0,8 мкм2, давление в галерее рг=2,94 МПа, динамический коэффициент вязкости жидкости μ =4 мПа*с, дебит галереи Q=30 м3/сут.
Задача 7
Определить дебит нефтяной скважины (в т/сут) в случае установившейся плоскорадиальной фильтрации жидкости по закону Дарси, если известно, что давление на контуре питания рк=9,8 МПа, давление на забое скважины рс = 7,35 МПа, коэффициент проницаемости пласта k=0,5 мкм2, толщина пласта h=15 м, диаметр скважины Dc=24,8 см, радиус контура питания RK=10 км, динамический коэффициент вязкости жидкости ^=6 мПа*с и плотность жидкости ρ = 850 кг/м3.
Задача 8
Определить давление на расстоянии 10 и 100 м от оси скважины при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, считая, что коэффициент проницаемости пласта k=0,5 мкм", толщина пласта h=10 м, давление на забое скважины
рс=7,84 МПа, радиус скважины rс=12,4 см, динамический коэффициент вязкости нефти μ=4 мПа*с, плотность нефти ρ=870 кг/м3 и массовый дебит скважины Q m=200 т/сут.
Задача 9
Построить индикаторную линию (зависимость дебита Q от перепада давления, имеющуюся при установившейся плоскорадиальной фильтрации жидкости по линейному закону, если известно, что давление на контуре питания рк=8,82 МПа, коэффициент проницаемости пласта k=0,6 мкм, толщина пласта h=10 м, диаметр скважины Dc=24,8 см, расстояние от оси скважины до контура питания RK=10 км и динамический коэффициент вязкости нефти μ=5 мПа*с.
Задача 10
Определить коэффициент гидропроводности пласта kh/p по данным о коэффициенте продуктивности скважины. Известно, что фильтрация происходит по закону Дарси, коэффициент продуктивности К=1,8 т/сут (МПа), среднее расстояние между скважинами 2о--1400 м, плотность р=925 кг/м3, радиус скважины гс=0,1 м.
Задача 11
Определить средневзвешенное по объему пластовое давление, если известно, что давление на контуре питания рк=9,8 МПа, давление на забое возмущающей скважины рс=7,84 МПа, расстояние до контура питания Rk=25 км, радиус скважины rc=10 см. В пласте имеет место установившееся плоскорадиальное движение несжимаемой жидкости по закону Дарси.
Задача 12
Определить время отбора нефти из призабойной зоны скважины радиусом г0=100 м, если толщина пласта h=10 м, коэффициент пористости пласта m=20%, массовый дебит нефти Qm=40 т/сут, плотность ее ρ=920 кг/м3, гс=0,1 м.
Задача 13
Определить время t, за которое частица жидкости подойдет к стенке скважины с расстояния r0=200 м, если коэффициент проницаемости пласта k=1мкм", динамический коэффициент вязкости нефти μ =5 мПа*с, депрессия во всем пласте радиусом Rk=1км составляет рk-рс=1 МПа; толщина пласта h=10м, коэффициент пористости пласта m=15%, радиус скважины гс =10 см.
Задача 14
Как изменится дебит скважины Q при увеличении радиуса скважины вдвое?
1. Движение происходит по линейному закону фильтрации.
2, Фильтрация происходит по закону Краснопольского. Начальный радиус скважины rс=0,1 м. Расстояние до контура питания RK=5 км.
