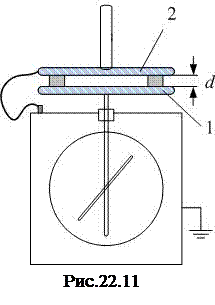
 Пластина 1 вместе с корпусом 5 образуют конденсатор ёмкостью С УСТ., так как изолированы друг от друга. Ёмкость установки С УСТ. Можно определить с помощью плоского конденсатора ёмкостью С ПЛ., который получится, если на пластину 1 установки положить пластину 2 с изолирующими ножками высотой d (рис.22.11). Поскольку пластина 2 заземлена, то конденсаторы С УСТ. и С ПЛ. окажутся соединены параллельно (докажите это!), и общая ёмкость равна сумме ёмкостей:
Пластина 1 вместе с корпусом 5 образуют конденсатор ёмкостью С УСТ., так как изолированы друг от друга. Ёмкость установки С УСТ. Можно определить с помощью плоского конденсатора ёмкостью С ПЛ., который получится, если на пластину 1 установки положить пластину 2 с изолирующими ножками высотой d (рис.22.11). Поскольку пластина 2 заземлена, то конденсаторы С УСТ. и С ПЛ. окажутся соединены параллельно (докажите это!), и общая ёмкость равна сумме ёмкостей:
 .
.
Полный заряд системы установка – плоский конденсатор сохранится, тогда
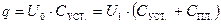 , (22.12)
, (22.12)
где U 0 – напряжение на установке без дополнительной пластины 2, U 1 – напряжение на установке после того, как на пластину 1 положили пластину 2. Из (22.12) получим расчётную формулу:
 . (22.13)
. (22.13)
Методика определения ёмкости проводника (шара)
В комплект установки входят два металлических шара, ёмкости которых можно определить с помощью установки. Методика измерений такая же, как и при определении ёмкости установки: при соединении незаряженного шара и пластины 1 установки заряд её, сохраняясь, только перераспределяется между установкой и шаром.
 . (22.14)
. (22.14)
Здесь С ШАР – ёмкость шара. Однако возникают две сложности.
 1) Длина проводника должна быть такова, что на соответствующем расстоянии заряженные установка и шар не влияли друг на друга, то есть чтобы их взаимная ёмкость была бы ещё достаточно мала. В качестве такого проводника используется пластина 3 с металлическим стержнем 9 (рис.22.8 и 22.12). Длина стержня такова, что при меньшем расстоянии между шаром и установкой уже нельзя было бы пренебрегать взаимной ёмкостью шара и установки.
1) Длина проводника должна быть такова, что на соответствующем расстоянии заряженные установка и шар не влияли друг на друга, то есть чтобы их взаимная ёмкость была бы ещё достаточно мала. В качестве такого проводника используется пластина 3 с металлическим стержнем 9 (рис.22.8 и 22.12). Длина стержня такова, что при меньшем расстоянии между шаром и установкой уже нельзя было бы пренебрегать взаимной ёмкостью шара и установки.
Таким образом, перед измерением ёмкости шара нужно на пластину 1 положить пластину 3 (рис.22.12). Однако при этом изменяется (увеличивается) ёмкость установки, и требуется снова её определить. При добавлении незаряженной пластины полный заряд сохраняется, поэтому
 , откуда
, откуда
 , (22.15)
, (22.15)
где где U 0 – напряжение на установке без дополнительной пластины 3, U 1 – напряжение на установке после того, как на пластину 1 положили разряженную пластину 3.
2) Ёмкость шара мала по сравнению с ёмкостью установки, поэтому разница в показаниях прибора до и после касания разряженным шаром заряженной установки невелика при однократном касании. Можно проделать процедуру несколько раз, каждый раз перед касанием шаром установки разряжая шар, тогда их (22.14) получим:  после первого касания;
после первого касания;  после второго касания, что даст:
после второго касания, что даст:
 ,
,
 после третьего касания; и тогда
после третьего касания; и тогда
 ,
,
и так далее. Окончательно получим после N касаний:
 ,
,
или
 . (22.16)
. (22.16)
Порядок выполнения работы
Задание 1. Определение ёмкости установки
Для определения ёмкости установки необходимо:
1. Измерить диаметр D пластин установки.
2. Измерить высоту d ножек на пластине 2.
3. Рассчитать ёмкость С ПЛ. плоского конденсатора по формуле (22.3):
 . (22.3)
. (22.3)
Все величины занести в табл. 22.1.
4. Снять пластину 2 с пластины 1 установки и поместить её на заземлённые опоры 3.
5. Зарядить установку. Для этого:
а) Потереть линейку бумагой (или тряпочкой из целлюлозного волокна);
б) положить линейку на пластину 1 установки;
в) прикоснуться рукой к пластине, снимая с неё индуцированный заряд;
г) убрать линейку.
Стрелка электрометра при этом должна отклониться примерно на 60÷70 делений.
6. Занести в таблицу 22.1 угол отклонения стрелки электрометра α0. Используя градуировочную таблицу 22.4, определить соответствующее углу α0 напряжение U 0.
7. Положить на пластину установки заземлённую пластину 2.
8. Записать новое значение угла отклонения электрометра α1 и определить напряжение U 1.
9. Убрать пластину 2, снова подзарядить установку (пункт 5) и повторить пункты 6-8. Повторить измерения α0 и соответствующих им α1 3 раза.
10. По формуле (22.13)
 (22.13)
(22.13)
вычислить ёмкость установки С УСТ., рассчитать среднее значение.
Таблица 22.1.
| № | D, м | d, м | С ПЛ, пФ | α0, дел. | U 0, В | α1, дел. | U 1, В | С УСТ, пФ | |
| Среднее: | |||||||||
Задание 2. Определение ёмкости установки с пластиной 3
Для определения ёмкости С УСТ.2 нужно:
1. Зарядить установку, как описано в пункте 5 предыдущего задания.
2. Записать угол отклонения стрелки прибора α0 в таблицу 22.2.
3. Разрядить пластину 3, прикоснувшись ею о зачищенные «рёбра» 10 (рис.22.8) заземлённого корпуса установки. При этом держать пластину 3 за изолированную часть стержня.
4. Положить пластину 3 на пластину 1 установки (рис.22.12). Записать угол α1 отклонения стрелки прибора.
Таблица 22.2.
| № | α0, дел. | U 0, В | α1, дел. | U 1, В | С УСТ.2, пФ | |
| Среднее: | ||||||
5. Убрать пластину 3, снова подзарядить установку и повторить пункты 2-4. Повторить измерения α0 и соответствующих им α1 3 раза.
6. По градуировочной таблице 22.4 определить соответствующие углам α напряжения U.
7. По формуле (22.15) рассчитать ёмкость установки С УСТ.2 в каждом опыте, рассчитать среднее значение С УСТ.2.
 . (22.15)
. (22.15)
8. Все данные занести в таблицу 22.2.
Задание 3. Определении ёмкости шара
Для определения ёмкости шара необходимо:
1. Положить на пластину 1 установки пластину 3 с закреплённым на ней металлическим стержнем (рис.22.12).
2. Зарядить установку вместе с пластиной 3, как описано в п. 5 задания 1. Записать в табл.22.3 угол α0.
3. Взять большой шар за диэлектрическую ручку.
4. Снять с шара заряд, прикоснувшись им к зачищенным «рёбрам» 10 (рис.22.8) заземлённого корпуса установки.
5. Прикоснуться шаром к концу 9 металлического стержня пластины 3.
6. Повторить пункты 4 и 5 N раз (N =8÷16). Внимательно считать число касаний! Записать N и угол αN.
7. По градуировочной таблице определить напряжения U 0 и U N, соответствующие углам α0 и αN.
8. По формуле (22.16) вычислить экспериментальное значение ёмкости шара:
 . (22.16)
. (22.16)
9. Повторить эксперимент ещё 2 раза (пункты 2-8).
10. Найти среднее значение С ШАР.
11. Измерить радиус шара R. Рассчитать теоретическое значение С ШАР.Т. по формуле (22.17) и сравнить с экспериментальным.
 . (22.17)
. (22.17)
12. Результаты измерений и вычислений занести в табл.22.3.
Таблица 22.3. Большой шар
| № п/п | α0, дел. | U 0, В | N | αN,дел. | U N, В | С ШАР, пФ | R, м | С ШАР.ТЕОР., пФ |
| Среднее: |
13. Повторить измерения и вычисления по пунктам 2÷12 для меньшего шара.
14. Все результаты занести в табл.22.4.
Таблица 22.4. Малый шар
| № п/п | α0, дел. | U 0, В | N | αN,дел. | U N, В | С ШАР, пФ | R, м | С ШАР.ТЕОР., пФ |
| Среднее: |
Задание 3. Определение ёмкости цилиндрического конденсатора и диэлектрической проницаемости изоляции коаксиального кабеля
Для выполнения задания нужно:
1. Положить на пластину 1 установки заземлённую пластину 2.
2. Зарядить установку вместе с пластиной 2, как описано в п. 5 задания 1, положив заряженную линейку между обкладками получившегося плоского конденсатора на пластину 1.
3. Записать в табл.22.5 угол α0.
4. Разрядить цилиндрический конденсатор, роль которого играет кусок коаксиального кабеля 13 (рис.22.13). Для этого обоими оголёнными проводами 12 кабеля одновременно прикоснуться к заземлённому электроду 11 (22.13,а), не касаясь пластины 1.
 5. Прикоснуться оголёнными проводами кабеля одновременно к заземлённому электроду 11 и нижней пластине 1 плоского конденсатора (рис.22.13,б).
5. Прикоснуться оголёнными проводами кабеля одновременно к заземлённому электроду 11 и нижней пластине 1 плоского конденсатора (рис.22.13,б).
6. Записать в табл.22.5 угол α1.
7. Определить напряжения U 0 и U 1, соответствующие углам α0 и α1.
8. Повторить опыт ещё 2 раза (пункты 3÷7). Если нужно, подзаряжать установку (см. пункт 5 задания 1).
9. Рассчитать в каждом опыте экспериментальное значение ёмкости цилиндрического конденсатора по формуле (22.18):
 . (22.18)
. (22.18)
10. Рассчитать среднее значение С ЦИЛ..
11. Измерить длину l коаксиального кабеля.
12. Используя (22.6), рассчитать диэлектрическую проницаемость ε изоляции кабеля.
 , (22.6)
, (22.6)
где радиус внутренней жилки R 1=0.5 мм, радиус внешней оплётки R 2=2.5 мм.
12. Результаты всех измерений и вычислений занести в табл.22.5.
Таблица 22.5
| № | α0, дел. | U 0, В | α1, дел. | U 1, В | С ЦИЛ, пФ | R 1, мм | R 2, мм | l, м | ε |
| 0.5 | 2.5 | ||||||||
| Средние: |
13. Сделайте выводы.
Контрольные вопросы
1. Что называется емкостью проводника? Конденсатора?
2. Выведите формулу для емкости плоского конденсатора; сферического конденсатора; цилиндрического конденсатора.
3. Что такое электростатическая индукция?
4. Как можно зарядить электрометр?
5. Опишите методику определения ёмкости установки; проводника; цилиндрического конденсатора.
6. Выведите формулу для ёмкости изолированного шара.
Таблица 22.6.
Зависимость напряжения от угла отклонения стрелки электрометра
| α, дел. | U, В | α, дел. | U, В | α, дел. | U, В | α, дел. | U, В | α, дел. | U, В | α, дел. | U, В |
| 3.5 | |||||||||||
| 4.5 | |||||||||||
| 5.5 | |||||||||||
| 6.5 | |||||||||||
| 7.5 | |||||||||||
| 8.5 | |||||||||||
| 9.5 | |||||||||||
| 10.5 | |||||||||||
| 11.5 | |||||||||||
Используемая литература
[1] §§ 16.1-16.3;
[2] §§ 11.5, 11.6;
[3] §§ 2.15-2.18, 2.20, 2.22;
[4] т.2, §§ 26, 27;
[5] § 94.
Библиографический список
1. Детлаф, А.А. Курс физики/ А.А. Детлаф, Б.М. Яворский.-М.: Высш.шк., 1989.-500 с.
2. Калашников, Н.П. Основы физики: учебник для вузов: в 2-х т. / Н.П. Калашников, М.А. Смондырев. – 2-е изд., перераб. – М.: Дрофа, 2003. Т.1. - 400 с. Т.2. – 432 с.
3. Лозовский, В.Н. Курс физики: учебник для вузов: в 2-х т./ Под ред. В.Н. Лозовского. – СПб.: Лань, 2000.-Т.1-676с.; Т.2.-592с.
4. Савельев, И.В., Курс общей физики: учеб. пособие: в 3-х т. / И.В. Савельев.- 5-е изд., стер. – СПб.: Лань, 2006.
5. Трофимова, Т.И. Курс физики / Т.И. Трофимова. – М.:Высш. школа, 1999. - 542 с.






