Определение удельного заряда электрона методом магнетрона

Цель работы – изу­че­ние дви­же­ния за­ря­жен­ных час­тиц в скрещен­ных электри­че­ском и маг­нит­ном по­лях; оз­на­ком­ле­ние с ра­бо­той электровакуумной лампы 6Ж32П (или ин­ди­ка­то­ра 6Е5С); измерение удельного заряда электрона методом магнетрона.

 

Теоретическое введение

Удельным зарядом называется отношение заряда частицы к ее массе (e/m). На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, которую иначе называют магнитной:

, (17.1)

где q – заряд частицы; – ее скорость; 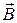– индукция магнитного поля.

Сила Лоренца перпендикулярна плоскости, в которой лежат векторы и 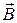. Модуль этой силы

, (17.2)

где a – угол между векторами и .

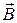Траектория движения заряженной частицы в магнитном поле определяется конфигурацией магнитного поля, ориентацией вектора скорости и отношением заряда частицы к ее массе.

Так как сила Лоренца пер­пен­ди­ку­ляр­на век­то­ру ско­ро­сти , то она может изменить не величину, а только направление скорости частицы.

Ес­ли в про­стран­ст­ве, где дви­жет­ся элек­трон, име­ют­ся од­но­вре­мен­но электриче­ское и маг­нит­ное по­ля, то сила, действующая на заряженную частицу, определяется по формуле Лоренца,

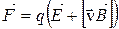, (17.3)

где – напряженность электрического поля. Первое слагаемое в формуле (17.3) представляет собой электрическую составляющую силы Лоренца, второе – магнитную:

. (17.4)

В об­щем слу­чае действия обеих составляющих бу­дет происходить из­ме­не­ние ско­ро­сти элек­тро­на как по ве­ли­чи­не, так и по направлению.

Существуют различные методы определения удельного заряда частиц e/m, в основе которых лежат результаты исследования движения электрона в электрическом и магнитном полях. Один из них – метод магнетрона. Называется он так потому, что конфигурация полей в нем напоминает конфигурацию полей в магнетронах – генераторах электромагнитных колебаний сверхвысоких частот.

Сущность метода состоит в следующем: специальная двухэлектродная электронная лампа, электроды которой представляют собой коаксиальные цилиндры, помещается внутри соленоида так, что ось лампы совпадает с осью соленоида. Пред­ста­вим се­бе на­хо­дя­щие­ся в ва­куу­ме металлический ци­линдр и ме­тал­ли­че­скую на­ка­ли­вае­мую нить, на­тя­ну­тую вдоль оси ци­лин­д­ра (рис.17.1).

 

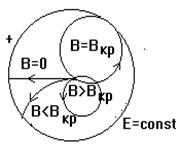Рис. 17.2

 

Если между ни­тью и ци­лин­дром при­ло­жить раз­ность потен­циа­лов так, что­бы нить явля­лась ка­то­дом, а ци­линдр – ано­дом, то электроны, вылетающие из ни­ти, бу­дут под дей­ст­ви­ем элек­три­че­ско­го по­ля притя­ги­вать­ся к ци­лин­д­ри­че­ско­му аноду. Их дви­же­ние бу­дет пря­мо­ли­ней­ным и ус­ко­рен­ным. Ес­ли до­пол­ни­тель­но соз­дать одно­род­ное маг­нит­ное по­ле внут­ри цилин­д­ра, век­тор индук­ции ко­то­ро­го параллелен оси ци­лин­д­ра, то вы­ле­таю­щие из ни­ти элек­тро­ны, пе­ре­се­кая линии маг­нит­ного по­ля, бу­дут дви­гать­ся уже не по ради­аль­ным, а по кри­вым ли­ни­ям. Ис­крив­ле­ние тра­ек­то­рии элек­тро­нов бу­дет тем боль­ше, чем боль­ше си­ла Лоренца, про­пор­цио­наль­ная ин­дук­ции магнит­но­го по­ля. Практически та­кое наложе­ние электри­че­ско­го и маг­нит­но­го полей мож­но осуществить, по­мес­тив элек­трон­ную лам­пу с цилиндри­че­ским анодом в со­ле­но­ид с то­ком. Ра­зо­грев катод и соз­дав не­ко­то­рую раз­ность потенциа­лов ме­ж­ду катодом и ано­дом, бу­дем пропускать че­рез со­ле­но­ид постоянный ток, соз­да­вая тем са­мым маг­нит­ное по­ле внут­ри ци­лин­д­ра-анода. Тогда на элек­трон, вылетевший из ка­то­да, одновременно бу­дут дей­ст­во­вать си­лы со сто­ро­ны электри­че­ско­го и маг­нит­но­го по­лей. Электриче­ская сила на­прав­ле­на по радиу­су от ка­то­да к ано­ду.

Z

Си­ла ис­крив­ля­ет траекторию дви­же­ния электро­на в плос­ко­сти, перпендику­ляр­ной к оси ка­то­да и ано­да (рис.17.2). Оче­вид­но, ес­ли В ма­ло, то траекто­рии элек­тро­нов бу­дут сла­бо искривле­ны и все элек­тро­ны бу­дут по­па­дать на анод. С уве­ли­че­ни­ем то­ка в соленоиде, со­от­вет­ст­вен­но и ин­дук­ции маг­нит­но­го по­ля, тра­ек­то­рии элек­тро­нов все боль­ше ис­крив­ля­ют­ся и при не­ко­тором критическом зна­че­нии ин­дук­ции траектории электронов только касаются анода (рис.17.3), а при элек­тро­ны больше не дос­ти­га­ют анода. Таким образом, при определенном соотношении между скоростью электрона и индукцией магнитного поля электроны перестают поступать на анод, и ток в лампе прекращается.

Рассмотрим подробнее движение электронов в лампе при наличии магнитного поля. Для описания этого движения воспользуемся цилиндрической системой координат (рис. 17.4), в которой положение электрона определяется расстоянием его от оси лампы r, полярным углом j и смещением вдоль оси Z. Электрическое поле, имеющее только радиальную компоненту, действует на электрон с силой, направленной по радиусу от катода к аноду. Магнитная сила, действующая на электрон, не имеет составляющей, параллельной оси Z. Поэтому электрон, вылетающий из катода без начальной скорости (начальные скорости электронов, определяе­мые температурой катода, много меньше скоростей, приобретаемых ими при движении в электрическом поле лампы), движется в плоскости, перпендикулярной оси Z.

Z

Момент импульса L_z электрона относительно оси Z:

(17.5)

где – составляющая скорости, перпендикулярная радиусу r. Момент М сил, действующих на электрон относительно оси Z, определяется только составляющей магнитной силы, перпендикулярной r. Электрическая сила и составляющая магнитной силы, направленные вдоль радиуса r, момента относительно оси Z не создают. Таким образом:

, (17.6)

где – радиальная составляющая скорости электрона.

По уравнению моментов

(17.7)

Проецируя (17.7) на ось Z, с учетом (17.6) получаем:

или

(17.8)

Интегриря уравнение (17.8), получаем: .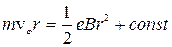

Константу найдем из начальных условий: при r = r _k (r _k – радиус катода) , тогда и

. (17.9)

Кинетическая энергия электрона равна работе сил электрического поля:

, (17.10)

где U – потенциал относительно катода точки поля, в которой находится электрон.

Подставляя в (17.10) значение 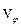из (17.9), получаем

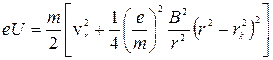(17.11)

При некотором значении индукции магнитного поля B _кр, которое называют критическим, скорость электрона вблизи анода станет перпендикулярной радиусу r. т.е. . Тогда уравнение (17.11) примет вид:

,

где U _а – потенциал анода относительно катода (анодное напряжение); r _a – радиус анода.

Отсюда находим выражение для удельного заряда электрона:

(17.12)

Таким образом, экспериментально определив В _кр, можно вычислить величину (e/m). Для нахождения В _кр в лампе следует установить разность потенциалов между анодом и катодом и, включив ток в соленоиде, постепенно наращивать его, что увеличивает магнитное поле в лампе. Если бы все электроны покидали катод со скоростью, равной нулю, то зависимость величины анодного тока от величины индукции магнитного поля имела бы вид, показанный на рис. 17.5 (пунктирная линия). В этом случае при B < B _кр все электроны, испускаемые катодом, достигали бы анода, а при B > B _кр ни один электрон не попадал бы на анод. Однако некоторая некоаксиальность катода и анода, наличие остаточного газа в лампе, падение напряжения вдоль катода, неоднородность поля соленоида по высоте анода и т.п. приводят к тому, что критические условия достигаются для разных электронов при различных значениях В. Все же перелом кривой остается достаточно резким и используется для определения В _кр.

Экспериментальная часть

Установка № 1 (новая)

Приборы и оборудование: модуль “Заряд электрона” (ФПЭ-03), источник питания (ИП), амперметр (РА). Функциональная схема лабораторной установки представлена на рис. 17.6.

 

 

Экспериментальная установка.

 

Основным элементом экспериментальной установки, содержащим соленоид и двухэлектродную лампу, является кассета ФПЭ–03 “Заряд электрона”, к которой подключается источник питания ИП и измерительный прибор Щ4313, как это показано на рис. 17.6. Катушка-соленоид закреплена между панелями, внутри соленоида соосно с ним установлена электровакуумная лампа 6Ж32П (рис.17.7).

Порядок выполнения работы

1. Подать напряжение на установку, включив источник ИП.

2. Установить анодное напряжение U _a=50 В по вольтметру ИП.

3. Изменяя ток в соленоиде от минимального (начального) значения до максимального через 0.1 А при постоянном анодном напряжении, снять сбросовую характеристику, то есть зависимость анодного тока I _a от тока в соленоиде I _cол. (рис. 17.8). Значения анодного тока I _a, определяемые по прибору РА, и значения тока в соленоиде I _cол., определяемые по показаниям амперметра ИП, занести в табл. 17.1.

 

 

Таблица 17.1

U a= 50 В	U a= 100 В	U a= 120 В
I cол., А	I a, мА	I cол., А	I a, мА	I cол., А	I a, мА

 

4. Повторить пункты 2 и 3 при двух других значениях анодного напряжения (100 В и 120 В). Результаты измерений занести в табл. 17.1.

5. Для каждого значения анодного напряжения построить сбросовую характеристику, откладывая по оси ординат значения анодного тока, а по оси абсцисс - значения тока в соленоиде. Для нахождения критического значения тока в соленоиде I _кр. провести до взаимного пересечения касательную к точке перегиба сбросовой характеристики (на участке до спада) и прямую, соответствующую изменению минимальных значений анодного тока (как показано на рис. 17.8). Занести полученные значения I _кр. в табл. 17.2.

6. Индукция магнитного поля соленоида, длина L которого соизмерима с диаметром D:

, (17.13)

где 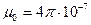Гн/м – магнитная постоянная; – число витков соленоида на единицу его длины. Для каждого критического значения тока в соленоиде рассчитать по формуле (17.13) индукцию магнитного поля. Длина соленоида L =167 мм; диаметр намотки D =85 мм; число витков соленоида N =2700.

7. Вычислить удельный заряд электрона e/m по формуле (17.12) для каждого значения критического поля в соленоиде и определить его среднее значение (e/m)_ср. Радиус анода r _a=1 мм; радиус катода r _к=0.1 мм.

8. Вычислить погрешность полученной величины (e/m).

9. Сравнить полученное в эксперименте значение удельного заряда электрона с табличным.

10. Сделать выводы.

Таблица 17.2

U a, В	I кр., А	B кр., Тл	(e/m), Кл/кг	(e/m)ср., Кл/кг	Δ(e/m), Кл/кг	(e/m)табл., Кл/кг

 

Установка № 2 (старая)

 

Приборы и оборудование: ис­точ­ник пи­та­ния, лам­па 6Е5С, соленоид, амперметр, двой­ной ключ, вольт­метр, рео­стат, пе­ре­мен­ное со­про­тив­ле­ние.

 

Рис. 17.9.

При определении удельного заряда электрона на данной установке критическое значение тока соленоида I _кроп­ре­де­ля­ет­ся пу­тем ви­зу­аль­но­го наблюде­ния све­че­ния ин­ди­ка­то­ра 6Е5С при из­ме­няю­щем­ся то­ке че­рез со­ле­но­ид. На рис. 17.9 по­ка­за­но с­хе­ма­ти­че­ское уст­рой­ст­во ин­ди­ка­то­ра 6Е5С, ко­торый со­сто­ит из ка­то­да 1 и эк­ра­на-ано­да 2. Эк­ран-анод вы­пол­нен в ви­де усе­чен­но­го сни­зу ко­ну­са. На внутреннюю по­верх­ность ко­ну­са на­не­се­но ве­ще­ст­во, ко­то­рое све­тит­ся под дей­ст­ви­ем элек­трон­ной бом­бар­ди­ров­ки зе­ле­ным све­том. Ко­гда ток в со­ле­нои­де от­сут­ст­ву­ет, элек­тро­ны дви­жут­ся от ка­то­да к ано­ду по пря­мым ли­ни­ям и све­тит­ся весь эк­ран рав­но­мер­но. С уве­ли­че­ни­ем то­ка в соленои­де уве­ли­чи­ва­ет­ся си­ла Ло­рен­ца, дей­ст­вую­щая на элек­тро­ны, и на эк­ра­не ин­ди­ка­то­ра на­блю­да­ет­ся ис­крив­ле­ние тра­ек­то­рии элек­тро­нов. При дос­ти­же­нии кри­ти­че­ско­го зна­че­ния то­ка в со­ле­нои­де I _кр элек­тро­ны на­чи­на­ют не до­ле­тать до эк­ра­на в его наи­бо­лее уда­лен­ной от ка­то­да час­ти, и эта об­ласть эк­ра­на пре­кра­ща­ет све­тить­ся. Об­ра­зу­ет­ся тем­ная (не­све­тя­щая­ся) ок­руж­ность ме­ж­ду кра­ем эк­ра­на и све­тя­щим­ся по­лем эк­ра­на.

Ин­дук­цию маг­нит­но­го по­ля внут­ри со­ле­нои­да для данной установки мож­но рас­счи­тать по фор­му­ле:

, (17.14)

так как , где I – сила тока в соленоиде, N – число витков соленоида; L – его длина, К – ко­эф­фи­ци­ент, учитывающий отличие поля в короткой ка­туш­ке от по­ля в длин­ной.

Для данной установки r _к<< r _а, поэтому величина в формуле (17.12). очень мала и ею можно пренебречь. Тогда формула (17.12) примет вид:

. (17.15)

Рис. 17.10

PA2 PA1     PV1

Для вы­пол­не­ния дан­ной ра­бо­ты при­ме­ня­ет­ся схе­ма, ука­зан­ная на рис.17.10 и со­стоя­щая из элек­трон­ной лам­пы 6E5С (1); со­ле­нои­да (L); источника пи­та­ния катода лам­пы напряже­ни­ем ~6.3 B; цепи питания анода напряжением U =350 B; пере­мен­но­го со­про­тивле­ния R₂; мил­ли­ам­пер­мет­ра PA1; вольт­мет­ра PV1; це­пи пи­та­ния со­ле­нои­да L, со­стоя­щей из вы­пря­ми­те­ля, = 24 В; пе­ре­мен­но­го со­про­тив­ле­ния R₁; клю­ча SA1; ампермет­ра PА2.

Рис. 17.11

Рас­по­ло­же­ние при­бо­ров на па­нель­ном щит­ке представлено на рис.17.11: 1 – циф­ро­вой при­бор Щ4313 для из­ме­ре­ния напряже­ния U _а; 2 – циф­ро­вой при­бор Щ4313 для из­ме­ре­ния си­лы то­ка I _кр. в це­пи ка­туш­ки; 3 – ка­туш­ка с ин­ди­ка­то­ром 6Е5С; 4 и 5 – рукоятки по­тен­цио­мет­ров для из­ме­не­ния напряжения; 6 – тумб­лер вклю­че­ния ус­та­нов­ки в сеть; 7 – ин­ди­ка­тор вклю­че­ния ус­та­нов­ки в сеть.

Перед началом работы:

– на приборе Щ4313 (1) долж­ны быть на­жа­ты кнопки: "пит", "V", "500", осталь­ные от­жа­ты;

– на приборе Щ4313 (2) долж­ны быть на­жа­ты кноп­ки: "пит", "А", "5", остальные от­жа­ты;

– на потенциометрах рукоятки 4 и 5 долж­ны быть в край­нем ле­вом положении (про­тив ча­со­вой стрел­ки до упо­ра).