Функциональная схема представлена на рисунке 18.5.

 |
В данной работе для исследования затухающих колебаний в реальном колебательном контуре, включающем активное сопротивление R, применяется электронный осциллограф. При этом через генератор звуковых колебаний производится периодическая подзарядка конденсатора, то есть кривая затухающих колебаний периодически повторяется.
 При не очень больших значениях сопротивления контура (
При не очень больших значениях сопротивления контура ( , где L – индуктивность катушки, С – емкость конденсатора)), на экране осциллографа наблюдается картина затухающих колебаний, как это показано на рис.18.6, что соответствует закону изменения напряжения
, где L – индуктивность катушки, С – емкость конденсатора)), на экране осциллографа наблюдается картина затухающих колебаний, как это показано на рис.18.6, что соответствует закону изменения напряжения
 .
.
Измерив амплитуды колебаний, отстоящие друг от друга на время, равное периоду:


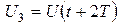 ,
,
можно определить логарифмический декремент затухания
 (18.22)
(18.22)
и его среднее значение
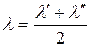 . (18.23)
. (18.23)
Или аналогично для тока:
 . (18.22а)
. (18.22а)
Тогда коэффициент затухания можно рассчитать как
 . (18.24)
. (18.24)
 Значение сопротивления в контуре можно изменять с помощью магазина сопротивлений (R маг.). Полное активное сопротивление контура R складывается из активного сопротивления катушки индуктивности R кат. и сопротивления магазина R маг.:
Значение сопротивления в контуре можно изменять с помощью магазина сопротивлений (R маг.). Полное активное сопротивление контура R складывается из активного сопротивления катушки индуктивности R кат. и сопротивления магазина R маг.:  . Из (18.17)
. Из (18.17) 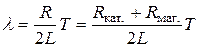 получим, что зависимость l = f (R маг.) логарифмического декремента затухания от сопротивления R маг. в контуре линейная (рис.18.7).
получим, что зависимость l = f (R маг.) логарифмического декремента затухания от сопротивления R маг. в контуре линейная (рис.18.7).
Значение R кат. можно определить, экстраполируя график до значения l®0. Индуктивность L катушки можно рассчитать по формуле (18.5) для коэффициента затухания:
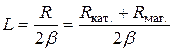 (18.25)
(18.25)
и, считая b << w 0, емкость С конденсатора из формулы Томсона (18.18):
 . (18.26)
. (18.26)

|
 При больших значениях сопротивления контура (
При больших значениях сопротивления контура ( ) на экране электронного осциллографа будет наблюдаться апериодический процесс, показанный на рис.18.8.
) на экране электронного осциллографа будет наблюдаться апериодический процесс, показанный на рис.18.8.
Измерения логарифмического декремента затухания l можно проводить также с помощью фазовой кривой U = f (I). Если сопротивление контура  , то фазовые кривые имеют вид, показанный на рис.18.4. При больших значениях сопротивления контура (
, то фазовые кривые имеют вид, показанный на рис.18.4. При больших значениях сопротивления контура ( ) фазовая кривая для апериодического разряда принимает вид, показанный на рис.18.9.
) фазовая кривая для апериодического разряда принимает вид, показанный на рис.18.9.
 В работе для получения колебаний в контуре используется модуль ФПЭ-10 с контуром, изображенным на рис.18.10. Если генератор задает частоту n ген., то цикл подзарядки конденсатора длится
В работе для получения колебаний в контуре используется модуль ФПЭ-10 с контуром, изображенным на рис.18.10. Если генератор задает частоту n ген., то цикл подзарядки конденсатора длится  секунд, этому времени на экране осциллографа соответствует отрезок d 1 (рис.18.6). Периоду колебаний T соответствует отрезок d. Следовательно, период затухающих колебаний может быть определен по формуле
секунд, этому времени на экране осциллографа соответствует отрезок d 1 (рис.18.6). Периоду колебаний T соответствует отрезок d. Следовательно, период затухающих колебаний может быть определен по формуле  , или:
, или:
 . (18.27)
. (18.27)
Сигнал в форме гармонического колебания заданной частоты с генератора PQ преобразователем ПИ преобразуется в последовательность прямоугольных импульсов той же частоты.
Будучи поданным на колебательный контур КК, импульс заряжает конденсатор С до напряжения U m, сообщая контуру начальный запас энергии. По окончании импульса происходит многократный разряд конденсатора С через индуктивность L и сопротивление R, то есть возникают затухающие колебания (рис.18.6).
Изменение коэффициента затухания β колебательного процесса осуществляется выбором величины резистора R маг. магазина сопротивления МС.
Порядок выполнения работы
Задание 1: Измерение периода, логарифмического декремента и параметров L, C, R колебательного контура.
1. На генераторе Г6-43 установить:
- режим работы: гармонические колебания;
- диапазон частот: 1К;
- аттенюатор: 0;
- амплитуду сигнала: ≈3 В;
- частоту (ручкой плавной регулировки): 150 Гц.
 2. На блоке преобразователя импульсов (ПИ) ФПЭ-08 нажать кнопку “ “ и правую клавишу “Скважность грубо”. Ручку “Скважность точно” установить в среднее положение.
2. На блоке преобразователя импульсов (ПИ) ФПЭ-08 нажать кнопку “ “ и правую клавишу “Скважность грубо”. Ручку “Скважность точно” установить в среднее положение.
3. На магазине сопротивлений установить сопротивление R маг.=100 Ом.
4. На осциллографе С1-150 установить:
- ручку развёртки «время/дел» в положение 1;
- ручку усилителя «вольт/дел» в положение 1 В;
- нажать кнопку  .
.
5. Подать напряжение на схему: включить источник питания ИП, генератор PQ, осциллограф PO.
6. Воздействуя на ручки развертки и усилителя осциллографа, получить на его экране полную кривую затухающих колебаний и зарисовать ее.
7. Измерить расстояния d, d 1 и вычислить период колебаний по (18.27).
8. Измерить амплитуды колебаний U 1, U 2, U 3 (рис.18.6) и по формулам (18.22), (18.23) вычислить логарифмический декремент затухания l. По формуле (18.24) определить коэффициент затухания b.
9. Результаты измерений занести в таблицу 18.1.
10. Выполнить измерения и расчеты по пунктам 7-9 для сопротивлений: 200, 300, 400, 500, 600, 700, 900 Ом.
11. По формуле (18.18) рассчитать добротность Q для R= 100, 300 и 500 Ом. Результаты записать в таблицу 18.2.
12. Построить график зависимости логарифмического декремента затухания l от сопротивления магазина R маг. (рис. 18.7). По графику определить R кат., экстраполируя график к l=0. Записать в таблицу 18.2.
13. Используя полученное значение R кат, вычислить индуктивность L в каждом опыте по формуле (18.25) и рассчитать среднее значение L ср..
14. Используя полученные в пункте 6 значения периода Т, рассчитать в каждом опыте емкость C по формуле (18.26); найти среднюю величину C ср.. Все полученные данные записать в таблицу 18.1.
Таблица 18.1
| R маг, Ом | ν, Гц | d, дел | d 1, дел | Т, с | U 1, дел | U 2, дел | U 3, дел | 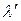
| 
| λ | b, с-1 | R = R кат.+ R маг., Ом | L, Гн | C, Ф |
| Средн. | - | - | - | - | - | - | - | - | - | - | - | - |
Таблица 18.2
| R кат., Ом | R маг.кр., опыт, Ом | R маг.кр., теор., Ом | Q | ||
| R= 100 Ом | R= 300 Ом | R= 500 Ом | |||
15. Опытным путем подобрать на магазине сопротивлений МС такое значение критического сопротивления R маг.кр., при котором в контуре будет наблюдаться апериодический процесс (рис. 18.8). Сравнить экспериментальное значение R маг.кр с величиной, полученной из условия  :
:
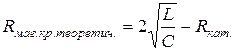 .
.
16. Все полученные данные записать в таблицу 18.2.
Задание 2. Исследование фазовых кривых.
Для наблюдения на экране фазовой кривой на вертикально отклоняющие пластины осциллографа подают напряжение с обкладок конденсатора, а на горизонтально отклоняющие пластины – напряжение U с клемм магазина сопротивлений R маг, пропорциональное току:  . Таким образом, на экране осциллографа изображается зависимость напряжения U на обкладках конденсатора от тока I в контуре.
. Таким образом, на экране осциллографа изображается зависимость напряжения U на обкладках конденсатора от тока I в контуре.
1. Установить на магазине сопротивлений МС сопротивление 100 Ом, на звуковом генераторе – частоту 100 Гц.
2. Включить осциллограф. Нажать кнопку «X-Y». Получить на экране фазовую кривую (рис. 18.4). Установить картину в центре экрана. Зарисовать фазовую кривую.
3. Непосредственно на фазовой кривой измерить значения напряжения и тока, отличающиеся по времени на период колебаний. Для этого определить расстояние от центра координат 0 фазовой плоскости до точек пересечения спирали с осями напряжения U и тока I (см. рис. 18.4). Вычислить логарифмические декременты затухания λ для напряжения и тока по (18.22), (18.22а). Измерения выполнить по всем виткам фазовой кривой. Результаты измерений занести в таблицу 18.3.
4. Повторить измерения по пунктам 3, 4 при значения сопротивления магазина R маг. 200, 300, 400, 500, 600, 700, 900 Ом.
5. Постепенно увеличивая R маг., получить апериодический процесс в колебательном контуре. Зарисовать апериодический процесс и его фазовую кривую.
Таблица 18.3
| R маг, Ом | U 1, дел | U 2, дел | U 3, дел | 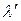
| 
| λ | I 1, дел | I 2 дел | I 3 дел | 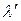
| 
| λ |
| По напряжению | По току | |||||||||||
Контрольные вопросы
1. Что такое колебательный контур?
2. Нарисуйте схему последовательного колебательного контура.
3. Объясните механизм возникновения электромагнитных колебаний в колебательном контуре.
4. Получите дифференциальное уравнение затухающий колебаний и запишите его решение.
5. Нарисуйте график затухающих колебаний. По какому закону уменьшается амплитуда затухающих колебаний?
6. Дайте определение коэффициента затухания, собственной частоты колебаний контура, декремента и логарифмического декремента затухания.
7. Дайте определение добротности. В чем заключается ее физический смысл?
8. При каких условиях в колебательном контуре возникает апериодический процесс?
9. Сформулируйте понятия фазовой плоскости и фазовой кривой.
10. Нарисуйте фазовые кривые для затухающего колебательного и апериодического процессов в колебательном контуре.
Используемая литература
[1] § 28.1;
[2] § 19.6;
[3] § 3.8;
[4] т.2, § 90;
[5] § 146.
Лабораторная работа 2-19
Изучение электрических процессов в простых линейных цепях при действии гармонической электродвижущей силы (ФПЭ-09)
Цель работы: изучение электрических процессов в цепях, состоящих из последовательно соединенных элементов: а) двух резисторов (цепь RR), б) резистора и конденсатора (цепь RC), в) резистора и катушки индуктивности (цепь RL):
а) измерение коэффициента передачи цепей RR, RC, RL; изучение зависимости коэффициента передачи цепей RC и RL от частоты входного сигнала;
б) оценка параметров цепей R, C, L;
в) определение разности фаз между колебаниями тока в изучаемых цепях и входным напряжением.
Теоретическое введение
Цепь переменного электрического тока представляет собой ряд соединенных между собой в той или иной последовательности элементов, в которых возбуждаются токи одним или несколькими источниками ЭДС.
Все элементы электрической цепи обладают сопротивлением. Это сопротивление может быть двух видов: активное или реактивное. Если при прохождении тока через элемент происходит только необратимое превращение электрической энергии в теплоту, то его сопротивление называют активным. Если же подобной потери электрической энергии не происходит, сопротивление элемента называют реактивным.
Элемент цепи с активным сопротивлением называется резистором. Реактивным сопротивлением – емкостным и индуктивным – обладают соответственно конденсаторы и катушки индуктивности.
Элементы цепи называются идеальными, если они обладают только одним видом сопротивления – активным, емкостным или индуктивным. Для идеальных элементов справедливы соотношения:
 ;
;  (19.1)
(19.1)
 ;
; 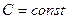 (19.2)
(19.2)
 ;
;  , (19.3)
, (19.3)
где  – сопротивление резистора;
– сопротивление резистора;  – емкость конденсатора;
– емкость конденсатора;  – индуктивность катушки;
– индуктивность катушки;  ,
,  ,
,  – падения напряжения (или просто напряжения) на соответствующих элементах;
– падения напряжения (или просто напряжения) на соответствующих элементах;  – ток через элемент;
– ток через элемент;  – заряд конденсатора;
– заряд конденсатора;  – ЭДС самоиндукции, возникающая в катушке индуктивности при прохождении через нее переменного тока.
– ЭДС самоиндукции, возникающая в катушке индуктивности при прохождении через нее переменного тока.
Элементы цепи могут быть линейными и нелинейными. Если сопротивление элемента не зависит от величины тока в цепи или от напряжения на элементе, то такой элемент называется линейным. Электрические цепи, составленные из линейных элементов, также называются линейными. В линейных цепях электрические процессы описываются линейными алгебраическими или дифференциальными уравнениями. Этому условию, например, отвечают выражения (19.1) – (19.3). Электрические процессы в линейных цепях называются установившимися (стационарными), если закон изменения всех токов и напряжений совпадает с точностью до постоянной величины с законом изменения внешней ЭДС, действующей в цепи. Если это условие не выполняется, процессы называются переходными.
При анализе электрических процессов в цепях переменного тока к мгновенным значениям тока можно применять законы Ома и Кирхгофа и другие правила, установленные для постоянного тока, если переменный ток является квазистационарным. Условие квазистационарности означает, что мгновенные значения переменного тока практически одинаковы на всех участках цепи. Это условие выполняется для медленно меняющегося тока, когда его мгновенное значение не успевает измениться за время распространения электрического процесса вдоль цепи. Если  – характерное время изменения мгновенного значения тока, а
– характерное время изменения мгновенного значения тока, а  – время распространения электрического процесса вдоль цепи протяженностью
– время распространения электрического процесса вдоль цепи протяженностью  со скоростью
со скоростью 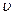 (равной по порядку величины скорости распространения электромагнитного возмущения
(равной по порядку величины скорости распространения электромагнитного возмущения  м/с), то условие квазистационарности запишется в виде:
м/с), то условие квазистационарности запишется в виде:  .
.
В дальнейшей будем полагать, что элементы цепи являются идеальными и, в соответствии с соотношениями (19.1) – (19.3), линейным. Электрические процессы будем считать установившимися, а переменные токи – квазистационарными.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора R, емкости C и индуктивности L (рис.19.1).
Допустим, что источник переменной ЭДС (генератор) не обладает внутренним сопротивлением  и создает на входе цепи напряжение U равное его ЭДС
и создает на входе цепи напряжение U равное его ЭДС 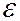 . Такое допущение всегда можно сделать, включив сопротивление генератора
. Такое допущение всегда можно сделать, включив сопротивление генератора  в состав рассматриваемой электрической цепи.
в состав рассматриваемой электрической цепи.
Положим далее, что ток в цепи
 (19. 4)
(19. 4)
создается в стационарном состоянии генератором с гармонической ЭДС
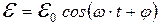 , (19. 5)
, (19. 5)
где  – круговая частота колебаний ЭДС и тока;
– круговая частота колебаний ЭДС и тока;  – период колебаний;
– период колебаний;  – угол сдвига фазы напряжения (ЭДС) относительно фазы тока;
– угол сдвига фазы напряжения (ЭДС) относительно фазы тока;  – амплитуда ЭДС;
– амплитуда ЭДС; 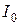 – амплитуда тока.
– амплитуда тока.
 |
Найдем, чему равны амплитуда тока 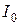 и сдвиг фаз
и сдвиг фаз  , если известны параметры цепи
, если известны параметры цепи  ,
,  ,
,  , и уравнение для ЭДС (19.5).
, и уравнение для ЭДС (19.5).
Одновременно определим, какой вид имеет величина 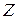 , равная отношению амплитуды ЭДС к амплитуде тока:
, равная отношению амплитуды ЭДС к амплитуде тока:  .
.
Эта величина (по аналогии с законом Ома для замкнутой цепи постоянного тока) называется полным сопротивлением цепи переменного тока. На основании второго правила Кирхгофа для контура на рис.19.1,а можем записать  или (рис. 19.1,б):
или (рис. 19.1,б):
 , (19.6)
, (19.6)
то есть сумма напряжений на отдельных элементах контура равна в каждый момент времени внешней ЭДС, действующей в контуре.
Учитывая соотношения (19.1) – (19.3), имеем
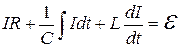 , (19.7)
, (19.7)
или, с учетом (19.5) и того, что  :
:
 . (19.7а)
. (19.7а)
Выражение (19.7а) представляет собой дифференциальное уравнение вынужденных колебаний. Подстановка в уравнение (19.7) выражений (19.4), (19.5) и выполнение операций интегрирования и дифференцирования приводит это уравнение к виду:

Используя далее соотношения
 ,
,  ,
,
окончательно получим:
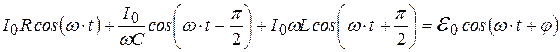 (19.8)
(19.8)
Из уравнения (19.8) можно сделать ряд выводов.
Выпишем из этого уравнения выражения для напряжений 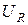 ,
,  ,
,  и рассмотрим их совместно с выражением (19.4) для тока
и рассмотрим их совместно с выражением (19.4) для тока  :
:
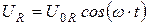 , где
, где  , (19.9а)
, (19.9а)
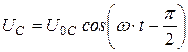 , где
, где  (19.9б)
(19.9б)
 , где
, где  . (19.9в)
. (19.9в)
Сравнивая фазы напряжений 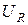 ,
,  и
и  с фазой тока
с фазой тока 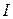 , видим, что:
, видим, что:
1) напряжение на резисторе 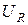 совпадает по фазе с током
совпадает по фазе с током 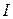 ;
;
2) напряжение на емкости  отстает по фазе от тока
отстает по фазе от тока 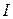 на угол
на угол  ;
;
3) напряжение на индуктивности  опережает по фазе ток
опережает по фазе ток 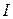 на угол
на угол  .
.
Далее найдем отношения амплитуд напряжений 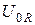 ,
, 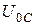 ,
,  к амплитуде тока
к амплитуде тока 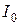 :
:
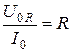 ;
;  ;
; 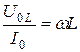 . (19.10)
. (19.10)
Формулы (19.10) определяют величины, которые называются соответственно активным, реактивным емкостным и реактивным индуктивным сопротивлениями. Емкостное сопротивление обозначается через  , индуктивное – через
, индуктивное – через  . Из формул (19.10) следует, что активное сопротивление цепи переменного тока равно сопротивлению цепи для постоянного тока, то есть омическому сопротивлению
. Из формул (19.10) следует, что активное сопротивление цепи переменного тока равно сопротивлению цепи для постоянного тока, то есть омическому сопротивлению  , реактивные же сопротивления:
, реактивные же сопротивления:
 ;
; 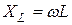 (19.11)
(19.11)
Перейдем к основной задаче: нахождению выражений, определяющих амплитуду тока 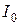 , сдвиг по фазе
, сдвиг по фазе  напряжения (ЭДС) и тока и полное сопротивление
напряжения (ЭДС) и тока и полное сопротивление 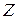 цепи, изображенной на рис. 19.1.
цепи, изображенной на рис. 19.1.
Уравнение (19.8) позволяет решить эту задачу, при этом методы решения могут быть различные. Воспользуемся графическим способом представления гармонических колебаний – методом векторных диаграмм. В этом методе гармоническим величинам (напряжениям, токам) сопоставляются вращающиеся векторы. Для этого на плоскости выбирают произвольное начало координат 0 и проводят ось X. Изучаемую гармоническую величину изображают вектором, построенным из начала координат. Длина вектора равна (в выбранном масштабе) амплитуде гармонической величины, а угол между вектором и осью X равен углу начальной фазы. Вектор равномерно вращается вокруг точки 0 с угловой скоростью  в направлении против часовой стрелки. При этом проекция вектора на ось Х в любой момент времени равна мгновенному значению гармонической величины, изменяющейся со временем по закону косинуса.
в направлении против часовой стрелки. При этом проекция вектора на ось Х в любой момент времени равна мгновенному значению гармонической величины, изменяющейся со временем по закону косинуса.
В соответствии со сказанным левую часть уравнения (19.8) можно рассматривать как сумму проекций векторов, изображающих напряжения 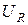 ,
,  и
и  , а правую часть – как проекцию вектора, изображающего суммарное напряжение
, а правую часть – как проекцию вектора, изображающего суммарное напряжение  . Поскольку при сложении векторов сумма проекций слагаемых равна проекции суммы, то можно найти геометрическую сумму векторов, изображающих напряжения
. Поскольку при сложении векторов сумма проекций слагаемых равна проекции суммы, то можно найти геометрическую сумму векторов, изображающих напряжения 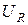 ,
,  ,
,  и приравнять эту геометрическую сумму вектору, изображающему напряжение
и приравнять эту геометрическую сумму вектору, изображающему напряжение  . Другими словами, вместо алгебраического равенства (19.8) можно рассматривать векторное равенство
. Другими словами, вместо алгебраического равенства (19.8) можно рассматривать векторное равенство
 , (19.12)
, (19.12)
причем модули векторов 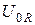 ,
, 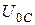 ,
,  определяются равенствами (19.9). Такое представление значительно упрощает нахождение амплитуды
определяются равенствами (19.9). Такое представление значительно упрощает нахождение амплитуды 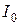 и сдвига фаз
и сдвига фаз  . На рис. 19.2 построены векторные диаграммы для момента времени t =0, соответствующие уравнениям (19.8) и (19.12).
. На рис. 19.2 построены векторные диаграммы для момента времени t =0, соответствующие уравнениям (19.8) и (19.12).
 |
Из рис. 19.2 следуют соотношения:
 и
и 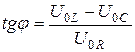 .
.
Поскольку вектора  и
и  направлены противоположно, и
направлены противоположно, и  , тогда, с учетом (19.12):
, тогда, с учетом (19.12):
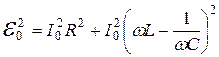 , (19.13)
, (19.13)
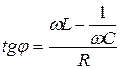 , (19.14)
, (19.14)
откуда
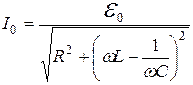 , (19.15)
, (19.15)
 , (19.16)
, (19.16)
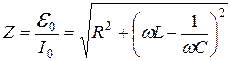 . (19.17)
. (19.17)
Видим, что колебания тока в цепи отстают по фазе от колебаний ЭДС на угол  , зависящий от частоты и определяемый уравнением (19.16). Можно также сказать, что напряжение
, зависящий от частоты и определяемый уравнением (19.16). Можно также сказать, что напряжение  во внешней цепи, содержащей последовательно соединенные
во внешней цепи, содержащей последовательно соединенные  ,
,  и
и  , опережает по фазе ток на угол
, опережает по фазе ток на угол  , определяемый выражением (19.16). Полное сопротивление цепи
, определяемый выражением (19.16). Полное сопротивление цепи 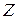 , в соответствии с (19.17), также зависит от частоты и может быть записано в виде:
, в соответствии с (19.17), также зависит от частоты и может быть записано в виде:
 , (19.18)
, (19.18)
где 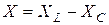 – полное реактивное сопротивление цепи. Из формулы (19.18) следует, что активное и реактивное сопротивления цепи складываются геометрически.
– полное реактивное сопротивление цепи. Из формулы (19.18) следует, что активное и реактивное сопротивления цепи складываются геометрически.
Методика измерений
В работе исследуются электрические процессы в цепях, состоящих из следующих последовательно соединенных элементов: а) двух резисторов с сопротивлениями R 1 и R 2 (цепь RR, рис. 19.3, а); б) резистора R 2 и конденсатора С (цепь RC, рис. 19.3, б); в) резистора R 2 и катушки индуктивности L (цепь RL, рис. 19.3, в).
Основным параметром, характеризующим изучаемые цепи, является коэффициент передачи цепи  , представляющий собой отношение амплитуды напряжения на выходе цепи
, представляющий собой отношение амплитуды напряжения на выходе цепи  к амплитуде напряжения на ее входе
к амплитуде напряжения на ее входе  :
:
 (19.19)
(19.19)
Напряжение на выходе цепи 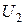 равно падению напряжения на резисторе
равно падению напряжения на резисторе  :
:
 , (19.20)
, (19.20)
то есть прямо пропорционально току в цепи 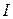 и находится в одинаковой с ним фазе. Или, для амплитудных значений:
и находится в одинаковой с ним фазе. Или, для амплитудных значений:
 . (19.20а)
. (19.20а)
   
U 2
| б) С U 1 R2 U 2 | в) U 1 R2 U 2 |
Рис.19.3
На основании соотношения (19.20а) коэффициент передачи цепи можно записать в виде:
 (19.21)
(19.21)
Из соотношения (19.20) следует, что для измерения угла сдвига фаз между током в цепи 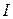 и входным напряжением
и входным напряжением  достаточно измерить угол сдвига фаз между напряжениями
достаточно измерить угол сдвига фаз между напряжениями 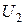 и
и  .
.
Для схем, изображенных на рис. 19.3, найдем аналитически вид выражений для коэффициента передачи цепи  и угла сдвига фаз
и угла сдвига фаз  . Для этого воспользуемся формулами (19.15), (19.16) и (19.21), подставляя в них соответствующие каждой схеме значения сопротивлений, напряжений и токов.
. Для этого воспользуемся формулами (19.15), (19.16) и (19.21), подставляя в них соответствующие каждой схеме значения сопротивлений, напряжений и токов.
1. Цепь RR:  ;
;  ;
;  ;
;  .
.
Из (19.15):
 ; (19.22)
; (19.22)
из (19.16):
 ; (19.23)
; (19.23)
из (19.21) и (19.22):
 . (19.24)
. (19.24)
2. Цепь RC:  ;
;  ;
;  ;
;  .
.
Из (19.15):
 ; (19.25)
; (19.25)
из (19.16):
 ; (19.26)
; (19.26)
из (19.21) и (19.25):
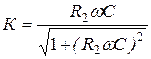 . (19.27)
. (19.27)
При высоких частотах (ω →∞):  ≈
≈  ; φ ≈0; К ≈1. Этот результат соответствует тому, что в цепи закорочен конденсатор С. При низких частотах (ω →0):
; φ ≈0; К ≈1. Этот результат соответствует тому, что в цепи закорочен конденсатор С. При низких частотах (ω →0):
 ;
; 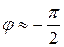 ;
;
 . (19.28)
. (19.28)
Этот результат соответствует тому, что в цепи закорочен резистор  .
.
3. Цепь RL: R = R2; ХL = ωL; ХС =0;  .
.
Из (19.15):
 ; (19.29)
; (19.29)
из (19.16):
 ; (19.30)
; (19.30)
из (19.21) и (19.29):
 . (19.31)
. (19.31)
При высоких частотах (ω →∞):
 ;
;  ;
;
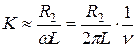 . (19.32)
. (19.32)
Это соответствует тому, что в цепи закорочен резистор R2. При низких частотах (ω→0):  ;
; 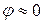 ;
;  . Это соответствует тому, что в цепи закорочена индуктивность L.
. Это соответствует тому, что в цепи закорочена индуктивность L.
Полученные результаты могут быть использованы для экспериментального определения параметров цепей R, С, L.
Экспериментальная часть
Приборы и оборудование: модуль ФПЭ-09, генератор (PQ), осциллограф (РО), источник питания (ИП).
На рис. 19.4 приведена электрическая схема.
В модуле ФПЭ-09 собраны изучаемые электрические цепи (рис.19.5). В нем находится также коммутатор А, применение которого позволяет наблюдать на экране однолучевого осциллографа одновременно два синусоидальных сигнала. Напряжение с входа изучаемой цепи подается на "Вx1" коммутатора, а напряжение с выхода изучаемой цепи – на "Вх2" коммутатора. С выхода коммутатора исследуемые напряжения подаются на вход Y осциллографа.

Рис. 19.4 Рис. 19.5
Генератор PQ является источником гармонической ЭДС. Выходное напряжение и частоту генератора можно менять в широких пределах.
Осциллограф РО служит для измерения амплитуд напряжений на входе и выходе цепи, а также для измерения угла сдвига фаз между током в цепи и входным напряжением.
Источник питания ИП предназначен для питания схемы коммутатора.
Порядок выполнения работы
Перед выполнением заданий ознакомиться с описаниями приборов, используемых в данной установке.
1. Установить исходное положение кнопочных переключателей на панели кассеты ФПЭ – 09: все кнопки отжаты.
2. Установить органы управления на панели осциллографа РО в положение, обеспечивающее измерение амплитуды и развертку во времени переменного напряжения. Ручку развёртки «Время/дел» поставить в положение «10», «Вольт/дел» – в положение «0.1». На панели осциллографа нажать кнопку «Внутр/внеш». Все остальные кнопки должны быть отжаты.
3. Присоединить все приборы к сети ~220 В. Включить приборы тумблерами «Сеть». Дать приборам прогреться в течение 3 – 5 мин.
4. Установить следующие параметры выходного сигнала генератора: частота – 20 кГц, напряжение – около 2 В.
5. Установить размах колебаний напряжения генератора на экране осциллографа в пределах примерно 2/3 экрана подбором коэффициента Ку канала вертикального отклонения сигнала осциллографа.
6. Получить устойчивое изображение сигнала генератора на экране.
7. Установить такую длительность развертки, при которой на экране наблюдается 2 – 3 периода исследуемого сигнала.
8. Отрегулировать окончательно вертикальный размер изображения сигнала генератора на экране осциллографа с помощью ручки плавной регулировки выходного напряжения генератора.
Задание 1. Изучение электрических процессов в цепи, содержащей два резистора.
1. Замкнуть с помощью кнопочного переключателя на панели кассеты ФПЭ – 09/ПИ ветвь, содержащую резистор R 1.
2. Получить на экране осциллографа устойчивое изображение двух исследуемых сигналов. Вращая ручку усилителя осциллографа «Вольт/дел», установить вертикальный размер сигнала в пределах 2/3 экрана.
3. Зарисовать наблюдаемые колебания на миллиметровой бумаге. Убедиться, что угол сдвига фаз между током в цепи и входным напряжением равен нулю.
4. Произвести измерение амплитуд напряжений на входе и выходе цепи. Для этого измерить величину амплитуды каждого сигнала в делениях шкалы экрана и умножить полученные значения на коэффициент К У канала вертикального отклонения осциллографа, который соответствует положению ручки усилителя «Вольт/дел». Все результаты записать в табл. 19.1.
Таблица 19.1
| U 01 | U 02 | 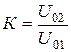
| R 1 Ом | φ град. | ||||
| U 01, дел | КУ, В/дел | U 01, B | U 02, дел | КУ, В/дел | U 02, B | |||
5. Рассчитать значение коэффициента передачи цепи К по формуле (19.19).
6. Определить величину сопротивления резистора R 1 из формулы (19.24):
 , (19.33)
, (19.33)
где R 2=20 кОм.
7. Данные измерений и вычислений занести в таблицу 19.1.
Задание 2. Изучение электрических процессов в цепи, содержащей резистор и конденсатор.
1. Замкнуть с помощью кнопочного переключателя на панели кассеты ФПЭ – 09 ветвь, содержащую конденсатор С.
2. Получить на экране осциллографа устойчивое изображение двух исследуемых сигналов, отрегулировать из размеры.
3. Зарисовать колебания, наблюдаемые на экране осциллографа при частоте генератора 10 кГц.
4. Определить угол сдвига фаз между током в цепи и выходным напряжением при частоте 10 кГц. Для этого измерить в делениях шкалы экрана осциллографа сдвиг во времени ∆ t между изображениями двух исследуемых сигналов и период колебаний Т (рис. 19.6). Разность фаз рассчитать по формуле
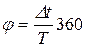 (град). (19.34)
(град). (19.34)

Рис. 19.6.
5. Повторить пункты 3 и 4 при частоте генератора 70 кГц.
6. Провести измерение амплитуд напряжений на выходе и входе цепи при различных значениях частоты генератора ν (по методике, описанной в пункте 4 задания 1). Частоту генератора менять в пределах от 10 до 70 кГц сначала с интервалом 5 кГц (до 30 кГц), а затем с интервалом 10 кГц.
7. Рассчитать значение коэффициента передачи цепи К по формуле (19.19) для всего исследованного диапазона частот.
8. Построить график зависимости коэффициента передачи цепи RC от частоты выходного напряжения К = f (ν).
9. С помощью графика К = f (ν) оценить величину емкости конденсатора С. Для этого воспользоваться линейным участком графика, который описывается формулой (19.28). Определив тангенс угла наклона линейного участка и приравняв его угловому коэффициенту зависимости (19.28), получим соотношение  , откуда
, откуда 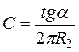 .
.
10. Рассчитать разность фаз φ по формуле (19.26) при двух значениях частоты генератора: 10 и 70 кГц. Сравнить результаты расчета с результатами непосредственного измерения угла φ.
11. Данные измерений и вычислений занести в таблицу 19.2.
Задание 3. Изучение электрических процессов в цепи, содержащей резистор и катушку индуктивности.
1. Замкнуть с помощью кнопочного переключателя на панели кассеты ФПЭ – 09 ветвь, содержащую катушку индуктивности L.
2. Ручкой осциллографа «Уровень» получить на экране устойчивое изображение двух исследуемых сигналов.
Таблица 19.2
| ν, 103, Гц | U 01 | U 02 | 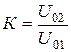
| С, Ф | ∆ t, дел. | Т, дел. | φизм, град. | φрасч, град. | ||||
| U 01, дел | КУ, В/дел. | U 01, В | U 02, дел. | КУ, В/дел. | U 02, В | |||||||
| - | - | |||||||||||
| - | - | |||||||||||
| - | - | |||||||||||
| - | - | |||||||||||
| - | - | |||||||||||
3. Зарисовать колебания, наблюдаемые на экране осциллографа при частоте генератора 30 кГц.
4. Определить угол сдвига фаз между током в цепи и входным напряжением при частоте 30 кГц. Для этого измерить в делениях шкалы экрана осциллографа сдвиг во времени ∆ t между изображениями двух исследуемых сигналов и период колебаний Т (см. на рис. 19.6). Разность фаз рассчитать по формуле (19.34). Данные занести в таблицу 19.3.
5. Повторить пункты 3 и 4 при частоте генератора 100 кГц.
6. Провести измерение амплитуд на входе и выходе цепи при различных значениях частоты генератора ν (по методике, описанной в пункте 4 задания 1). Частоту генератора менять в пределах от 30 до 100 кГц с интервалом 10 кГц.
7. Рассчитать значения коэффициента передачи цепи К по формуле (19.19) для всего исследованного диапазона частот.
8. Построить график зависимости  .
.
9. С помощью графика  оценить величину индуктивности катушки L. Для этого воспользоваться линейным участком графика, который описывается формулой (19.32). Определив тангенс угла наклона линейного участка и приравняв его угловому коэффициенту зависимости (19.19), получим соотношение
оценить величину индуктивности катушки L. Для этого воспользоваться линейным участком графика, который описывается формулой (19.32). Определив тангенс угла наклона линейного участка и приравняв его угловому коэффициенту зависимости (19.19), получим соотношение  , откуда
, откуда  .
.
10. Рассчитать разность фаз φ по формуле (19.30) при двух значениях частоты генератора: 30 и 100 кГц. Сравнить результаты расчета с результатами непосредственного измерения угла φ.
11. Данные измерения и вычислений занести в таблицу 19.3.
Таблица 19.3
| ν, кГц | 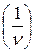 10-5 с
10-5 с
| U 01 | U 02 | 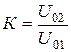
| L, Гн | ∆ t, дел. | Т, дел. | φизм, град. | φрасч, град | ||||
| U 01, дел. | КУ, В/дел. | U 01, В | U 02, дел. | КУ, В/дел. | U 02, В | ||||||||
| - | - | ||||||||||||
| - | - | ||||||||||||
| - | - | ||||||||||||
| - | - | ||||||||||||
| - | - | ||||||||||||
| - | - |
Контрольные вопросы
1. Какой ток называется квазистационарным? Напишите условие квазистационарности.
2. Выведите дифференциальное уравнение вынужденных колебаний, используя второе правило Кирхгофа.
3. Получите выражение: а) для емкостного сопротивления; б) для индуктивного сопротивления.
4. Чему равен сдвиг фаз между током и напряжением на емкостном сопротивлении? На индуктивном?
5. В чем заключается метод векторных диаграмм?
6. Используя метод векторных диаграмм, выведите формулы (19.15), (19.16) и (19.17).
7. Постройте векторную диаграмму для цепи, содержащей последовательно соединенные: а) R и С; б) R и L. Определите с помощью векторной диаграммы для каждой цепи сопротивление Z и сдвиг фаз между током и ЭДС.
8. Получите выражение для коэффициента передачи для схемы, состоящей: а) из R и С; б) из R и L.
9. Как в работе проводится оценка: а) величины емкости конденсатора С; б) величины индуктивности катушки L?
&n






