1. Перед началом выполнения работы ознакомиться с установкой и проверить правильность включения приборов.
2. Включить установку в сеть тумблером 1.
3. Установить рукояткой 4 анодное напряжение U a по заданию преподавателя. Значение U а записать в табл.17.3.
4. Изменяя поворотом ручки 5 ток в катушке, подобрать такой I кр, при котором зеленое поле индикатора 6Е5С отрывается от края экрана (полностью перестает касаться внешней окружности). Значения I кр записать в таблицу 17.3.
Таблица 17.3
| Номер опыта | U a, В, | I кр., А | (e/m), Кл/кг | (e/m)ср., Кл/кг, | Δ(e/m), Кл/кг | (e/m)табл., Кл/кг |
5. Произвести измерения при других значениях напряжения, заданных преподавателем.
6. Произвести вычисления удельного заряда по формуле (17.15), где m 0 =4p×10-7 Гн/м – магнитная постоянная; L =0.1м; r a=0.01м, N = 370; K = 0.85;  – анодное напряжение;
– анодное напряжение; 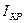 – критический ток.
– критический ток.
7. Рассчитать среднее значение удельного заряда и его погрешность, сравнить с табличным значением.
8. Результаты расчетов занести в таблицу 17.3.
9. Сделать выводы.
Контрольные вопросы.
1. Напишите формулу силы Лоренца в векторном и скалярном виде. Как направлена сила Лоренца?
2. Рассмотрите движение электрона в однородном магнитном поле в двух случаях: а) скорость электрона 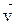 ^
^ 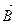 ; б) скорость электрона
; б) скорость электрона 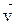 направлена под углом a к полю
направлена под углом a к полю  (найти радиус траектории, период вращения, шаг винтовой линии).
(найти радиус траектории, период вращения, шаг винтовой линии).
3. В чем суть метода магнетрона для определения удельного заряда?
4. Выведите расчетную формулу (17.12).
5. Влияет ли на величину Вкр изменение направления тока в соленоиде на противоположное?
6. Нарисуйте траекторию электрона на участке "катод-анод". Укажите векторы сил, действующих на электрон.
Используемая литература
[1] § 21.2, 23.1, 23.3;
[2] §§ 14.2, 14.3;.
[3] §§ 2.41, 2.42;
[4] т.2, §§ 43, 72, 74, 75;
[5] §§ 114, 115.
Лабораторная работа 2-18
Исследование затухающих колебаний в колебательном контуре (ФПЭ-10)
Цель работы: изучение затухающих электромагнитных колебаний; оценка влияния параметров реального колебательного контура на характеристики затухания; отображение колебательных процессов на фазовой плоскости.
Теоретическое введение
Колебаниями называются процессы, характеризуемые повторяемостью во времени. Колебания, вызванные сообщением начального запаса энергии, называются свободными или собственными. Собственная частота колебательной системы w 0 определяется только параметрами системы.
Затухающими называются колебания, амплитуда которых уменьшается во времени, что объясняется потерями энергии в процессе свободных колебаний.
|
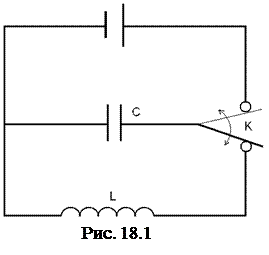 Если зарядить конденсатор от батареи до напряжения U 0 (рис. 18.1), а затем повернуть переключатель К, то конденсатор начнет разряжаться через катушку и в контуре возникнут электромагнитные колебания. Рассмотрим, как происходят эти колебания в контуре, сопротивление которого R =0. При замыкании контура в нем появляется ток I, создающий магнитное поле. Изменение магнитного поля тока приводит к возникновению в цепи электродвижущей силы самоиндукции ε i, замедляющей быстроту разряда. При уменьшении тока возникает электродвижущая сила, направленная в ту же сторону, что и вызвавший ее появление ток. Это приводит к тому, что после разряда конденсатора ток не прекращается сразу, а в течение некоторого времени продолжает течь в том же направлении и перезаряжает обкладки конденсатора. Затем процесс разряда начинается снова, но протекает теперь в обратном направлении. В результате вторичной перезарядки конденсатора система возвращается в исходное состояние, после чего происходит повторение тех же процессов. Время, в течение которого конденсатор заряжается и разряжается, называется периодом собственных колебаний.
Если зарядить конденсатор от батареи до напряжения U 0 (рис. 18.1), а затем повернуть переключатель К, то конденсатор начнет разряжаться через катушку и в контуре возникнут электромагнитные колебания. Рассмотрим, как происходят эти колебания в контуре, сопротивление которого R =0. При замыкании контура в нем появляется ток I, создающий магнитное поле. Изменение магнитного поля тока приводит к возникновению в цепи электродвижущей силы самоиндукции ε i, замедляющей быстроту разряда. При уменьшении тока возникает электродвижущая сила, направленная в ту же сторону, что и вызвавший ее появление ток. Это приводит к тому, что после разряда конденсатора ток не прекращается сразу, а в течение некоторого времени продолжает течь в том же направлении и перезаряжает обкладки конденсатора. Затем процесс разряда начинается снова, но протекает теперь в обратном направлении. В результате вторичной перезарядки конденсатора система возвращается в исходное состояние, после чего происходит повторение тех же процессов. Время, в течение которого конденсатор заряжается и разряжается, называется периодом собственных колебаний.В начальный момент, когда конденсатор полностью заряжен, в нем накоплена электрическая энергия: 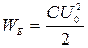 . Во время разрядки конденсатора электрическая энергия превращается в энергию магнитного поля катушки, и когда конденсатор полностью разряжен, вся электрическая энергия переходит в магнитную:
. Во время разрядки конденсатора электрическая энергия превращается в энергию магнитного поля катушки, и когда конденсатор полностью разряжен, вся электрическая энергия переходит в магнитную:
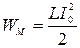 ,
,
где I 0 – наибольшая величина тока в контуре.
При перезарядке конденсатора энергия магнитного поля снова превращается в энергию электрического поля. В контуре возникают незатухающие электромагнитные колебания.
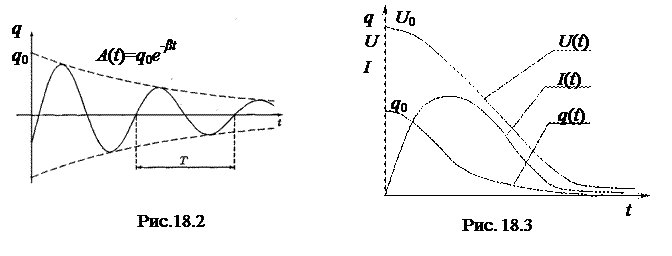
Проводники контура всегда обладают электрическим сопротивлением, поэтому часть энергии в процессе колебаний расходуется на нагрев проводников. Вследствие этого амплитуда электромагнитных колебаний в контуре постепенно уменьшается, и в нем происходят затухающие колебания (рис. 18.2). При достаточно большом сопротивлении контура или малой индуктивности колебания в нем вообще не возникают, а происходит так называемый апериодический разряд конденсатора (рис. 18.3).
По второму закону Кирхгофа можно записать:
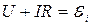 ; (18.1)
; (18.1)
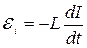 , (18.2)
, (18.2)
где
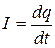 . (18.3)
. (18.3)
Так как  , то из (18.1), (18.2) и (18.3) получаем:
, то из (18.1), (18.2) и (18.3) получаем:
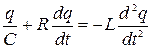 .
.
Или после деления на L:
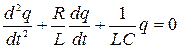 . (18.4)
. (18.4)
Полученное уравнение (18.4) является однородным дифференциальным уравнением второго порядка, оно описывает затухающие колебания. Приняты следующие обозначения:
 ,
, 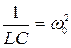 , (18.5)
, (18.5)
тогда уравнение можно записать в стандартном виде:
 , (18.4 а)
, (18.4 а)
здесь β – коэффициент затухания, w 0 – частота собственных незатухающих колебаний контура (то есть частота свободных колебаний контура при отсутствии сопротивления R).
При не слишком большом затухании, то есть если β < w 0, решение уравнения (18.4) имеет вид:
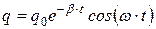 , (18.6)
, (18.6)
где циклическая частота затухающих колебаний ω равна:
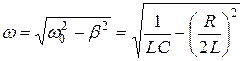 , (18.7)
, (18.7)
а амплитуда стечением времени уменьшается по экспоненте (рис.18.2):
A (t)= q 0 e - βt. (18.8)
При этом период колебаний
 . (18.9)
. (18.9)
Из (18.6) найдем напряжение на конденсаторе:
 , (18.10)
, (18.10)
Если (18.1) записать в виде: 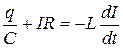 и продифференцировать по времени, то получим уравнение того же типа, что и уравнение (18.4):
и продифференцировать по времени, то получим уравнение того же типа, что и уравнение (18.4):
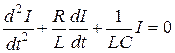 , (18.4 б)
, (18.4 б)
из чего следует, что ток в контуре также совершает затухающие колебания, для которых значения β, ω и Т определяются по формулам (18.5), (18.7) и (18.8):
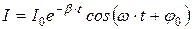 . (18.11)
. (18.11)
Тот же результат можно получить, продифференцировав по времени (18.6):
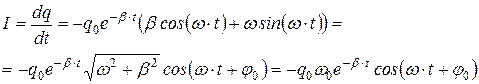 (18.12)
(18.12)
Из формул (18.7) и (18.8) следует, что в контуре возможны затухающие колебания лишь в том случае, если 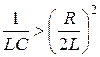 (частота и период – действительные величины), или
(частота и период – действительные величины), или 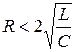 . Если
. Если 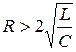 , то частота и период – мнимые, колебаний нет, и происходит апериодический разряд конденсатора (см. рис. 18.3).
, то частота и период – мнимые, колебаний нет, и происходит апериодический разряд конденсатора (см. рис. 18.3).
Сопротивление
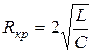 (18.13)
(18.13)
называется критическим.
Для характеристики степени затухания колебаний, кроме коэффициента затухания β, используется еще логарифмический декремент затухания.
Логарифмический декремент затухания – это натуральный логарифм отношения амплитуд двух следующих друг за другом колебаний:
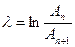 , (18.14)
, (18.14)
где колебания с номерами n и (n+ 1) отстоят друг от друга по времени на один период:
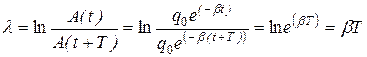 . (18.15)
. (18.15)
Очевидно, логарифмический декремент будет одинаков и для колебаний напряжения, и тока, и заряда на конденсаторе в нашем колебательном контуре, то есть:
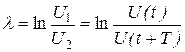 (18.16)
(18.16)
или
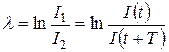 . (18.16 а)
. (18.16 а)
Так как 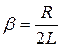 (18.5), то:
(18.5), то:
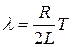 . (18.17)
. (18.17)
Еще одна важная физическая величина характеризует затухание колебаний – добротность:
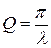 . (18.18)
. (18.18)
Можно показать, что добротность обратно пропорциональна относительной убыли энергии колебаний за время, равное одному периоду:
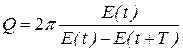 . (18.19)
. (18.19)
В ряде случаев удобно изучать колебательный процесс в системе координат I и U, то есть откладывать по оси абсцисс величину тока в контуре в заданный момент времени, а по оси ординат – напряжение на конденсаторе в тот же момент времени. Плоскость U–I носит название плоскости состояний или фазовой плоскости, а кривая, изображающая зависимость напряжения от тока, называется фазовой кривой.
Найдем фазовую кривую для контура, сопротивление которого R =0. В этом случае  и из (18.7), (18.10) и (18.12) имеем:
и из (18.7), (18.10) и (18.12) имеем:
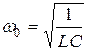 и
и  (18.20)
(18.20)
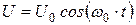 ; (18.21)
; (18.21)
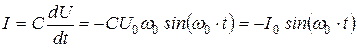 (18.21а)
(18.21а)
Уравнения (18.21) и (18.21а) описывают незатухающие колебания. Исключив из них время t, получим уравнение фазовой кривой:

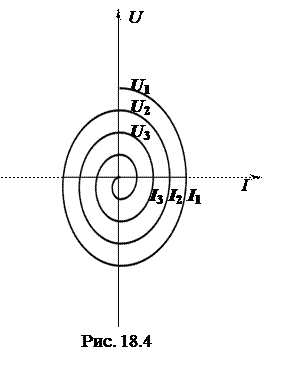
Это уравнение эллипса. Эллипс получается в результате сложения двух взаимно перпендикулярных гармонических колебаний (18.21) и (18.21а), сдвинутых по фазе на четверть периода. В контуре, сопротивление которого R >0, происходят затухающие колебания напряжения (18.10) и тока (18.12). В этом случае амплитуды напряжения и тока в контуре непрерывно убывают, не повторяясь через период времени, и фазовая кривая получается незамкнутой (рис.18.4).
Экспериментальная часть
Приборы и оборудование: генератор звуковых сигналов (PQ); осциллограф (PO); модуль с колебательным контуром (ФПЭ-10); преобразователь импульсов (ФПЭ-08); источник питания (ИП); магазин сопротивлений (МС).






