Экспериментальная установка и методика измерений. Электрическая схема установки представлена на рис.20.5

Электрическая схема установки представлена на рис.20.5. Схема расположения приборов на панельном щитке представлена на рис. 20.6: Щ 4313 – цифровые приборы для измерения силы тока и напряжений; Г6-7 – генератор звуковых колебаний; 1 – тумблер для включения установки в сеть; 2 – индикатор включения; 3 – переключатель вольтметра; C₁, C₂, L₁, L₂ – тумблеры для включения в цепь различных колебательных контуров.

НА ВЕРХНЕМ ПРИБОРЕ Щ 4313 – должны быть нажаты кнопки: "пит", "~", "V", "50", остальные отжаты. Прибор используется для измерения напряжения U _С или U _Г, в зависимости от положения тумблера 3.

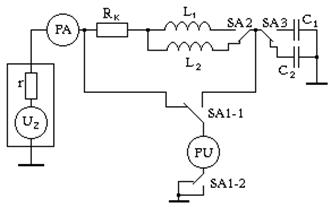
Рис. 20.5

НА НИЖНЕМ ПРИБОРЕ Щ 4313 – должны быть нажаты кнопки: "пит", "~ ", "mA", "50", остальные отжаты. Прибор используется для измерения силы тока.

Рис. 20.6

НА ГЕНЕРАТОРЕ – переключатель формы сигналов – "~", переключатель "множитель" – в положении "10", крайний правый регулятор – на второй точке после нуля.

Перед началом выполнения работы ознакомьтесь с установкой и проверьте правильность включения приборов. Заполните метрологическую карту.

Порядок выполнения работы

1. Включите установку в сеть.

2. Установите на приборном щитке переключатели С и L в одно из положений: C1, L1; C2,L2; C2, L1; C1, L2 по заданию преподавателя.

3. Включите генератор тумблером "сеть".

При измерении частоты генератором имейте в виду: переключателем "множитель" частота сигнала меняется ступенчато, а регулятором, касающимся круга со шкалой – плавно. Величина измеряемой частоты будет равна произведению показания по шкале на круге и показания переключателя "множитель".

4. Изменяя частоту генератора в интервале от 100 до 4000 Гц, определите значение частоты, при которой наблюдается максимальное значение силы тока. Запишите резонансную частоту n₀ и максимальную силу тока I _max в таблицу 20.1.

Таблица 20.1.

n₀, Гц	I _max, mA	I (n_max)≈ I (n_min)≈0.5¸0.6 I _max, mA.	n_min, Гц	n_max, Гц

5. Найдите для исследуемого контура диапазон частот, в котором необходимо произвести измерения. Для этого определите две частоты n_max и n_min: большую и меньшую резонансной, при которых значение тока составляет примерно половину от максимального: I (n_max)≈ I (n_m_in)≈0.4¸0.6 I _max.

6. В интервалах n_min ¸n_рез и n_рез ¸n_max возьмите по 10¸12 значений частоты и измерьте для каждой из них ток в контуре I, напряжение на конденсаторе U_C, напряжение на генераторе U _Г. Результаты запишите в таблицу 20.2.

Таблица 20.2

Параметры системы	№	n, Гц	I, мА	U _С, B	U _Г, B	w, с^-1
C_i, L_i

Например, наибольшее значение силы тока I _max=9 мA достигается при частоте n₀≈2.9^.10³Гц. Вычисляем I (n_max)≈ I (n_m_in)≈0.4¸0.6 I _max≈4 мA. Уменьшая частоту, находим такое её значение n_m_in, при котором сила тока станет 4 мA. Далее увеличиваем частоту от n₀ и находим такое её значение n_max, при котором также сила тока примерно равна 4 мA. Пусть n_m_in≈1^.10³Гц, n_max≈7^.10³Гц, тогда целесообразно производить измерения для следующих частот: 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.4, 2.6, 2.8, 2.9, 3.0, 3.2, 3.4, 3.6, 4.0, 4.5, 5.0, 5.5, 6.0, 7.0 (кГц).

Помните, что приборы измеряют действующее (или эффективное) значение токов и напряжений.

7. Вычислите циклическую частоту w =2pn для всех значений n.

8. По заданию преподавателя повторите измерения, сделанные по пунктам 4, 5, 6, 7 для других контуров.

9. Результаты измерений занесите в таблицу 20.2.

10. Постройте графики зависимостей I = f (w); U _C= f (w) и U _Г= f (w), причем последние два графика обязательно строить в одних и тех же осях.

11. Из графиков зависимости U _C= f (w) и U _Г= f (w) определите e, U _C(w ₀) и U _Г(w ₀) (см.рис.20.4).

12. Из графика зависимости I=f (w) найдите w ₀, D w и I (w ₀) (см.рис.20.3).

13. Рассчитайте активное сопротивление всей цепи R, сопротивление генератора r и активное сопротивление колебательного контура R _К:

14. Найдите величину индуктивности катушки L и емкости конденсатора С (см.формулы (20.4) и (20.30)):

15. Вычислите добротность колебательного контура двумя способами по следующим формулам и сравните результаты (см.формулу (20.29)):

16. Результаты всех вычислений запишите в таблицу 20.3. Сделайте выводы.

Таблица 20.3.

w ₀, с^-1

e, В

U _C(w ₀), В

U _Г(w ₀), В

I (w ₀), мА

D w, с^-1

R, Ом

r, Ом

R _К, Ом

L, Гн

C, Ф

Контрольные вопросы

1. Какие процессы называются электромагнитными колебаниями? Что такое колебательный контур? Дайте понятие свободных и вынужденных электромагнитных колебаний.

2. Запишите дифференциальное уравнение для свободных колебаний в колебательном контуре и его решение. Рассмотрите два случая: идеальный колебательный контур (R =0) и контур, сопротивление которого R ≠0 Проанализируйте их.

3. Какую величину называют коэффициентом затухания, логарифмическим декрементом затухания? В чем их физический смысл?

4. Выведите дифференциальное уравнение, описывающее вынужденные электромагнитные колебания и запишите его решение.

5. Как зависят от времени ток в цепи, напряжение на конденсаторе и его заряд при вынужденных колебаниях? Нарисуйте графики этих зависимостей.

6. От чего зависит амплитуда вынужденных колебаний? Какое явление называется резонансом и какова его роль?

7. При каком значении частоты сила тока в цепи максимальна? При каком значении частоты максимален заряд конденсатора? Напряжение на конденсаторе?

8. Дайте определение добротности колебательного контура. От чего зависит добротность? Как отличаются резонансные кривые для контуров с различной добротностью?

9. Почему добротность является важнейшей характеристикой резонансных свойств и как она определяется в работе?

10. Докажите формулы (20.27) и (20.28).

Используемая литература

[1] §§ 28.1-28.3;

[2] §§ 19.1, 19.6, 19.7;

[3] §§ 3.7, 3.8, 3.10;

[4] т.2, §§ 89-91;

[5] §§ 143, 146-150.

Лабораторная работа 2-21

Изучение явления взаимной индукции (ФПЭ-05)

Цель работы: исследование явления взаимной индукции двух коаксиально расположенных (соосных) катушек.

Теоретическое введение

Рассмотрим два контура 1 и 2, расположенные на некотором расстоянии друг от друга (рис. 21.1). Если по контуру 1 пропустить ток I ₁, то он создает поток магнитной индукции через контур 2, который будет пропорционален току I ₁:

(21.1)

Коэффициент пропорциональности М ₂₁называется коэффициентом взаимной индукции контуров или взаимной индуктивностью контуров. Он зависит от формы и взаимного расположения контуров 1 и 2, а также от магнитных свойств окружающей среды. При изменении тока в первом контуре магнитный поток через второй контур изменяется, следовательно, в нем наводится ЭДС взаимной индукции. Вычислим её с помощью закона Фарадея: ЭДС индукции в замкнутом контуре равна по величине и противоположна по знаку быстроте изменения магнитного потока через поверхность, натянутую на данный контур.

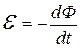. (21.2)

Формула (21.2) является универсальной и справедлива независимо от того, каким способом будут изменять магнитный поток: изменяя индукцию магнитного поля, либо изменяя площадь контура (деформируя контур), либо изменяя ориентацию контура относительно линий магнитной индукции. Более того, формула (21.2) справедлива и для незамкнутого проводника, тогда под dФ нужно понимать пересеченный магнитный поток при движении проводника.

Знак «–» в (21.2) связан с законом сохранения энергии и означает, что индукционный ток всегда имеет такое направление, что его магнитное поле препятствует изменению магнитного потока, вызвавшему индукционный ток. Это – правило Ленца. Таким образом, ЭДС индукции во втором контуре (рис.21.1) равна:

. (21.3)

Формула (21.3) справедлива в отсутствие ферромагнетиков. Если поменять местами контуры 1 и 2 и провести все предыдущие рассуждения, то получим:

(21.4)

Можно показать, что коэффициенты взаимной индукции равны:

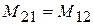. (21.5)

Экспериментальная часть

Приборы и оборудование: звуковой генератор PQ; электронный осциллограф PO; модуль “взаимоиндукция” ФПЭ-05; вольтметр PV (прибор комбинированный Щ-4313).

Функциональная схема установки представлена на рис. 21.2.

Электрическая принципиальная схема модуля ФПЭ-05 “Взаимоиндукция” представлена на рис. 21.3, где: L₁, L₂ – катушки индуктивности на одной оси; П₁, П₂ – переключатели катушек; Ш – шток со шкалой, показывающей взаимное расположение катушек L₁ и L₂.

Методика измерений

В данной работе измеряется коэффициент взаимной индукции между длинной катушкой 1 (L₁) и короткой катушкой 2 (L₂), которая надевается на катушку 1 и может перемещаться вдоль ее оси. Питание одной из катушек, например 1, осуществляется от генератора звуковой частоты PQ, напряжение с которого

(21.6)

подается через сопротивление R. Вольтметр, подключенный к панели PQ, измеряет действующие значения напряжения . Величина R выбирается таким образом, чтобы выполнялось неравенство

, (21.7)

где L ₁ – индуктивность катушки 1, R ₁ – ее активное сопротивление (R =10 кОм). В этом случае ток, протекающий через катушку 1, можно определить по формуле:

(21.8)

Переменный ток в катушке 1 создает переменную ЭДС взаимной индукции в катушке 2:

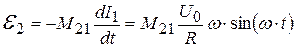. (21.9)

Для измерения используется осциллограф. Амплитуда ЭДС взаимной индукции

, (21.10)

где ν – частота звукового генератора. Из формулы (21.10) имеем:

. (21.11)

Если поменять местами катушки 1 и 2, то можно аналогично измерить

. (21.12)

Экспериментальная установка.

Для изучения явления взаимной индукции предназначена кассета ФПЭ – 05 «Взаимоиндукция», в которой расположены две катушки индуктивности 1 (L₁) и 2 (L₂) на одной оси (рис.21.4) и шток со шкалой (Ш), показывающий взаимное расположение катушек 1 и 2. Принципиальная схема установки показана на рис. 21.2. Для перестановки катушек необходимо переключатели П₁ и П₂ перебросить в противоположное положение. Электрическая схема подключения показана на рис. 21.5. Модуль ФПЭ-05 подключается к звуковому генератору РQ. Вольтметр PV, подключенный к панели РQ, измеряет действующие (эффективные) значения напряжения

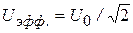(21.13)

Для измерения амплитуды ЭДС взаимной индукции используется электронный осциллограф (РО).

Порядок выполнения работы

Задание 1: Измерение коэффициентов взаимной индукции М₂₁ и М₁₂ и исследование их зависимости от взаимного расположения катушек.

1. Подать напряжение на установку.

2. Ознакомиться с работой электронного осциллографа и звукового генератора.

3. Задать напряжение U _эфф=2 В и частоту сигнала генератора ν=10 кГц, подать напряжение на катушку 1, а ЭДС катушки 2 подать на осциллограф (переключатели П₁ и П₂ в крайнее левое положение). Переключатель “V/дел” на передней панели осциллографа РО установить в положение 0.05 В/дел.

4. Установить подвижную катушку 1 в крайнее переднее положение. Перемещая ее в противоположное крайнее положение через 10 мм, записывать значение координаты Z (расстояние между центрами катушек) и ЭДС взаимной индукции ε ₀₂в цепи катушки 2, измеренную по экрану осциллографа, в табл. 21.1.

5. По формуле (21.11) рассчитать значение М ₂₁. Полученные данные занести в таблицу 21.1.

6. Поменяв местами катушки L₁ и L₂ (оба переключателя П₁ и П₂ в крайнее правое положение), повторить измерения по пунктам 3, 4 и рассчитать М₁₂.

7. Построить графики зависимости М ₂₁ и М ₁₂ как функции координаты Z (расстояние между центрами катушек 1 и 2).

Задание 2: Измерение М₂₁ при различных значениях амплитуды питающего напряжения.

1. Поставить катушку 1 в среднее положение относительно катушки 2. (Выдвинуть шток до положения “50”).

2. Задать частоту звукового генератора PQ ν=20 кГц.

3. Измерить амплитуду ЭДС взаимной индукции ε ₀₂ при различных значениях напряжения U _эфф в цепи катушки 1 в интервале 0÷5 В через 0.4 В.

4. По формуле (21.11) рассчитать М ₂₁. Полученные данные занести в таблицу 21.2.

Таблица 21.1

U _эфф=2 В, ν=10 кГц
Z, мм	e ₀₂	М ₂₁, Гн	e ₀₁	М ₁₂, Гн
дел.	В	дел.	В

Таблица 21.2

ν=20 кГц
U _эфф, В	0.4	0.8	1.2	1.6	2.0	2.4	2.8	3.0	3.4	3.8	4.2	4.6	5.0
e _02,В
М ₂₁, Гн

Таблица 21.3

U _эфф=2.5 В
ν, кГц
e _02,В
М ₂₁, Гн

Задание 3: Измерение М₂₁ при различных частотах питающего напряжения.

1. Поставить катушку 1 в среднее положение относительно катушки 2. (Выдвинуть шток до положения “50”).

2. Задать напряжение звукового генератора U _эфф=2.5 В.

3. Измерить амплитуду ЭДС взаимной индукции ε ₀₂ при различных частотах звукового генератора в интервале (5÷50) кГц через 5 кГц.

4. По формуле (21.11) рассчитать М ₂₁. Полученные данные занести в табл. 21.3.

Контрольные вопросы

1. Сформулируйте закон электромагнитной индукции Фарадея и правило Ленца.

2. Как применить закон Фарадея для определения разности потенциалов на концах прямолинейного проводника, движущегося в магнитном поле?

3. В чем состоит явление взаимной индукции?

4. Чему равна ЭДС взаимной индукции двух контуров?

5. От чего зависит коэффициент взаимной индукции?

6. Выведите расчетные формулы (21.11) и (21.12).

7. Объясните график зависимости М ₂₁= f (Z), полученный в данной работе.

8. Нарисуйте линии магнитного поля катушки индуктивности.

9. Нарисуйте линии магнитного поля системы катушек 1 и 2 для различного положения катушки 1 относительно катушки 2 (см.рис.21.4).

Используемая литература

[1] §§ 25.1, 25.3;

[2] § 17.2;

[3] § 2.46;

[4] т.2, §§ 50, 66;

[5] §§ 123, 128.

Лабораторная работа 2-22

Электростатика

Цель работы: определение емкости проводников с помощью электрометра.

Теоретическое введение

Электроемкость уединенного проводника - это одна из его характеристик, которая показывает, какой заряд нужно сообщить данному проводнику, чтобы его потенциал изменился на единицу, и определяется по формуле:

, (22.1)

где C - емкость проводника; j - потенциал, который получил проводник при сообщении ему заряда q.

Электроемкость проводника зависит от его размеров, формы, наличия по соседству других проводников и от диэлектрической проницаемости среды.

Единицей электроемкости в системе СИ является 1 Фарад - это электроемкость такого проводника, потенциал которого при сообщении заряда в 1 Кулон изменяется на 1 Вольт.

Ёмкость проводника сферической формы радиуса R можно найти, если учесть, что электростатическое поле такого заряженного проводника сферически симметрично и при такое же, как поле точечного заряда, расположенного в центре сферы:

; .

Следовательно, потенциал поверхности сферы равен

и из (22.1) получим:

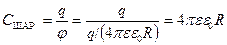. (22.2)

Конденсатором называется совокупность двух любых проводников, способных накапливать энергию электрического поля между обкладками.

Емкость конденсатора определяется отношением заряда на одной из его обкладок к разности потенциалов между обкладками:

. (22.3)

В большинстве случаев форма обкладок конденсатора и их взаимное расположение подбирают таким образом, чтобы внешние поля существенно не влияли на электрическое поле между ними и силовые линии, начинающиеся на одной из обкладок, обязательно заканчивались на другой. Благодаря этому всегда обеспечивается равенство абсолютных значений зарядов на обкладках.

К простейшим типам конденсаторов относятся плоские, сферические и цилиндрические.

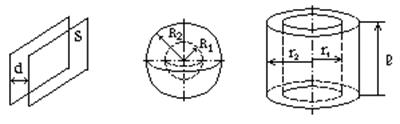Рис.22.1 Рис.22.2 Рис.22.3

Емкость приведенных на рисунках 22.1–22.2 конденсаторов может быть рассчитана по формулам:

плоский конденсатор (рис. 22.1):

; (22.4)

сферический конденсатор (рис. 22.2):

; (22.5)

цилиндрический конденсатор (рис. 22.3):

(22.6)

Для вычисления разности потенциалов на обкладках конденсатора воспользуемся формулой связи напряженности электростатического поля и потенциала: ; или, то же самое в интегральной форме: . Интегрировать здесь будем по радиус-вектору, проведенному от внутренней обкладки к внешней. Вектор напряженности поля направлен радиально (в силу симметрии), тогда

. (22.7)

Напряженность поля между обкладками можно найти по теореме Остроградского-Гаусса (22.8), согласно которой поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охваченных поверхностью, деленной на εε ₀:

. (22.8)

В качестве Гауссовой поверхности в нашем случае следует взять сферу, концентрическую обкладкам, радиусом r: R ₁< r < R ₂. Из-за симметрии напряженность поля в любой точке сферы одинакова и совпадает по направлению с нормалью к поверхности в данной точке, и величину Е можно вынести из под знака интеграла в (22.8), а . В правой части (22.8) суммарный заряд, охваченный Гауссовой поверхностью, - это заряд внутренней обкладки, то есть заряд конденсатора q. Тогда

. (22.9)

Здесь учтено, что - площадь сферы. Выразив Е из (22.8) и подставив в (22.7), получим:

откуда с учетом (22.3) получается (22.5).

Аналогично докажем (22.6). В качестве Гауссовой поверхности здесь следует взять цилиндр, коаксиальный обкладкам цилиндрического конденсатора, радиусом r: r ₁< r < r ₂ и длиной l. Тогда из (22.8) получим:

Далее, из (22.7):

Откуда с учетом (22.3) получим (22.6).

Конденсаторы характеризуются не только их электрической емкостью, но также и напряжением пробоя – такой минимальной разностью потенциалов обкладок, при которой происходит электрический разряд через слой диэлектрика в конденсаторе.

Рис. 22.4

В тех случаях, когда емкости одного конденсатора оказывается недостаточно, конденсаторы соединяют параллельно (рис.22.4). При этом напряжение на конденсаторах оказывается одинаковым: U _i= U. Общий заряд батареи

где n - общее число конденсаторов; q _i - заряд i-го конденсатора. С учетом того, что из (22.3) заряд каждого конденсатора q_i=C _i U _i, где С _i - емкость i-го конденсатора, а общий заряд q=CU,

Рис. 22.5

и после сокращения:

(22.10)

Емкость батареи конденсаторов равна сумме емкостей отдельных конденсаторов.

Последовательно конденсаторы соединяют в том случае, когда их нужно включить в цепь с напряжением выше того, на которое рассчитан отдельный конденсатор. При последовательном соединении конденсаторов (рис. 22.5) заряды на конденсаторах одинаковы: q _i= q, а полное напряжение на батарее равно сумме напряжений:

С учетом (22.3) , , тогда получим:

и после сокращения:

, (22.11)

то есть величина, обратная емкости батареи, равна сумме обратных величин емкостей отдельных конденсаторов.

При последовательном соединении заряды на конденсаторах одинаковы, напряжение на них распределяется в зависимости от их емкостей, что уменьшает возможность пробоя конденсатора.

Экспериментальная часть

Приборы и оборудование: электрометр с заземлённым корпусом, проводники (металлические шары), круглые пластины, цилиндрический конденсатор (коаксиальный кабель), два диэлектрических тела (пластмассовая линейка и целлюлоза).