Таблица 2
| № строки
| № схемы
| А, см2
| k
| H, кН
| b
|
|
|
|
| 1,5
|
| 5 ×10-5
|
|
|
|
| 2,0
|
| 4 ×10-5
|
|
|
|
| 2,5
|
| 3 ×10-5
|
|
|
|
| 3,0
|
| 2 ×10-5
|
|
|
|
| 3,5
|
| 1 ×10-5
|
|
|
|
| 1,5
|
| 5 ×10-5
|
|
|
|
| 2,0
|
| 4 ×10-5
|
|
|
|
| 2,5
|
| 3 ×10-5
|
|
|
|
| 3,0
|
| 2 ×10-5
|
|
|
|
| 3,5
|
| 1 ×10-5
|
|
| в
| а
| е
| д
| б
|
Пример 2. Ступенчатый стальной стержень (рис. 2, а)подвешен в вертикальном положении за верхний конец. При этом нижний конец стержня не доходит до основания на величину  . Требуется без учёта собственного веса: установить, при какой величине силы Н зазор закроется;найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль.
. Требуется без учёта собственного веса: установить, при какой величине силы Н зазор закроется;найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль.
Дано: А = 11 см2; k = 2; c = 12 см; H = 105 кН; 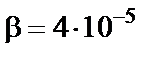 .
.
Решение.
1. Установим, при каком значении силы H зазор закроется. Для этого удлинение стержня приравняем величине зазора:
 ;
;  ;
;
 .
.
2. Найдём реакцию основания при заданном значении H. Для этого удлинение стержня от сил H приравняем сумме зазора и изменения длины стержня от реакции основания:
 ;
;
 .
.
Вычисляем значения продольных сил на участках бруса:
 ;
;
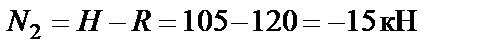 ;
;
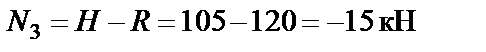 ;
;
 .
.
По найденным значениям строим эпюру продольных усилий (рис. 2, б).
3. Установим, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении H обратилась в нуль. Для этого удлинение стержня от сил H приравняем сумме зазора и изменения длины стержня от температуры:
 ;
;
 °С.
°С.
Задача 3
КРУЧЕНИЕ ВАЛА
Задание.К стальному валу приложены три известных момента: Т 1, Т 2, Т 3 (рис. 3). Требуется: из условия равновесия вала найти значение момента Х (сопротивлением опор пренебречь); построить эпюру крутящих моментов; из расчёта на прочность определить диаметр вала; из расчёта на прочность подобрать вал кольцевого поперечного сечения при заданном отношении внутреннего диаметра d к наружному D; выбрать вал с меньшей площадью поперечного сечения; для выбранного вала построить эпюру углов закручивания, вычислить наибольший относительный угол закручивания  и сравнить его с допускаемым
и сравнить его с допускаемым  = 1 град/м. Данные взятьиз табл. 3.
= 1 град/м. Данные взятьиз табл. 3.
Таблица 3
| №строки
| № схемы
| a, м
| b, м
| c, м
| Т 1, кН×м
| Т 2, кН×м
| Т 3, кН×м
| [t], МПа
| d: D
|
|
|
| 1,1
| 1,1
| 1,1
| 1,1
| 1,1
| 1,1
|
| 0,40
|
|
|
| 1,2
| 1,2
| 1,2
| 1,2
| 1,2
| 1,2
|
| 0,45
|
|
|
| 1,3
| 1,3
| 1,3
| 1,3
| 1,3
| 1,3
|
| 0,50
|
|
|
| 1,4
| 1,4
| 1,4
| 1,4
| 1,4
| 1,4
|
| 0,55
|
|
|
| 1,5
| 1,5
| 1,5
| 1,5
| 1,5
| 1,5
|
| 0,60
|
|
|
| 1,6
| 1,6
| 1,6
| 1,6
| 1,6
| 1,6
|
| 0,65
|
|
|
| 1,7
| 1,7
| 1,7
| 1,7
| 1,7
| 1,7
|
| 0,70
|
|
|
| 1,8
| 1,8
| 1,8
| 1,8
| 1,8
| 1,8
|
| 0,75
|
|
|
| 1,9
| 1,9
| 1,9
| 1,9
| 1,9
| 1,9
|
| 0,80
|
|
|
| 2,0
| 2,0
| 2,0
| 2,0
| 2,0
| 2,0
|
| 0,85
|
|
| е
| а
| б
| в
| г
| д
| е
| а
| в
|
Методические указания
При определении диаметра сплошного вала и наружного диаметра вала кольцевого сечения полученные значения округляют по ГОСТ 6636–69 до ближайшего значения из ряда Rа 40: 10; 10,5; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130; 140; 150; 160 мм.
Пример 3. К стальному валу приложены три известных момента: Т 1, Т 2 и Т 3 (рис. 3, а). Требуется: из условия равновесия вала найти значение момента Х (сопротивлением опор пренебречь); построить эпюру крутящих моментов; определить диаметр вала из расчета на прочность; из расчета на прочность подобрать вал кольцевого поперечного сечения при заданном отношении внутреннего диаметра d к наружному D; выбрать вал с меньшей площадью поперечного сечения; для выбранного вала проверить выполнение условия жесткости (при невыполнении этого условия подобрать размеры поперечного сечения вала из условия жесткости) и построить эпюру углов закручивания.
Дано: a = 1 м; b = 1,5 м; c = 2 м; Т 1 = 3 кН × м; Т 2 = 2 кН × м; Т 3 = 1 кН × м; [t] = 70 МПа; [q] = 1 град/м; d: D = 0,8.
Решение.
1. Из условия равновесия  находим значение момента X:
находим значение момента X:
Т 1+ Т 2– Т 3– X =0;
X= Т 1+ Т 2– Т 3= 3+2 – 1 = 4 кН × м.
2. Вычисляем крутящие моменты на участках вала.
Участок AB: M = T 1=3 кН × м;
Участок BC: M = T 1+ T 2=3+2=5 кН × м;
Участок СD: M = T 1+ T 2– T 3=3+2 – 1=4 кН × м.
По найденным значениям строим эпюру крутящих моментов (рис. 3, б).
Опасным является участок BC, расчётный момент M =5 кН × м.
3. Вычисляем требуемый диаметр вала по условию прочности:
 .
.
Округлив полученное значение, принимаем D =7,5 см.
Находим площадь поперечного сечения (площадь круга):
 .
.
4. Из условия прочности вычисляем внешний диаметр вала кольцевого сечения при заданном соотношении внутреннего и внешнего диаметров  :
:
 см.
см.
После округления полученного значения принимаем D =9,0 см.
Находим площадь поперечного сечения (площадь кольца) при d: D = 0,8 и D = 9 см:
 .
.
5. Для равнопрочных валов сравниваем площади их поперечных сечений 22,89 < 44,16.Выбираем вал кольцевого сечения, как более экономичный.
6. Для выбранного вала проверяем выполнение условия жёсткости. Предварительно вычисляем полярный момент инерции кольца при d: D = 0,8 и D = 9 см:
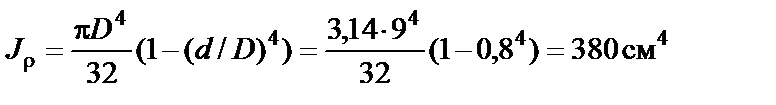 .
.
Находим жёсткость вала при кручении, приняв модуль сдвига стали  МПа:
МПа:
 .
.
Вычисляем наибольший относительный угол закручивания вала:
 .
.
Проверяем условие жёсткости:
 .
.
Условие жёсткости выполняется.
Находим углы закручивания сечений B, C, D относительно сечения А:
 ;
;
 ;
;
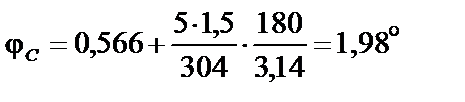 ;
;
 .
.
По вычисленным значениям строим эпюру углов закручивания (рис. 3, в).
Задача 4
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Задание. Для поперечного сечения (рис. 4), требуется: определить положение центра тяжести; найти осевые и центробежный моменты инерции относительно случайных центральных осей; определить направления главных центральных осей; найти моменты инерции относительно главных центральных осей; вычертить сечение в масштабе 1:1 и указать на нём все оси и размеры в числах. Данные взять из табл. 4.
Таблица 4
| № строки
| № сечения
| Швеллер
| Уголок
| Двутавр
|
|
|
|
| 80´80 ´6
|
|
|
|
|
| 80´80 ´8
|
|
|
|
|
| 90´90 ´6
|
|
|
|
|
| 90´90 ´7
|
|
|
|
|
| 90´90 ´8
|
|
|
|
|
| 100´100 ´8
| 20а
|
|
|
|
| 100´100 ´10
|
|
|
|
|
| 100´100 ´12
| 22а
|
|
|
|
| 125´125 ´10
|
|
|
|
|
| 125´125 ´12
| 24а
|
|
| е
| г
| д
| в
|
 . Требуется без учёта собственного веса: установить, при какой величине силы Н зазор закроется;найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль.
. Требуется без учёта собственного веса: установить, при какой величине силы Н зазор закроется;найти реакцию основания при заданном значении силы Н и построить для стержня эпюру продольных усилий; установить, на сколько градусов надо охладить стержень, чтобы реакция основания при заданном значении силы Н обратилась в нуль.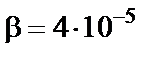 .
. ;
;  ;
; .
. ;
; .
. ;
;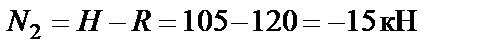 ;
;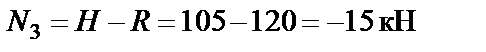 ;
; .
. ;
; °С.
°С. и сравнить его с допускаемым
и сравнить его с допускаемым  = 1 град/м. Данные взятьиз табл. 3.
= 1 град/м. Данные взятьиз табл. 3. находим значение момента X:
находим значение момента X: .
. .
. :
: см.
см. .
.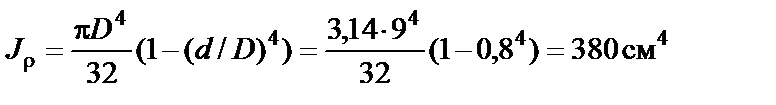 .
. МПа:
МПа: .
. .
. .
. ;
; ;
;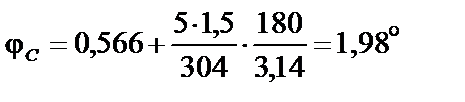 ;
; .
.






