Таблица 8
| № строки
| № схемы
| a
|
|
|
| 1,1
|
|
|
| 1,2
|
|
|
| 1,3
|
|
|
| 1,4
|
|
|
| 1,5
|
|
|
| 0,6
|
|
|
| 0,7
|
|
|
| 0,8
|
|
|
| 0,9
|
|
|
| 1,0
|
|
| е
| д
|
Пример 8.На рис. 8, а изображена в аксонометрии ось ломаного стержня круглого поперечного сечения. На стержень действует вертикальная нагрузка. Требуется: построитьэпюры изгибающих и крутящих моментов; установить опасное сечение и найти для него расчётный момент по III теории прочности.
Решение:
1. В первую очередь необходимо для каждого из стержней назначить оси координат. Обычно ось z направляют вдоль оси каждого участка.
2. Определяем изгибающие моменты  на каждом участке и строим эпюру Мx (рис. 8, б).
на каждом участке и строим эпюру Мx (рис. 8, б).
●Участок EA: z 1Î[0; 1,3  ];
];



●Участок AB: z 2 Î[0;  ];
];
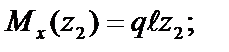


●Участок DB: z 3Î[0;  ];
];

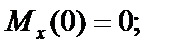

●Участок BC: z 4Î[0; 1,3  ];
];



3. Определяем крутящие моменты  на каждом участке и строим эпюру Мz (рис. 8, в).
на каждом участке и строим эпюру Мz (рис. 8, в).
●Участок EA: 
●Участок AB: 
●Участок DB: 
●Участок BC: 
4. Изгибающие моменты Му на всех участках отсутствуют, так как все силы параллельны оси у.
5. Показываем возможные опасные сечения (рис. 8, г). Вычисляем в них расчётные моменты по III теории прочности  в долях
в долях  и записываем результаты в табл. 8, а.
и записываем результаты в табл. 8, а.
Таблица 8, а
| Сечение
| 
| 
| 
|
|
|
| 0,8
| 1,27
|
|
|
| 0,8
| 1,27
|
|
|
| 1,3
| 1,64
|
|
|
| 1,3
| 1,3
|
|
| 1,3
|
| 1,3
|
|
| 0,5
|
| 0,5
|
Опасным является третье сечение, 
Задача 9
РАСЧЕТ КРИВОЛИНЕЙНОГО СТЕРЖНЯ
Задание.Для криволинейного стержня (рис. 9) построить эпюры M, Q, N и найти нормальные напряжения в опасном сечении. Данные взять из табл. 9. Формы поперечных сечений изображены на рис. 9, а.
Таблица 9
| № строки
| Схема порис.12
| α, °
| P,кН
| r,см
| d,см
| Сечение по рис.12, а
|
|
|
|
| 1,1
|
| 4,1
|
|
|
|
|
| 1,2
|
| 4,2
|
|
|
|
|
| 1,3
|
| 4,3
|
|
|
|
|
| 1,4
|
| 4,4
|
|
|
|
|
| 1,5
|
| 4,5
|
|
|
|
|
| 1,6
|
| 4,6
|
|
|
|
|
| 1,7
|
| 4,7
|
|
|
|
|
| 1,8
|
| 4,8
|
|
|
|
|
| 1,9
|
| 4,9
|
|
|
|
|
| 2,0
|
| 5,0
|
|
|
| а
| б
| в
| г
| д
| е
|
Пример 9:Для криволинейного стержня (рис. 9, б) построить эпюры Q, N, M и найти нормальные напряжения в опасном сечении, если: P = 1,2 кН; r = 16 см;a= 45°.Сечение имеет форму трапеции с размерами: h = 6 см; b 1 = 3 см; b 2 = 6 см (рис. 9, г.) Все размеры на рисунках указаны в сантиметрах.
Решение:
1. Определим вертикальную и горизонтальную составляющие силы Р:


2. Запишем выражения для внутренних сил в произвольном сечении:






Полученные формулы используем для вычисления Q, N, M (табл. 9, а) с шагом углаdj = 30°.
Таблица 9, а
| Величина
| j = 0
| j= 30°
| j= 60°
| j= 90°
| j= 120°
| j= 150°
| j= 180°
|
| Q, кН
| 0,849
| 0,311
| –0,311
| –0,849
| –1,16
| –1,16
| –0,849
|
| N, кН
| 0,849
| 1,16
| 1,16
| 0,849
| 0,31
| –0,31
| –0,849
|
| M, кН × м
|
| 0,0497
| 0,0497
|
| –0,086
| –0,186
| –0,272
|
По данным табл.12, а строим эпюры Q, N и М (рис.9, в).
3. Определим напряжения в опасном сечении (рис.9, г) при следующих значениях внутренних усилий: M = –272 Н × м; N = –849 Н.
Нормальные напряжения вычисляются по формуле:
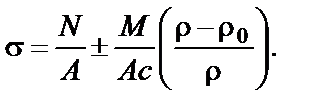
Центр тяжести трапеции находится от основания на расстоянии:

Внутренний и наружный радиусы криволинейного стержня


Радиус кривизны нейтрального слоя для сечения в форме трапеции (при N = 0):


| Нейтральная линия приN = 0
|
Рис. 9, г
Расстояние от центра тяжести до нейтрального слоя (при N = 0) 
Площадь сечения
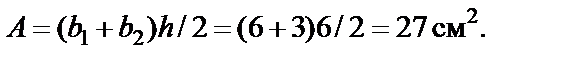
Значения напряжений в характерных точках:
●  :
: 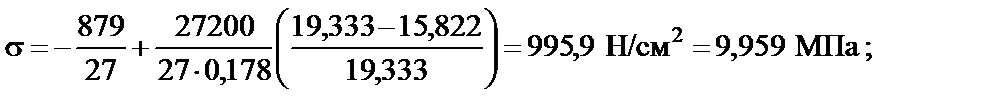
●  :
: 
●  :
: 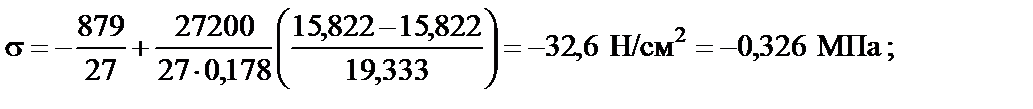
●  :
: 
По полученным значениям строим эпюру s (рис.9, г).
Задача 10
РАСЧЕТ СТЕРЖНЯ НА УСТОЙЧИВОСТЬ
Задание. Стальной стержень (рис. 10) сжимается силой Р. Требуется:найти размеры поперечного сечения (рис. 10, а) при расчетном сопротивлении на простое сжатие R =200 МПа;найти значение критической силы и коэффициент запаса устойчивости. Данные взять из табл. 10.
Таблица 10
| № строки
| Схема закрепления стержня по рис. 13
| Сечение стержня по рис. 13, а
| Р, кН
|  , м , м
|
|
|
|
|
| 2,1
|
|
|
|
|
| 2,2
|
|
|
|
|
| 2,3
|
|
|
|
|
| 2,4
|
|
|
|
|
| 2,5
|
|
|
|
|
| 2,6
|
|
|
|
|
| 2,7
|
|
|
|
|
| 2,8
|
|
|
|
|
| 2,9
|
|
|
|
|
| 3,0
|
|
| е
| а
| в
| г
|
Пример 10:Стальной стержень (рис. 10, б) сжимается силой Р = 400кН. Найти размеры поперечного сечения, значение критической силы и коэффициент запаса устойчивости, если  м, R = 200 МПа.
м, R = 200 МПа.
Решение:
1. Для поперечного сечения определяем площадь А в общем виде, и выражаем размер а через площадь А:


2. Минимальный момент инерции сечения
 .
.
3. Минимальный радиус инерции сечения
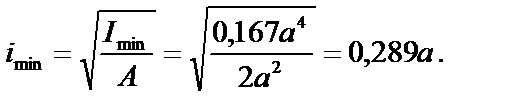
4. Гибкость стержня 
5. Первое приближение  :
:



Для найденной гибкости определяем соответствующий коэффициент продольного изгиба, используя линейную интерполяцию табличных данных:



Вычисляем действующее и допускаемое напряжения:
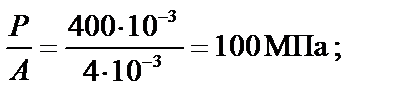


Получили перегрузку, величина которой больше 5%, следовательно, выполняем второе приближение.
6. Второе приближение:










Во втором приближении также имеет место перегрузка, но ее величина стала меньше 5%. Принимаем: 
 .
.
7. Находим критическую силу. Так как  ,расчёт ведем по формуле Эйлера:
,расчёт ведем по формуле Эйлера:


8. Определяем коэффициент запаса

Задача 11
РАСЧЁТ БАЛКИ НА УДАРНУЮ НАГРУЗКУ
Задание. На двутавровую балку, свободно лежащую на двух жестких опорах (рис. 11), с высоты h падает груз Q. Требуется: найти наибольшее нормальное напряжение в балке; решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой (т.е. осадка от груза 1 кН) равна a; сравнить полученные результаты. Данные взять из табл. 11.
Таблица 11
| № строки
| № схемы
| № двутавра
|  м м
| Q, Н
| h, см
| a, м/кН
|
|
|
|
| 2,1
|
|
| 21×10-3
|
|
|
| 20а
| 2,2
|
|
| 22×10-3
|
|
|
|
| 2,3
|
|
| 23×10-3
|
|
|
| 24а
| 2,4
|
|
| 24×10-3
|
|
|
|
| 2,5
|
|
| 25×10-3
|
|
|
| 27а
| 2,6
|
|
| 26×10-3
|
|
|
|
| 2,7
|
|
| 27×10-3
|
|
|
| 30а
| 2,8
|
|
| 28×10-3
|
|
|
|
| 2,9
|
|
| 29×10-3
|
|
|
|
| 3,0
|
|
| 30×10-3
|
|
| е
| д
| в
| а
| г
| б
|
 на каждом участке и строим эпюру Мx (рис. 8, б).
на каждом участке и строим эпюру Мx (рис. 8, б). ];
];


 ];
];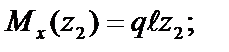


 ];
];
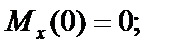

 ];
];


 на каждом участке и строим эпюру Мz (рис. 8, в).
на каждом участке и строим эпюру Мz (рис. 8, в).



 в долях
в долях  и записываем результаты в табл. 8, а.
и записываем результаты в табл. 8, а.











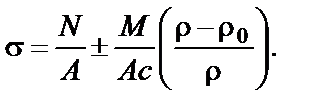






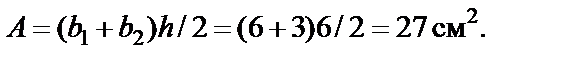
 :
: 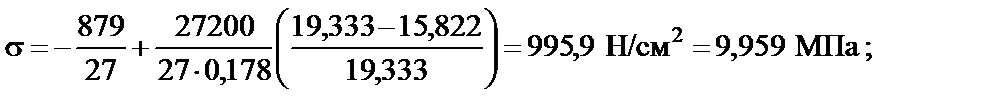
 :
: 
 :
: 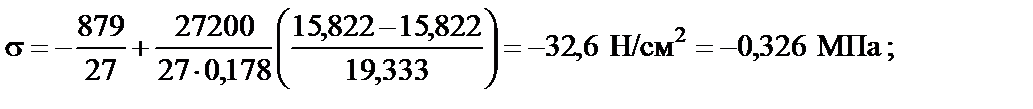
 :
: 
 , м
, м






 м, R = 200 МПа.
м, R = 200 МПа.


 .
.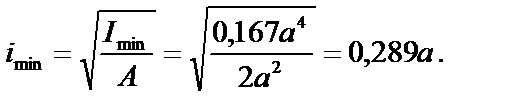

 :
:





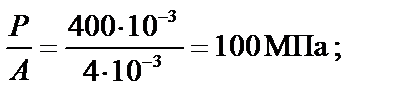













 .
. ,расчёт ведем по формуле Эйлера:
,расчёт ведем по формуле Эйлера:


 м
м






