Методические указания
При наличии упомянутой ранее пружины  , где
, где 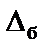 – прогиб балки, лежащей на жестких опорах, в том сечении, где приложена сила Q (при статическом действии этой силы);
– прогиб балки, лежащей на жестких опорах, в том сечении, где приложена сила Q (при статическом действии этой силы);  осадка пружины от реакции, возникающей от силы Q;
осадка пружины от реакции, возникающей от силы Q;  – коэффициент, устанавливающий зависимость между осадкой пружины и перемещением точки приложения силы Q, вызванным поворотом всей балки вокруг центра шарнира левой опоры как жесткого целого (коэффициент
– коэффициент, устанавливающий зависимость между осадкой пружины и перемещением точки приложения силы Q, вызванным поворотом всей балки вокруг центра шарнира левой опоры как жесткого целого (коэффициент 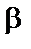 находят из подобия треугольников).
находят из подобия треугольников).
Пример 11: На двутавровую балку (№ 24, Wx = 289 см3, Ix = 3460 см4, l = 4м), свободно лежащую на двух жестких опорах (рис. 11, а), с высоты h = 11 см падает груз Q = 600 Н. Найти наибольшее нормальное напряжение в балке; решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой равна a =  м/кН.
м/кН.
Рис. 11, а
Решение:
1. Определим прогиб балки в точке удара (в точке С) при статическом действии силы Q. Предварительно покажем единичное состояние, построим эпюру изгибающих моментов  (рис.14, б) и вычислим перемещение
(рис.14, б) и вычислим перемещение  от единичной силыпо формуле трапеций:
от единичной силыпо формуле трапеций:
Эпюра 
|
Рис. 11, б


2. Определим динамический коэффициент:

3. Вычислим наибольшие нормальные напряжения в балке при статическом нагружении:

4. Наибольшие нормальные напряжения в балке при ударе

5. Определим напряжения в балке при ударе, если правая опора заменена пружиной (рис.11, в). Предварительно рассмотрим статическое нагружение.
Осадка опоры В

Перемещение точки С, вызванное осадкой опоры В:

Полное перемещение точки С (с учетом осадки опоры В и прогиба балки)

Динамический коэффициент

Наибольшие нормальные напряжения в балке при ударе
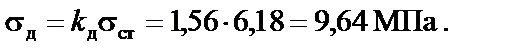
Вывод: после замены жесткой опоры пружиной напряжения в балке при ударе уменьшились в
92,2 / 9,64 = 9,56раз.
Задача 12
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ
Задание. Для балки, изображенной на рис. 12, требуется: построить эпюры Q и M; выполнить статическую и кинематическую проверку; подобрать двутавровое сечение. Данные взять из табл. 12. Принять EJ = const.
Рис. 12
Таблица 12
| № строки
| № схемы
| a, м
| b, м
| c, м
| M, кН × м
| q, кН/м
| P, кН
|
|
|
| 1,1
| 1,1
| 1,1
| 1,1
| 1,1
| 1,1
|
|
|
| 1,2
| 1,2
| 1,2
| 1,2
| 1,2
| 1,2
|
|
|
| 1,3
| 1,3
| 1,3
| 1,3
| 1,3
| 1,3
|
|
|
| 1,4
| 1,4
| 1,4
| 1,4
| 1,4
| 1,4
|
|
|
| 1,5
| 1,5
| 1,5
| 1,5
| 1,5
| 1,5
|
|
|
| 1,6
| 1,6
| 1,6
| 1,6
| 1,6
| 1,6
|
|
|
| 1,7
| 1,7
| 1,7
| 1,7
| 1,7
| 1,7
|
|
|
| 1,8
| 1,8
| 1,8
| 1,8
| 1,8
| 1,8
|
|
|
| 1,9
| 1,9
| 1,9
| 1,9
| 1,9
| 1,9
|
|
|
| 2,0
| 2,0
| 2,0
| 2,0
| 2,0
| 2,0
|
|
| е
| а
| б
| в
| г
| д
| е
|
Методические указания
При решении задачи использовать метод сил. Для вычисления перемещений применять формулы сокращенного перемножения эпюр.
Пример 15: Для балки (рис. 12, а) построить эпюры поперечных сил Q и изгибающих моментов M; выполнить статическую и кинематическую проверку; подобрать двутавровое сечение. Допускаемое напряжение 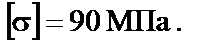
Решение:
1. Находим степень статической неопределимости (число опорных связей минус три) n = 4 – 3=1.
2. Выбираем основную систему в виде балки на двух шарнирных опорах (рис. 12, б).
3. Показываем эквивалентную систему (рис. 12, в).
4. Составляем каноническое уравнение по методу сил:
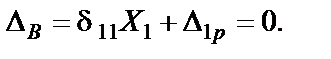
5. Для определения перемещений  и
и  предварительно построим эпюры изгибающих моментов в основной системе при единичном и грузовом состоянии. Перемещения будем искать по формулам перемножения эпюр. Для участков с распределённой нагрузкой необходимо знать моменты на концах и в серединах участков, для участков без распределённой нагрузки достаточно вычислить моменты на концах. Рассмотрим единичное состояние (рис. 12, г). Все размеры даны в метрах.
предварительно построим эпюры изгибающих моментов в основной системе при единичном и грузовом состоянии. Перемещения будем искать по формулам перемножения эпюр. Для участков с распределённой нагрузкой необходимо знать моменты на концах и в серединах участков, для участков без распределённой нагрузки достаточно вычислить моменты на концах. Рассмотрим единичное состояние (рис. 12, г). Все размеры даны в метрах.
Эпюра 
|
Определяем реакции опор:






Проверка:

 –0,5437+1 – 0,4563=1 – 1=0.
–0,5437+1 – 0,4563=1 – 1=0.
Реакции опор найдены верно.
Вычисляем значения  в сечениях балки:
в сечениях балки:
● точка A: 
● точка T: 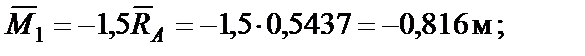
● точка B: 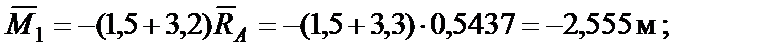
● точка K: 
● точка D: 
●точка R: 
●точка C: 
По найденным значениям строим эпюру  (рис. 12, г).
(рис. 12, г).
Рассмотрим грузовое состояние основной системы (рис. 12 д).
Эпюра 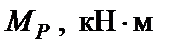
|
Определяем реакции опор:
 ;
; 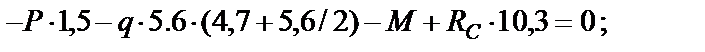
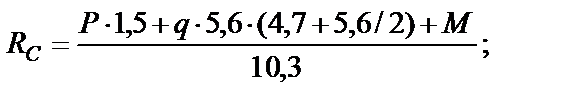
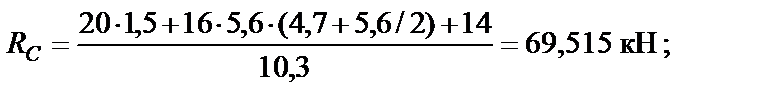

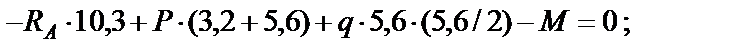


Проверка: 
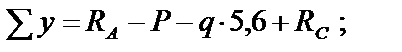

Реакции опор найдены верно.
Вычисляем значения моментов Mp в сечениях:
●точка A: 
●точка T: 
●точка B: 
●точка K: 

●слева от точки D:

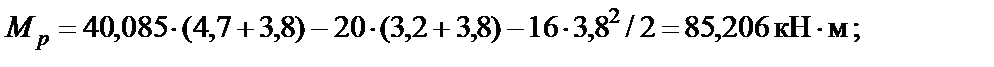
●справа от точки D: 
●точка R: 
●точка C: 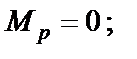
По найденным значениям строим эпюру Mp (рис. 12, д).
Умножаем эпюру  саму на себя:
саму на себя: 

Перемножаем эпюры  и Mp;
и Mp; 




Из уравнения  находим Х 1 :
находим Х 1 :

Строим исправленную эпюру  (рис. 12, е). Для этого все значения эпюры
(рис. 12, е). Для этого все значения эпюры  (рис. 12, г) умножаем на
(рис. 12, г) умножаем на 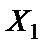 .
.
Строим окончательную эпюру моментов M (рис. 12, е). Для этого складываем эпюры  и
и  .
.
Кинематическая проверка: 
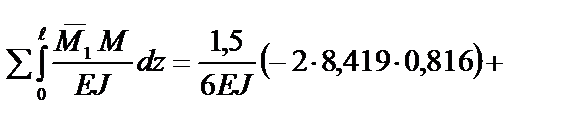
 +
+
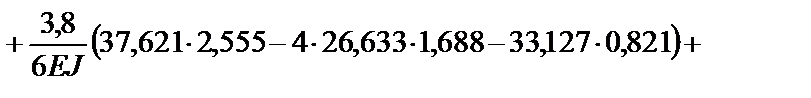

 .
.
Эпюра 
|
Эпюра 
|
Эпюра 
|








 , где
, где 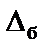 – прогиб балки, лежащей на жестких опорах, в том сечении, где приложена сила Q (при статическом действии этой силы);
– прогиб балки, лежащей на жестких опорах, в том сечении, где приложена сила Q (при статическом действии этой силы);  осадка пружины от реакции, возникающей от силы Q;
осадка пружины от реакции, возникающей от силы Q;  – коэффициент, устанавливающий зависимость между осадкой пружины и перемещением точки приложения силы Q, вызванным поворотом всей балки вокруг центра шарнира левой опоры как жесткого целого (коэффициент
– коэффициент, устанавливающий зависимость между осадкой пружины и перемещением точки приложения силы Q, вызванным поворотом всей балки вокруг центра шарнира левой опоры как жесткого целого (коэффициент 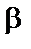 находят из подобия треугольников).
находят из подобия треугольников). м/кН.
м/кН.

 (рис.14, б) и вычислим перемещение
(рис.14, б) и вычислим перемещение  от единичной силыпо формуле трапеций:
от единичной силыпо формуле трапеций:
















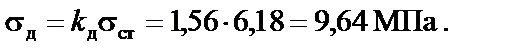
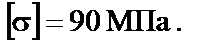

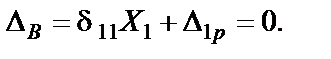
 и
и  предварительно построим эпюры изгибающих моментов в основной системе при единичном и грузовом состоянии. Перемещения будем искать по формулам перемножения эпюр. Для участков с распределённой нагрузкой необходимо знать моменты на концах и в серединах участков, для участков без распределённой нагрузки достаточно вычислить моменты на концах. Рассмотрим единичное состояние (рис. 12, г). Все размеры даны в метрах.
предварительно построим эпюры изгибающих моментов в основной системе при единичном и грузовом состоянии. Перемещения будем искать по формулам перемножения эпюр. Для участков с распределённой нагрузкой необходимо знать моменты на концах и в серединах участков, для участков без распределённой нагрузки достаточно вычислить моменты на концах. Рассмотрим единичное состояние (рис. 12, г). Все размеры даны в метрах.









 –0,5437+1 – 0,4563=1 – 1=0.
–0,5437+1 – 0,4563=1 – 1=0. в сечениях балки:
в сечениях балки:
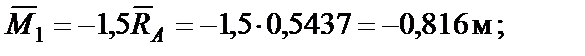
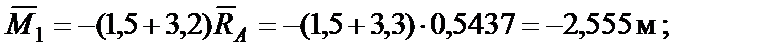




 (рис. 12, г).
(рис. 12, г).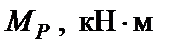
 ;
; 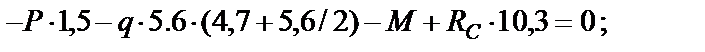
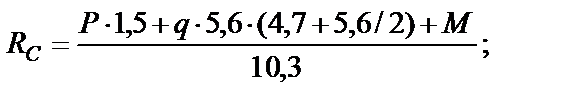
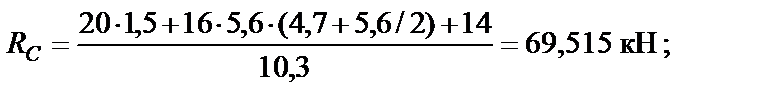

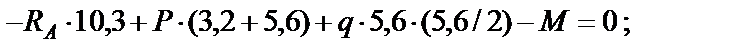



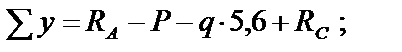







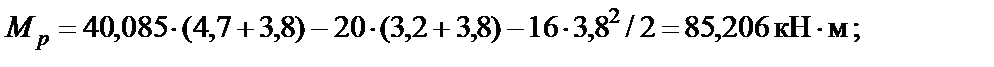


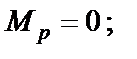
 саму на себя:
саму на себя: 

 и Mp;
и Mp; 




 находим Х 1 :
находим Х 1 :
 (рис. 12, е). Для этого все значения эпюры
(рис. 12, е). Для этого все значения эпюры  (рис. 12, г) умножаем на
(рис. 12, г) умножаем на 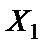 .
. и
и  .
.
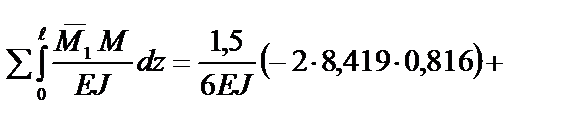
 +
+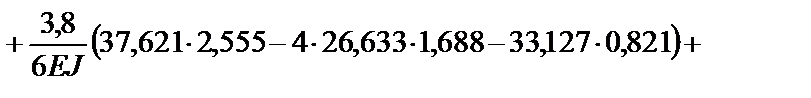

 .
.








