СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ РАМА
Задание.Для рамы (рис. 6) требуется написать выражения для продольных сил N, поперечных сил Q и изгибающих моментов M на каждом участке в общем виде, построить эпюры N, Q, M и подобрать двутавровое сечение при R =220МПа. Данные взять из табл. 6.
Таблица 6
| № строки
| № схемы
| a, м
| b, м
| c, м
| M, кН × м
| q, кН/м
| P, кН
|
|
|
| 1,1
| 1,1
| 1,1
| 1,1
| 1,1
| 1,1
|
|
|
| 1,2
| 1,2
| 1,2
| 1,2
| 1,2
| 1,2
|
|
|
| 1,3
| 1,3
| 1,3
| 1,3
| 1,3
| 1,3
|
|
|
| 1,4
| 1,4
| 1,4
| 1,4
| 1,4
| 1,4
|
|
|
| 1,5
| 1,5
| 1,5
| 1,5
| 1,5
| 1,5
|
|
|
| 1,6
| 1,6
| 1,6
| 1,6
| 1,6
| 1,6
|
|
|
| 1,7
| 1,7
| 1,7
| 1,7
| 1,7
| 1,7
|
|
|
| 1,8
| 1,8
| 1,8
| 1,8
| 1,8
| 1,8
|
|
|
| 1,9
| 1,9
| 1,9
| 1,9
| 1,9
| 1,9
|
|
|
| 2,0
| 2,0
| 2,0
| 2,0
| 2,0
| 2,0
|
|
| е
| а
| б
| в
| г
| д
| е
|
Пример 6.Для рамы (рис. 6, а) требуется написать выражения для продольных сил N, поперечных сил Q и изгибающих моментов M на каждом участке в общем виде, построить эпюры N, Q, M и подобрать двутавровое сечение при R = 220МПа.
Решение.
1. Покажем и определим реакции опор (рис. 6, б):
 ;
;  ;
; 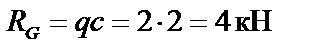 ;
;
 ;
;  ;
;  ;
;
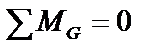 ;
;  ;
;  .
.
Проверка реакций опор:  ;
;  ;
;
 ;
;  ;
;
 .
.
Реакции опор найдены верно.
2. Определяем внутренние усилия N, Q, M на каждом участке
●Участок AB: z 1Î[0; 2];  ;
;  ;
;  ;
;  ;
;
 ;
;  ;
; 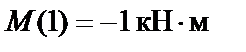 ;
;  .
.
●Участок BC: z 2Î[0; 3];  ;
;  ;
;
 ;
;  ;
; 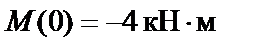 ;
;  ;
;
●Участок CD: z 3Î[0; 3];  ;
; 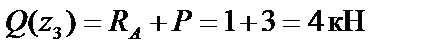 ;
;
 ;
;  ;
;
 ;
;  ;
;
●Участок FD: z 4Î[0; 2];  ;
;  ;
;  ;
;
●Участок GD: z 5Î[0; 2];  ;
;  ;
;
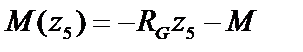 ;
; 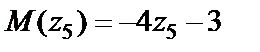 ;
;  ;
;  .
.
3. По вычисленным значениям строим эпюры N, Q, M (рис. 6, в).
| Эпюра изгибающих
моментов построена
на растянутом волокне
|
Проверка:
4. Подбор сечения. Ориентировочно подбираем номер двутавра из условия прочности при чистом изгибе, если R = 220 MПа:
 .
.
Принимаем двутавр №12, ГОСТ 8239–89,  ,
, 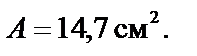
Проверка прочности двутавра №12 по нормальным напряжениям при совместном действии изгибающего момента и продольной силы:
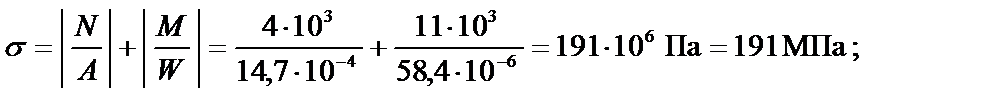
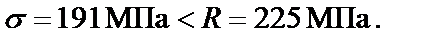
Условие прочности по нормальным напряжениям соблюдается.Двутавр № 12 принимаем окончательно.
Задача 7
ВНЕЦЕНТРЕННОЕ СЖАТИЕ СТЕРЖНЯ
Задание.Короткий стержень, поперечное сечение которого изображено на рис. 7, сжимается продольной силой Р, приложенной в заданной точке. Требуется: вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через Р и размеры сечения; найти допускаемую нагрузку Р при заданных размерах сечения и расчетных сопротивлениях материала на сжатие R c и на растяжение R р . Данные взять из табл. 7.
Таблица 7
| № строки
| № схемы
| a, см
| b, см
| № точки
| R c,МПа
| R р ,МПа
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| е
| д
| а
| б
| в
| г
|
Пример 7.Короткий стержень, поперечное сечение которого изображено на рис. 7, а, сжимается продольной силой Р, приложенной в точке 1. Требуется: вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении при а = 6 см; найти допускаемую нагрузку Р доп , если R с = 70 МПа, R р = 20 МПа.
Р е ш е н и е:
1. Находим площадь сечения:
 см2.
см2.
2. Определяем положение главных центральных осей. Сечение имеет две оси симметрии, следовательно, центр тяжести расположен в точке их пересечения, а сами оси симметрии являются главными осями. Направляем главные центральные оси x, y таким образом, чтобы точка приложения силы (т. 1) располагалась в первой координатной четверти.
3. Вычисляем главные центральные моменты инерции Ix и Iy:

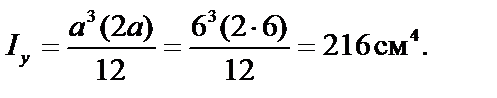
4. Находим квадраты радиусов инерции:

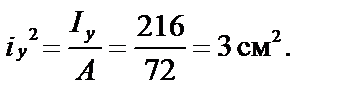
5. Определяем положение нейтральной (нулевой) линии (рис.7, б):

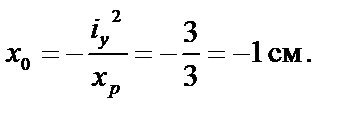
6. Вычисляем наибольшее растягивающее и наибольшее сжимающее напряжения. В сжатой зоне наиболее удаленной от нулевой линии является точка 1, а в растянутой – точка 2.
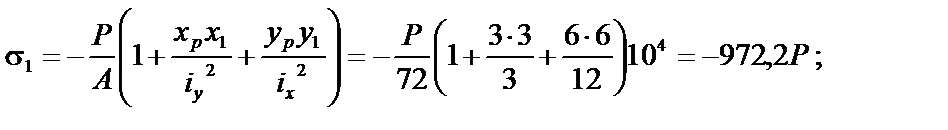
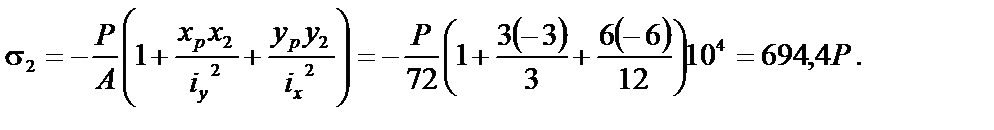
7. Определяемдопускаемую нагрузку:
●из условия прочности на растяжение 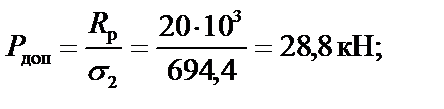
●из условия прочности на сжатие 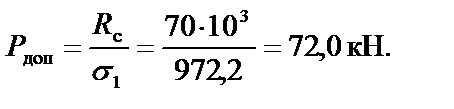
Окончательно за допускаемую нагрузку принимаем меньшее значение 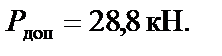
8. Построим эпюру напряжений от силы 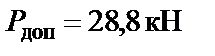 (рис.7, б):
(рис.7, б):

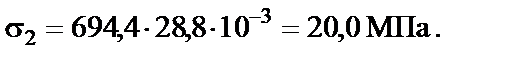
Задача 8
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Задание. На рис. 8 изображена в аксонометрии ось ломаного стержня круглого поперечного сечения, расположенная в горизонтальной плоскости, с прямыми углами в точках А и В. На стержень действует вертикальная нагрузка. Требуется: построить отдельно (в аксонометрии) эпюры изгибающих и крутящих моментов; установить опасное сечение и найти для него расчётный момент по III теории прочности.Данные взять из табл. 8.
 ;
;  ;
; 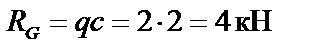 ;
; ;
;  ;
;  ;
;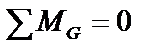 ;
;  ;
;  .
. ;
;  ;
; ;
;  ;
; .
. ;
;  ;
;  ;
;  ;
; ;
;  ;
; 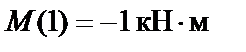 ;
;  .
. ;
;  ;
; ;
;  ;
; 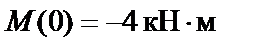 ;
;  ;
; ;
; 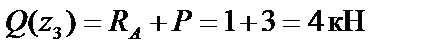 ;
; ;
;  ;
; ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
;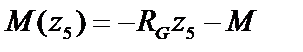 ;
; 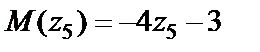 ;
;  ;
;  .
. ;
;
 ;
;
 .
.
 ;
;
 ;
;
 .
.
 .
. ,
, 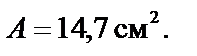
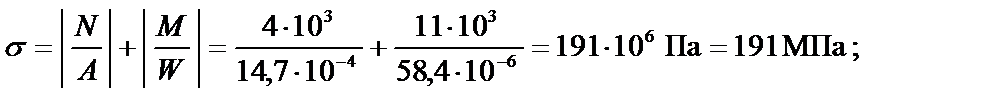
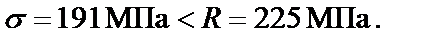
 см2.
см2.
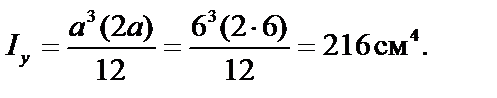

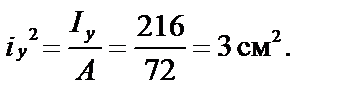

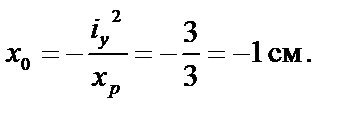
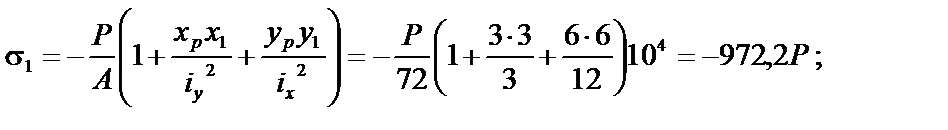
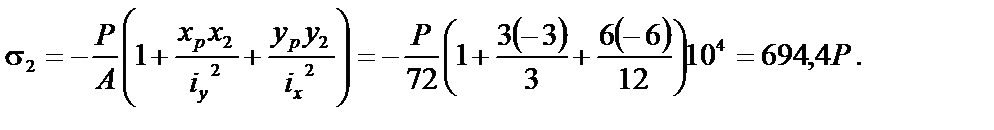
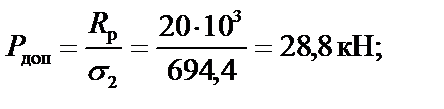
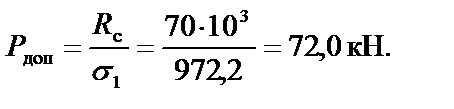
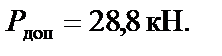
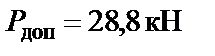 (рис.7, б):
(рис.7, б):