Краткие теоретические сведения. Большинство промышленных и даже бытовых электрических сетей – трехфазные, в которых отдельные фазы цепи электрически связаны между собой

Большинство промышленных и даже бытовых электрических сетей – трехфазные, в которых отдельные фазы цепи электрически связаны между собой. По разновидности этих связей схемы соединений могут быть “звезда” и “треугольник”.

Четырехпроводная трехфазная цепь при соединении “звездой” фазных обмоток генератора, и приемников представлена на рис. 1.5.1. Концы фазных обмоток генератора объединяют в одну точку 0 ′, называемой нейтральной точкой генератора. Соответственно концы приемников отдельных фаз объединяют в точку 0’, называемую нейтральной точкой приемников. Трехфазный генератор соединяют с нагрузкой четырьмя проводами.

 

ГЕНЕРАТОР ПОТРЕБИТЕЛИ

I_A

A^/ A

E_A’O’ U_A

Z_A

O^/ I_O Uл O

E_C’O’

E_B’O’ Z_C Z_B

C^/ B^/ C U_C B

U_B

U_BC I_B

I_C

 

Рис. 1.5.1. Электрическая схема трехфазной цепи “звезда” с нулевым проводом.

 

Провод, соединяющий нейтральные точки генератора и нагрузки называется нулевым, остальные провода – линейными. Напряжения и токи, имеющие место в фазных обмотках генератора или нагрузки, называют фазными. Токи в линейных проводах и напряжения между ними называют линейными. Исходя из структуры схемы “звезда” I _Л = I _Ф .

Комплексные сопротивления приемников в показательной форме можно представить в виде:

; ;

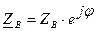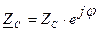
Приемники, имеющие одинаковые по модулю (Z_A = Z_B = Z_C = Z) и по характеру (j_A = j_B = j_C = j) сопротивления, создают для генератора и между собой так называемую симметричную нагрузку. Условие симметричности нагрузки:

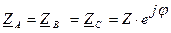
Нагрузка, распределенная между фазами одинаково по величине (Z_a = Z_b = Z_c) называется равномерной. Нагрузка в фазах одинаковой по характеру (j_a = j_b = j_c) называется однородной.

Для анализа режимов работы потребителей и электрической цепи в целом, по результатам расчета (измерений) ее параметров, строится векторная диаграмма напряжений и токов на потребителях. При этом, для практических целей, потерями напряжений в линии электропередачи пренебрегают, в виду их малости (не более 5%), т.е. поэтому для четырёхпроводной цепи: 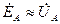; ; 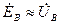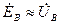. Для сложных цепей однофазного тока, а также для трехфазных цепей удобнее пользоваться, так называемыми, топографическими векторными диаграммами, в которых устанавливается однозначное соответствие между одноименными точками электрической цепи и векторной диаграммой. Обычно векторная диаграмма строится в следующей последовательности: .

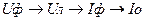Известно, что вектора фазных напряжений имеют одинаковую амплитуду, частоту и сдвинуты по фазе на угол 120°: ; ; .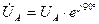

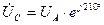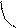
A Построим их в заданном масштабе.

U­_A U_AB M_U … ;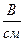

I_A Вектора линейных напряжений

j_A определим по уравнениям,

U_CA составленным по второму закону

Кирхгофа

O ; ;

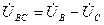I_O U_B

I_C j_C

C

 

U_C U_BC B

 

Рис. 1.5.2. Векторная диаграмма для схемы “звезда” с нулевым проводом.

 

Из рассмотрения треугольников напряжений, выраженных уравнениями Кирхгофа, следует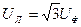

Симметрия и стабильность линейных напряжений электрической цепи обеспечивается источниками электрической энергии и является гарантией нормальной работы цепи и потребителей.(Постоянство уровня напряжения является также важнейшей характеристикой качества электрической энергии).

Положение векторов тока зависит от величины и характера нагрузки в фазах. Примем, следующие нагрузки:

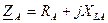- активно-индуктивная, j_A>0. 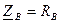- активная, j_В=0. 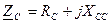- активно-емкосная, j_С <0. При этом пусть Z_A> Z_B> Z_C. Тогда ; ; .

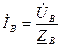Построим эти вектора в принятом масштабе ;

(Если векторная диаграмма строится вне координатной сетки, то положение векторов тока относительно одноименных векторов фазных напряжений определяется углами j_Фi = arctg 0,т.к. j_i= j_ui-j_ii (рис. 1.5.2.)

Ток нулевого провода определяется в виде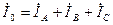

Для случая симметричной нагрузки, когда , I_A=I_B=I_C ,а I₀=0. И необходимость в нулевом проводе отпадает. Таким образом нулевой провод выравнивает потенциалы нейтральных точек О’,О. при несимметричной нагрузке. фаз. Использование трехпроводной звезды дает значительный экономический эффект,за счет экономии материала проводов.Однако,в случае несимметричной нагрузки режимы работы потребителей, по напряжению, изменяются. Действительно, при изменении сопротивления одной фазы,очевидно,изменяется ток этой фазы, а с учетом первого закона Кирхгофа 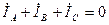, изменяются токи и других фаз, что возможно только при изменении фазных напряжений: 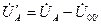; ; 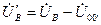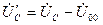, где 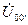- разность потенциалов между нейтральными точками генератора и потребителей, определяется в виде:

; (a), где 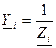- комплекс полной проводимости i – ой фазы.

Топографическая векторная диаграмма для трехпроводной “звезда” строится аналогично и в тех же масштабах, что и рис 1.5.2. Сначала строится векторная диаграмма напряжений (ЭДС) источника. Относительно точки О¹ определяем положение точке О(а). Затем откладываем вектора фазных напряжений 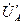, , 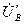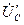. Вектора линейных напряжений источника и потребителей остаются неизменные. Вектора токов откладываем относительно одноименных векторов напряжений 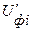под углом 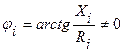. Для принятых нагрузок векторная диаграмма для трехпроводной звезды представлена на рис. 1.5.3 M_U 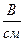; M_I …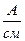

 

A

 

U_AB

U’_A E_A»U_A

 

j_A I_A

U_CA O’

E_C­ »U_C U_00’ E_B­ »U_B

I_C j_C U’_C O I_B

U_BC U’_B

C B

 

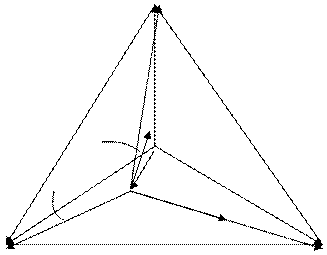
Рис. 1.5.3. Векторная диаграмма для трехпроводной “звезды”.

 

Из векторной диаграммы следует, что потребители фаз А и В работают в режиме перенапряжения U_A’>U_A; U_B’>U_B, а потребители фазы С находятся в режиме пониженного напряжения. Естественно, что нарушение режимов работы по напряжению существенно снижает технико-экономические показатели потребителей.

Таким образом явление переноса фазных напряжений в трехпроводной “звезде” очень нежелательно и даже опасно. Трехпроводная “звезда” может использоваться только для симметричной нагрузки. Во избежание бесконтрольного перехода от четырехпроводной к трехпроводной “звезде”, при несимметричной нагрузке, (что чаще всего бывает) плавкие предохранители и другие виды защиты в нулевой провод не ставят.

 

Порядок выполнения работы

 

1. Собрать схему рис. 1.5.4.

2. Определить характер нагрузки в фазах цепи (рис. 1.5.4).

3. Включить нагрузку любых двух фаз с помощью ключей К_i. Нагрузку третьей фазы изменять последовательно от холостого хода до максимальной (включены оба ключа). Для всех трех режимов записать параметры, указанные в табл. 1.5.1

ПРИМЕЧАНИЕ:

1). Параметры нагрузочных резисторов имеют разброс в пределах ±5% от номинала.

2.) Все измерительные приборы имеют погрешность прибора согласно его класса точности, а также погрешность измерений.

3.) Результаты измерений необходимо фиксировать с учетом указанных допусков, т.е. фиксировать различие результатов измерений только превышающие их погрешности, а также заведомо известные малые измерения отдельных параметров, например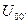

4. По данным табл. 1.5.1 построить (в масштабах, позволяющих различать все вектора), совмещенные топографические диаграммы напряжений и токов, для четырехпроводной “звезды”.

5. Тумблером К₇ разомкнуть нулевой провод. Изменяя нагрузку одной фазы аналогично п.3 снять измерения согласно табл. 1.5.2.

6. По данным табл. 1.5.2 построить топографическую диаграмму аналогично п.4 для трехпроводной “звезды” в тех же масштабах.

 

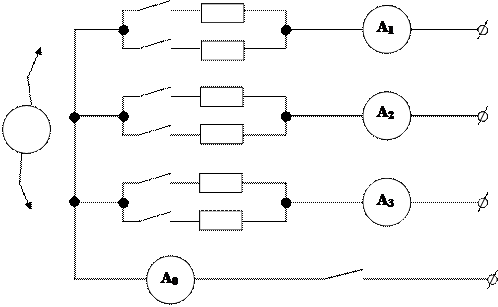K₁ R

 

K₂ A

 

K₃ R

 

V

K₄ B

 

K₅ R

 

 

C

 

K₆ K₇

O

 

Рис. 1.5.4. Электрическая схема лабораторной установки.

 

 

Таблица 1.5.1

измеряем. величина режим работы потреб	IA [A]	IB [A]	IC [A]	IN [A]	UaO [B]	UbO’ [B]	UcO’ [B]	UAB [B]	UBC [B]	UCA [B]
холостой ход фазы
неравномерная нагрузка
симметричная нагрузка

 

 

` Таблица 1.5.2

измер.ве личина режим работы потреб	IA [A]	IB [A]	IC [A]	IO [A]	UAO’ [B]	UBO’ [B]	UCO’ [B]	UAB [B]	UBC [B]	UCA [B]	UOO’ [B]
холостой ход фазы
неравномерная нагрузка
симметричная нагрузка

 

 

Контрольные вопросы

 

1. Какие напряжения называются фазными, линейными напряжениями?

2. Покажите, что I _Л = I _Ф ; 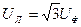при соединении приемников звездой. В каких случаях эти соотношения справедливы?

3. Когда применяются схемы звезды с нулевым проводом и без него?

4. Как изменяется режим работы потребителей в трехпроводной “звезде” при несимметричной нагрузке?

5. Почему не ставят плавкий предохранитель в нулевой провод?

6. Как влияет на фазные напряжения изменение нагрузки одной фазы?

7. Как определить величину и фазу тока в нулевом проводе?

 

ЛИТЕРАТУРА: [1,3].

 

РАБОТА N 1.6. ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ С СОЕДИНЕНИЕМ

ПОТРЕБИТЕЛЕЙ ПО СХЕМЕ ТРЕУГОЛЬНИК”.

 

Цель работы:

Анализ режимов работы потребителей в трехфазной цепи,соедененныч по схеме “треугольник”.