В цепи постоянного тока все проводники и потребители обладают электрическим сопротивлением, которое принято называть омическим. В цепях переменного тока имеют место следующие виды сопротивлений: активное– Rr; реактивное – X (индуктивное – XL, емкостное – XC) и полное – Z. Указанные сопротивления связаны между собой соотношениями, полученными из треугольника сопротивлений – рис. 1.1.1.
R = Zcosj; X =Zsinj;
j X Z = 
; j =arctg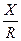 
 |
R
Рис. 1.1.1 Треугольник сопротивлений.
Активным сопротивлением обладают элементы, в которых электрическая энергия необратимо преобразуется в тепловую, световую, механическую и т.д. (резисторы, лампы накаливания, электронагревательные приборы и др.). Реактивным сопротивлением обладают элементы, способные запасать энергию в магнитном или электрическом полях, например, катушки индуктивности и конденсаторы. По своей физической природе реактивное сопротивление отличается от активного, и оно обусловлено влиянием магнитного и электрического полей, связанных с цепью.
При постоянном токе магнитный поток, создаваемый катушкой индуктивности, в установившемся режиме постоянен, сопротивление катушки невелико, так как обусловлено только омическим сопротивлением медного провода обмотки. При переменном токе магнитный поток в катушке изменяется во времени по закону sin и согласно закону электромагнитной индукции, индуктирует э.д.c. самоиндукции такого направления, которое препятствует изменению тока.Э.д.с. самоиндукции катушки индуктивности оказывает противодействие переменному току, характеризующееся величиной индуктивного сопротивления: XL = wL, где w = 2pf - угловая частота переменного тока; L - индуктивность.
При постоянном токе и постоянном значении, приложенного напряжения, заряд конденсатора q=CU, гдеС – емкость конденсатора, сопротивление конденсатора бесконечно велико за счет прослойки диэлектрика между его обкладками. Поэтому конденсатор постоянный ток “не пропускает”. Переменное напряжение создает изменяющийся во времени заряд и в цепи возникает ток, величина которого зависит от величины емкости С конденсатора. Противодействие конденсатора переменному току характеризуется емкостным сопротивлением
В отличие от активного, индуктивное и емкостное сопротивления не связаны с необратимым преобразованием электрической энергии в энергию другого вида, за что получили название реактивных. В общем случае, когда ветвь содержит последовательно соединенные индуктивность и емкость, оно равно разности индуктивного и емкостного сопротивлений:
Знак реактивного сопротивления определяется тем какое из сопротивлений преобладает. При XL>XC величина X положительна, при XL <XC - отрицательна.
При заданном напряжении действующее значение тока определяется формулой:
, выражающей закон Ома для пассивной ветви цепи переменного тока.
Энергетические процессы в цепях переменного тока имеют особенности по сравнению с цепями постоянного тока. Помимо необратимого преобразования электрической энергии в энергию другого вида в них наблюдается процесс обратимого преобразования электрической энергии. При возрастании тока (а следовательно и магнитного потока) электрическая энергия поступает к потребителю, преобразуется и накапливается в нем в виде энергии магнитного поля. Энергия магнитного поля достигает максимума при максимальном значении тока. При убывании тока энергия магнитного поля преобразуется в электрическую энергию и возвращается в цепь. Происходит гармонический обмен энергией между магнитным полем индуктивности и цепью.
Подобное преобразование электрической энергии в энергию электрического поля наблюдается и в емкости при приложенном синусоидальном напряжении. При возрастании напряжения конденсатор потребляет энергию из цепи, запасая ее в электрическом поле (заряжается), при убывании напряжения отдает энергию обратно в цепь (разряжается).
При анализе энергетических процессов в цепях переменного тока используются четыре понятия мощности.
1. Мгновенная мощность: р = u i, где 
, 
- мгновенные значения напряжения и тока, изменяющиеся во времени по синусоидальному закону. Мгновенная мощность дает значение мощности, потребляемой ветвями цепи в произвольный момент времени.
2. Активная мощность: P=UIcosj=I2R, где 
и 
- действующее значения напряжения и тока; j=yu -yi - сдвиг по фазе между током и напряжением; cosj -коэффициент мощности. Активной мощностью оценивается как средняя за период скорость необратимого преобразования электрической энергии в энергию другого вида. По активной мощности ведут расчет теплоэнергетических характеристик потребителей. Активная мощность измеряется в ваттах (Вт).
3. Реактивная мощность Q=UIsinj=I2X. Понятие реактивной мощности, применяемое для оценки процесса обмена энергией между электрическим и магнитным полями ветвей цепи и источником, измеряется в вольтамперах реактивных (ВАр).
4. Полная мощность S=UI=I2Z. Полной мощностью называют расчетную величину, характеризующую пропускную способность цепи, и она характеризует предельную величину полезно используемой мощности потребителей. Измеряется в вольтамперах (ВА).
Коэффициент мощности cosj показывает, в какой степени используется пропускная способность ветви.
Составляющие мощности ветви (цепи) связаны соотношениями прямоугольного треугольника (рис. 1.1.2) подобного треугольнику сопротивлений. Из треугольника мощностей следуют соотношения: P=cosj, Q=Ssinj, S= 
, 
. Значение активной, реактивной, полной мощностей и параметров участка цепи могут быть экспериментально определены с помощью ваттметра, амперметра и вольтметра, включенных по схеме(рис.1.1.3.).
 |
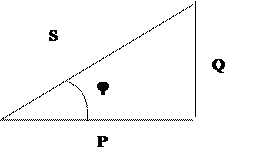Рис. 1.1.2. Треугольник мощностей.
Рис. 1.1.3. Схема подключения измерительных приборов в электрической цепи переменного тока.
Ваттметр измеряет активную мощность Р, амперметр и вольтметр показывают действующие значения тока и напряжения. Используя показания приборов, рассчитываем значения величин по формулам:
cosj = 
, j =arccos , Z= 
, 
, X = Zsin 
, S = UI, Q = UIsinj.
Результаты всех измерений получаются с погрешностями, поэтому результаты, полученные косвенным путем, не должны противоречить физическому смыслу.(Например: cos j > 1, Z < R и т.д.).
Анализ цепей переменного тока, сопровождается построением векторной диаграммы. Векторная диаграмма это совокупность взаимосвязанных одноименных векторов, изображающих синусоидально изменяющиеся во времени токи и напряжения цепи. При построении векторной диаграммы, длины векторов берут равными(в принятых масштабах) действующим значениям величин; углы между ними – соответствующим сдвигам фаз.
Реальная катушка индуктивности представляет собой нагрузку активно-индуктивного характера, так как вследствие потерь мощности на нагрев провода обмотки, она обладает помимо индуктивного сопротивления XL, активным сопротивлением RL. Реактивное сопротивление катушки равно: X = XL, сдвиг по фазе между током и напряжением: 
,что означает, что ток отстает по фазе от напряжения (вектор напряжения на диаграмме повернут относительно вектора тока против часовой стрелки).
B реальном конденсаторе, при низких частотах 
Гц, практически отсутствуют потери мощности, его можно рассматривать как емкостную нагрузку. Реактивное сопротивление конденсатора X=Xc, cдвиг по фазе между током и напряжением:
°, что означает, что ток опережает по фазе напряжение на 90° (вектор напряжения повернут относительно вектора тока по часовой стрелке).
На рис. 1.1.4 представлена, содержащая последовательно соединенные резистор и катушку. На рис.1.1.5 – качественная векторная диаграмма этой цепи. MI =…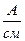 
; MU = …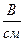 
|
U1 I
Рис. 1.1.4.Электрическая цепь. Рис. 1.1.5. Векторная диаграмма.
При последовательном соединении элементов построение диаграммы начинают с вектора тока, так как ток на всех участках цепи один и тот же. Затем, в принятом масштабе, строят вектора напряжений 
на участках с резистором и катушкой, используя известные значения углов j для этих участков(j1 =0, 0< j2 < 
).Напряжение источника, в соответствии со вторым законом Кирхгофа, должно удовлетворять условию: 
Положение точки “ b ”, а, следовательно, и положение векторов определяется способом засечек. Угол j - сдвиг по фазе между напряжением U и током I на входе цепи.
Аналогично строится диаграмма для цепи, содержащей последовательно соединенные резистор и конденсатор.
Порядок выполнения работы.
1. Собрать схему рис. 1.1.6.
2. Поставив тумблер К в положение 1, измерить значение тока, напряжения и активной мощности на отдельных участках и для цепи в целом.
3. Переключить тумблер К в положение 2 и повторить те же измерения.
4. Результаты измерений занести в табл. Вычислить значения величин, указанных в табл.
5. Для цепей, соответствующих двум положениям тумблера К, построить в одинаковых масштабах векторные диаграммы.
 |
Рис. 1.1.6. Схема лабораторной установки.
Таблица
| N це пи | участок электрической цепи: | измерено | Вычислено | |||||||||
| I [A] | U [B] | P [Bт] | cosj | j гр | Z [Oм] | R [Oм] | X [Oм] | Q [ВАp | S [ВА] | |||
| с резистором | ||||||||||||
| с катушкой индуктивности | ||||||||||||
| вся цепь | ||||||||||||
| с резистором | ||||||||||||
| С конденсатором | ||||||||||||
| вся цепь |
Контрольные вопросы.
1. Назовите параметры характеризующие пассивный участок цепи переменного тока.
2. Объясните наличие у катушки индуктивности активного сопротивления. Объясните физический смысл индуктивного сопротивления.
3. Объясните особенности энергетических процессов в цепях переменного тока.
4. Чем отличаются реальные элементы L и C от “ идеальных”.
5. Назовите четыре понятия мощности, применяемые при анализе энергетических процессов в цепях переменного тока.
6. Как экспериментально могут быть определены параметры участка цепи?
7. Объясните порядок построения векторных диаграмм для цепей с последовательным соединением элементов.
8. В каких единицах измеряются составляющие мощности?
ЛИТЕРАТУРА /1,2/.
РАБОТА N 1.2. ИССЛЕДОВАНИЕ НЕРАЗВЕТВЛЕННОЙ ЦЕПИ ПЕРЕМЕННОГО
