3.1. Классический метод расчета.
Порядок расчета классическим методом был описан в пп.2.1.
3.1.1. Послекоммутационная схема (рис. 4) и уравнения Кирхгофа (1) практически не изменяются по сравнению с п.2.1.
Единственным исключением является появление синусоидальных источников e 1(t), J (t) вместо постоянных источников.
Узел : 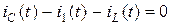
Узел ‚: 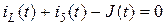
Узел ƒ: 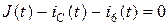 (8)
(8)
Контур I: 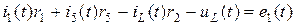
Контур II: 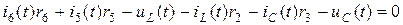
3.1.2. Характеристическое уравнение и его корни зависят только от конфигурации цепи после коммутации и ее пассивных параметров, то есть остаются неизменными по сравнению с п.2
3.1.3. Не изменяется и общий вид решения
3.1.4. Установившееся значение iLуст (t) и uCуст (t) будут синусоидальными функциями времени, так как источники схемы e 1(t) и J (t) – синусоидальны.
Расчет установившегося режима в схеме после коммутации будем проводить комплексным методом так как установившийся режим – синусоидальный. Комплексная схема после коммутации приведена на рис. 15.
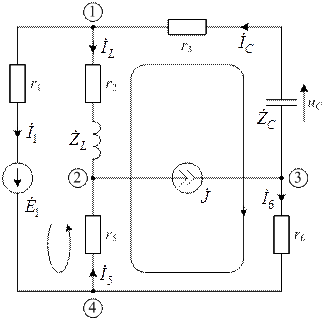
|
| рис. 15 |
В схеме рис. 15
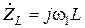 ,
, 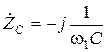 ,
, 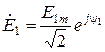 ,
, 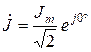
, 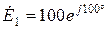 ,
, 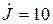 ,
, 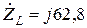 ,
, 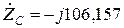
Уравнение Кирхгофа в комплексной форме для схемы рис. 15 имеют вид:
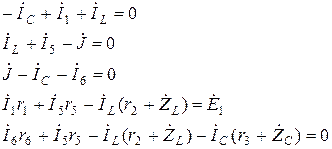
В матричной форме:
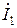
| 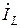
| 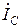
| 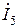
| 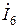
|
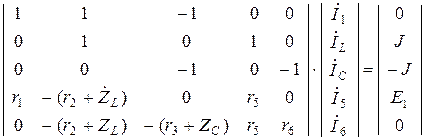
Результаты расчета в системе MathCAD приведены ниже
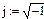
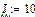
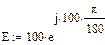
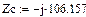
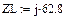
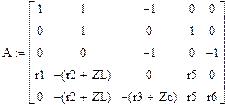
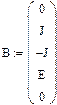
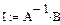
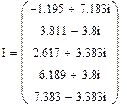
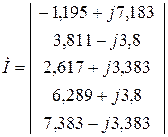
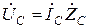
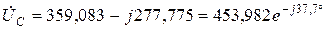
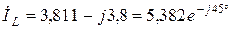
Представление iLуст (t) и uCуст (t) в виде суммы синусоиды и косинусоиды удобно при сравнении этих значений в операторном методе.
3.1.5. При расчете ННУ необходимо рассчитать докоммутационный установившийся синусоидальный режим в комплексной схеме до коммутации (рис.16)
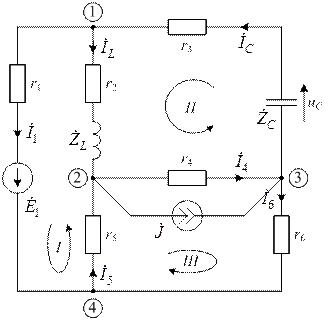
|
| рис. 16 |
Уравнения Кирхгофа для этой схемы имеют вид:
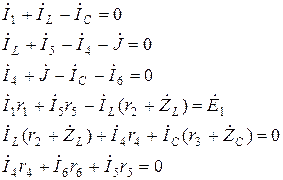
В матричной форме
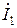
| 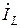
| 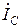
| 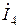
| 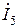
| 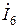
|
Результаты расчета в системе MathCAD приведены ниже
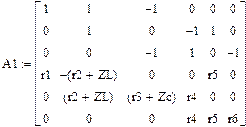
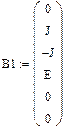
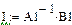
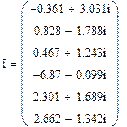
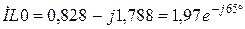 ,
, 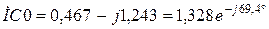
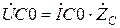
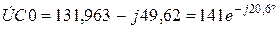
В результате расчета докоммутационного установившегося синусоидального режима получим:
→
→
Следовательно ННУ для схемы при синусоидальных источниках
3.1.6. При определении ЗНУ можно использовать уравнения из п.2.6.
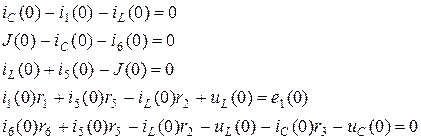
В этих уравнениях уже известны, что следует из законов коммутации. Значение J (0) и e 1(0) находятся из аналитических выражений этих синусоидальных источников, записанных при
,
Решение в системе MathCAD дает:
| i 1(0) | iC (0) | i 5(0) | i 6(0) | uL (0) |
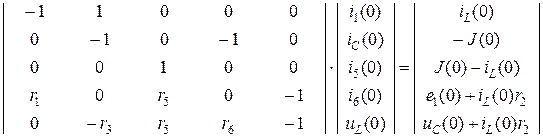
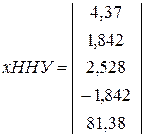
Следовательно
Тогда
3.1.7. Постоянные интегрирования A 1, A 2, B 1, B 2 находятся по найденным ННУ, ЗНУ и iLуст (0), uCуст (0).
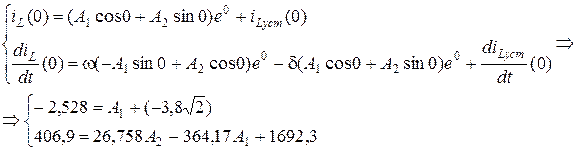
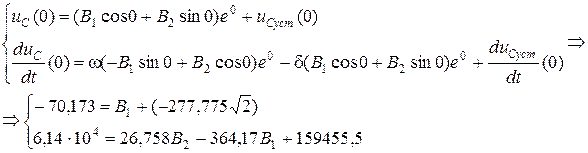
В представленных системах уравнений
,
что следует из выражений
записанных при
Решение записанных систем дает:
,
,
3.1.8. Окончательные выражения для iL (t) и uC (t)
3.1.9. Ток в ветви без реактивных элементов
Графики рассчитанных iL (t), uC (t), i 5(t) классическим методом приведены на рис. 17, 18.
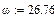
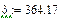
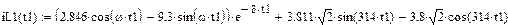
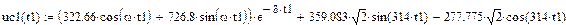
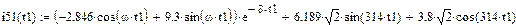
рис.17
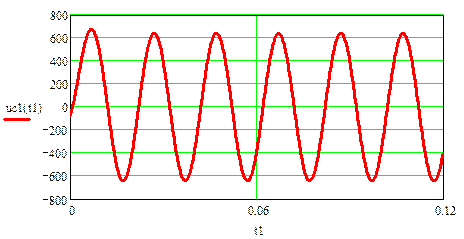
рис.18
3.2. Операторный метод расчета переходного процесса в цепи с синусоидальными источниками.
Операторная послекоммутационная схема не изменится по сравнению с п.2.2
Изображения синусоидальных источников e 1(t) и J (t) по Лапласу имеют вид:
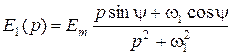 ,
,
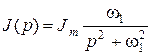
С учетом исходных данных цепи
Числовые значения дополнительных источников операторной схемы
Уравнения для операторных контурных токов по аналогии с п.2.2 принимают вид, с учетом:
После подстановки числовых значений исходных данных:
Используя решающий блок GIVEN…FIND системы MathCAD, получим
Корни
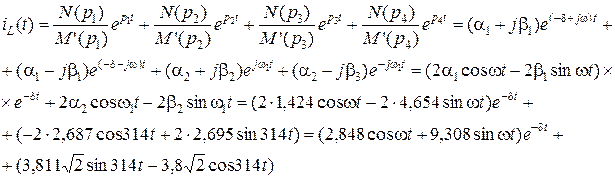
Результаты расчета классическим и операторным методами совпадают.
3.3. Расчет переходного процесса при синусоидальных источниках численными методами.
3.3.1. Явный метод Рунге-Кутта 4ого порядка
Воспользуемся стандартной процедурой системы MathCAD rkfixed(X,TO,Tmax,N,d) как и в случае, представленном в п.2.3.1. Система дифференциальных уравнений в нормальной форме Коши остается неизменной, как и в п.2.3.1, за исключением источников схемы. Вместо постоянных источников e 1 и J необходимо использовать синусоидальные источники, являющиеся функциями времени
,
.
Таким образом, получим
где
Постоянные a 1, b 1, a 2, b 2 остаются неизменными, как и в п.2.3.1. В качестве начальных условий взяты значения, рассчитанные ранее (п.3.1)
,,
Графики iL (t) и uC (t) приведены на рис. 19
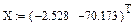
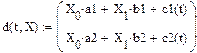

Ток в индуктивности
 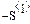
| Напряжение на емкости
 
|
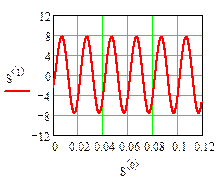
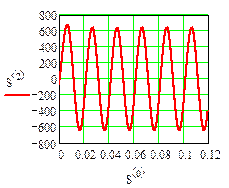
рис.19
Длительность переходного процесса Tmax можно оценить по значению вещественной части корня характеристического.
Тогда
3.3.2. Метод дискретных резистивных схем
Расчет переходного процесса численным методом на основе дискретной схемы при синусоидальных источниках e 1(t) и J (t) практически не отличается от аналогичного расчета при постоянных источниках (п. 2.3.2)
В качестве начальных значений неизвестных i 1(0), iL (0), iC (0), i 5(0), i 6(0), uC (0) необходимо взять рассчитанные ННУ и ЗНУ из пп. 3.1.5, 3.1.6.
,
,
,
,
,
,
Начальные значение дополнительных источников
,
,
,,
Δ t – выбирается в пределах 10-4 – 10-6 сек.
Начальные значения синусоидальных источников
,
Начальное значение тока



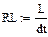
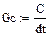
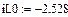
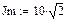
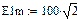


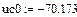
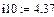
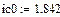
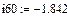
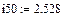

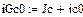

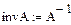
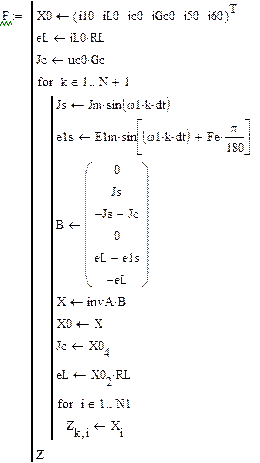




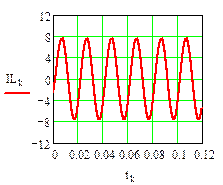
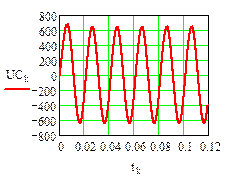
рис.20
Результаты расчета аналитическими методами (классическим и операторным) и численными методами (Рунге-Кутта и с помощью дискретной схемы) совпадают (рис. 17, 18, 19, 20).




