Расчет переходных процессов в электрических цепях.
Постановка задачи
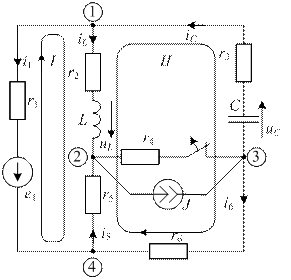
1.1. Выполнение задания по расчету переходных процессов следует начинать с выбора схем и исходных данных к ним по коду варианта: KLMNP.QRST.
|
| рис. 1 |
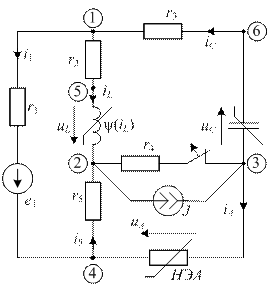
По коду варианта (например, для кода II1234.0111) вычертить две схемы: для линейной и нелинейной цепей.
На рис. 1 приведен граф цепи, соответствующий коду варианта.
На рис. 2 приведена схема линейной цепи.
На рис. 3 приведена схема нелинейной цепи.
Параметры линейной цепи в соответствии с кодом варианта:
а) для цепи с постоянными источниками:
б) для цепи с синусоидальными источниками:
| 
|
| рис. 2 | рис. 3 |
Параметры нелинейной цепи в соответствии с кодом варианта:
а) для цепи с постоянными источниками:
Вольт-амперная характеристика (ВАХ) НЭА
| uA, В | ||||||||
| iA, А | 0,3 | 0,5 |
Вебер-амперная характеристика (ВАХ) нелинейной индуктивности
| ψ, Вб | 0,126 | 0,18 | 0,204 | 0,24 | 0,264 | 0,278 | 0,288 | 0,3 | |
| iL, А | 0,2 | 0,3 | 0,5 |
Кулон-вольтная характеристика (КВХ) нелинейной емкости
| q ·103, Кл | 0,6 | 0,94 | 1,34 | 1,64 | 1,82 | 1,92 | ||
| uC, В |
б) для схемы с синусоидальными источниками:
Вольт-амперная характеристика (ВАХ) НЭА
| uA, В | ||||||||
| iA, А | 0,3 | 0,5 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 |
Вебер-амперная характеристика (ВАХ) нелинейной индуктивности
| ψ, Вб | 0,126 | 0,18 | 0,204 | 0,24 | 0,264 | 0,278 | 0,288 | 0,3 | |
| iL, А | 0,2 | 0,3 | 0,5 | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 |
Кулон-вольтная характеристика (КВХ) нелинейной емкости
| q ·103, Кл | 0,6 | 0,94 | 1,34 | 1,64 | 1,82 | 1,92 | 2,0 | |
| uC, В |
1.2. Уравнения Кирхгофа для линейной цепи после коммутации (рис. 2)
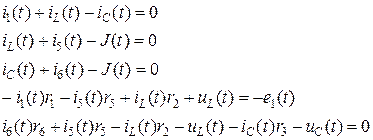
Уравнения связи:
; 
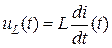В качестве неизвестных выступают: i 1(t), iL (t), iC (t), i 5(t), i 6(t)
1.3. Уравнения гибридного метода для нелинейной цепи после коммутации (рис. 3). Гибридные уравнения получаются из уравнений Кирхгофа, в которых уравнения для независимых контуров разбиваются на части. Каждая часть устанавливает связь между потенциалами узлов схемы, включая и простые узлы (на рис. 3 узлы … и † – простые узлы), и токами в ветвях. Таким образом в системе гибридных уравнений в качестве неизвестных выступают не только токи в ветвях, но и потенциалы всех узлов цепи (в том числе и простых узлов). Такое усложнение (увеличение числа неизвестных оказывается оправданным при расчетах нелинейных цепей, или реализации итерационных (численных) методов расчета.
Для схемы рис. 3 гибридные уравнения принимают вид:
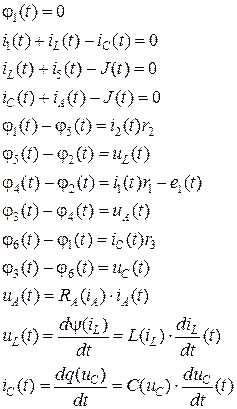
В гибридных уравнениях в качестве неизвестных выступают:
i 1(t), iL (t), iC (t), i 5(t), iA (t), φ2(t), φ3(t), φ4(t), φ5(t), φ6(t), uC (t), uA (t), uL (t).
Расчет переходных процессов в линейной цепи постоянного тока.
Для линейной цепи (рис. 2) необходимо рассчитать по заданию ток в индуктивности L, напряжение на емкости C и ток в ветви, не содержащей реактивных элементов в схеме после коммутации. Расчет должен быть произведен классическим и операторным методами.
Классический метод
Расчет переходного процесса классическим методом можно проводить по нижеследующему алгоритму:
1. Нарисовать схему после коммутации (рис. 4), указать на ней направления токов в ветвях и составить систему уравнений Кирхгофа для мгновенных значений токов и напряжений. Как известно, после коммутации в цепи токи и напряжения изменяются во времени.
|
| рис. 4 |
В схеме рис. 4 три независимых узла , ‚ и ƒ, пять неизвестных токов в ветвях i 1, i 2, iС, i 5, i 6, поэтому необходимо составить 5 уравнений Кирхгофа: из них по 1 закону Кирхгофа три уравнения, по 2 закону Кирхгофа () два уравнения (– число неизвестных токов в схеме.
Уравнения Кирхгофа для схемы рис. 4:
(1)
2. Составить выражение для характеристического уравнения и найти его корни.
Как известно из теории, в линейной электрической цепи количество реактивных элементов схемы определяет порядок дифференциального уравнения для расчета переходного процесса (для «корректных» задач).
Следовательно, для данной цепи дифференциальное уравнение будет 2 порядка. Решение его определяется видом корней характеристического уравнения. Характеристическое уравнение может быть получено одним из трех способов.
Способ первый:
Свести систему уравнений Кирхгофа (1) к одному уравнению с одним неизвестным. В качестве такого неизвестного можно брать любой из трех токов или любое напряжение в схеме после коммутации. При этом следует учесть, что ;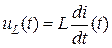 
. В данном случае сведение системы пяти уравнений к уравнению с одним неизвестным представляется нецелесообразным из-за громоздкости решения.
Данный способ можно использовать для схем, описываемым одним или двумя уравнениями Кирхгофа.
Способ второй – матричный:
При таком способе исходная система уравнений Кирхгофа (1) записывается только для свободных составляющих переходных токов и напряжений, что соответствует свободному режиму, то есть режиму, когда источники схемы после коммутации исключаются из схемы (гасятся). В системе (1) при этом правая часть будет нулевая.
или с учетом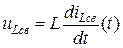 
, 
(4)
Из системы (4) составляется матрица коэффициентов при токах i 5 св , i 6 св , i 1 св , iLсв, iCсв. При этом учитывают, что коэффициентом при токе входящем в производную, является p 
, а коэффициентом при токе под интегралом является 
. Тогда матрица коэффициентов имеет вид
Определитель этой матрицы, приравненный к нулю и является характеристическим уравнением. Раскрыть определитель с рангом, равным 5 также является трудоемкой задачей. Данный способ можно использовать при получении характеристического уравнения в схемах с количеством уравнений Кирхгофа, не превышающих трех.
Способ третий:
Составляется выражение для входного комплексного сопротивления схемы после коммутации при погашенных источниках относительно точек разрыва в любой ветви этой схемы (рис. 5).
|
| рис. 5 |
В этом выражении
, 
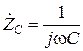
Далее сомножители j ω в комплексных сопротивлениях реактивных элементов заменяются на параметр «p» и полученное выражение приравнивается к нулю
(5)
Выражение (5) является характеристическим уравнением. После алгебраических преобразований
,
где,,,
Полученное выражение представим в ви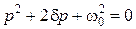де: 
, где
, 
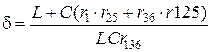Для конкретных числовых данных:
, 
Корни характеристического уравнения:
,
где – коэффициент затухания
– частота свободных колебаний
Корни характеристического уравнения комплексные сопряженные.
3. По виду корней характеристического уравнения записывается общий вид решения дифференциального уравнения.
Вид решения зависит от вида корней характеристического уравнения:
а) если корни вещественные
,
б) если корни комплексные
,
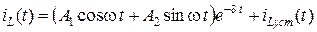Надо отметить, что если источники в схеме постоянные (не зависят от времени), то и значения токов и напряжений в установившемся режиме тоже будут постоянными
, 
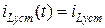4. Рассчитывается установившийся режим в схеме после коммутации.
Расчет установившегося режима в схеме после коммутации можно проводить по уравнениям Кирхгофа из п.1, записав их для момента времени.
В установившемся режиме постоянного тока:,. Тогда уравнения системы (1) примут вид
С учетом числовых значений исходных данных результаты расчета установившегося режима:
;;;.
5. Определяются независимые начальные условия (ННУ)
К ННУ, как известно, относятся токи в индуктивностях iL (0) и напряжения на емкостях uC (0).
Находятся эти ННУ в соответствии с законами коммутации:
,
Аргумент «0–» означает докоммутационный момент коммутации. Теоретически, считая коммутирующий ключ идеальным, этот момент совпадает с, практически же – это нулевой момент, предшествующий коммутации. Поэтому для расчета ННУ необходимо рассчитать установившийся режим в схеме до коммутации (рис. 6)
|
| рис. 6 |
В схеме рис. 6 был установившийся режим постоянного тока, поэтому ток в емкости был равен нулю (поэтому ветвь с емкостью изображена пунктиром), и напряжение на индуктивности тоже равно 0 (поэтому элемент индуктивности изображен в виде «закоротки»).
Следует внимательно следить за выбором стрелок тока iL (0–) и напряжения uC (0–) в схеме рис. 6. Направление этих стрелок в элементах L и C должно совпадать с направлением стрелок в схеме после коммутации (рис. 4).
Уравнения по законам Кирхгофа для схемы рис. 6 имеют вид:
Узел :,
Узел ƒ:,
Узел „:,
Контур I:,
Контур II:
Решение полученной системы с учетом числовых значений исходных данных и с учетом дает:
;;;;,
Для нахождения uC (0–) составляется уравнение по 2 закону Кирхгофа для контура , ‚, ƒ
→
С учетом числовых исходных данных ННУ:;.
6. Определяются зависимые начальные условия (ЗНУ).
Как известно, к ЗНУ относятся все остальные токи, напряжения и их производные по времени в схеме после коммутации, записанные для момента коммутации. Среди множества ЗНУ данной цепи нас будут интересовать только значения 
и 
, то есть ЗНУ именно для тех неизвестных, решение которых ищется по условию задания.
Для их определения следует систему уравнений (1) из п.1 записать для момента времени и решить ее. При этом необходимо использовать результаты расчета ННУ п. 5.
(5)
В этой алгебраической системе (5) уже известны (из п. 5)
,
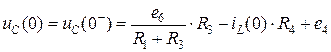
С учетом числовых исходных данных решение системы (5) дает следующие результаты:
;
;
;
;
.
Значения производных и можно найти из известных уравнений связи тока и напряжения на реактивных элементах L и C.
, 
,
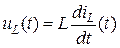откуда
, 
.
Численные значения ЗНУ равны:
, 
7. Находятся постоянные интегрирования (A 1, A 2, B 1, B 2)
Постоянные интегрирования дифференциальных уравнений для тока iL (t) и напряжения uC (t) можно найти, используя начальные условия (ННУ и ЗНУ)
Для этого общий вид решения из п. 3 и его производную по времени следует записать при:
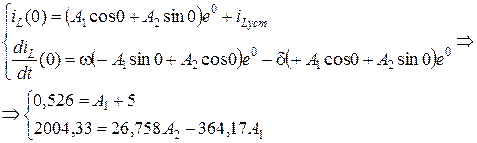
Решение этих уравнений дает
| A 1 = –4,474 | B 1 = –474,2 |
| A 2 = 14 | B 2 = –1103,3 |
8. Записываются окончательные выражения для iL (t), uC (t)
9. Рассчитывается ток iR (t) = i 5(t) в цепи, не содержащей реактивных элементов.
Этот расчет следует проводить на основании законов Кирхгофа для послекоммутационной схемы. При этом считаются уже известными iL (t) и uC (t). Из второго уравнения системы (1)
Графики рассчитанных iL (t), uC (t) и i 5(t) приведены на рис. 7, 8.
10. По результатам расчета построить графики iL (t), uC (t), iR (t)
Рекомендуется построение графиков провести, используя графический редактор пакета MathCAD. В этом случае следует приложить распечатку графиков к заданию.
|
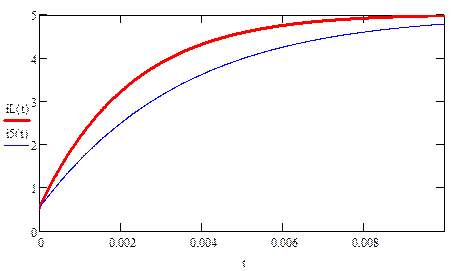
| рис. 7 |
|
| рис. 8 |
Операторный метод
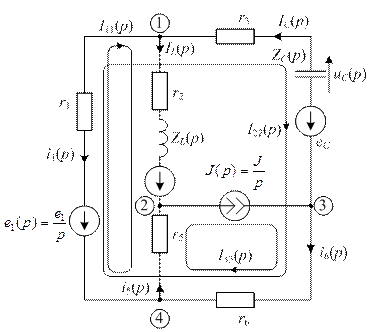
Расчет переходного процесса операторным методом следует начинать с составления операторной схемы после коммутации (рис. 9). При этом надо учесть, что в операторной схеме изображение по Лапласу постоянных источников имеет вид:
, 
Операторные сопротивления реактивных элементов в схеме:
, 
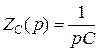
В операторной схеме появляются дополнительные источники ЭДС:
, 
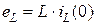Они включаются последовательно с операторными сопротивлениями ZL (p) и ZC (p). Направления стрелок этих источников: стрелка источника eL совпадает со стрелкой изображения тока в индуктивности IL (p), стрелка источника eC противоположна стрелке изображения тока в емкости IC (p).
Направление стрелок изображений токов в ветвях операторной схемы должны совпадать со стрелками токов-оригиналов, выбранных в послекоммутационной схеме при классическом методе расчета.
Числовые значения дополнительных источников eL и eC могут быть взяты из расчета классическим методом (iL (0), uC (0)).
;.
|
| рис. 9 |
Расчет операторной схемы можно провести, например, методом контурных токов I 11(p), I 22(p).
Так как в схеме есть источник тока, то следует ввести контурный ток
(6)
Операторный ток
Решение системы (6) дает выражение для операторного тока IL (p), представляемое как отношение двух полиномов с параметром p.
Можно получить это решение, используя процедуру символьного решения пакета MathCAD.
В этом случае рекомендуется в системе (6) подставить числовые значения параметров схемы.
(7)
Для символьного решения (7) в системе MathCAD необходимо воспользоваться решающим блоком
Given
система (7)
Find(I11,I22) → 
Знак равенства «=» в уравнениях (7) должен быть логическим. Стрелка «→» после набора оператора Find(I11,I22) выбирается из иконки «Панель символов»
MathCAD произведет решение и оно высветится на месте пунктира в фигурных скобках в виде матрицы-столбца. Верхняя строка этого столбца и есть операторное изображение для I 11(p) = IL (p).
Для определения оригинала iL (t) необходимо воспользоваться теоремой разложения.
Знаменатель изображения тока M (p) следует приравнять нулю и найти корни этого алгебраического уравнения. Затем следует продифференцировать знаменатель по аргументу p.
Тогда оригинал переходного тока
,
где p 1, p 2, p 3, … – корни знаменателя.
Для числовых данных задания вышеописанные операции дают следующие результаты.
:
Выражение в скобках совпадает с характеристическим уравнением при решении классическим методом, поэтому корни знаменателя,,.
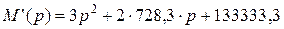
Если корни комплексно-сопряженные, то коэффициенты при экспонентах тоже будут комплексно-сопряженными, и тогда мнимые слагаемые в выражении для iL (t) уничтожаются.
По результатам численного расчета
;
Полученное выражение для iL (t) совпадает с расчетом классическим методом.
