2.3.1. Явный метод Рунге-Кутта 4-ого порядка.
Численные методы расчета переходных процессов предполагают представление системы дифференциальных уравнений Кирхгофа, записанных для схемы после коммутации в конечно-разностном виде. Представление временных производных в конечно-разностном виде в простейшем варианте соответствует так называемому методу ломаной Эйлера, но даже в этом случае возможны разные способы его реализации: явный и неявный метод Эйлера. При явном методе Эйлера приращение функции Δ y на интервале времени 
,
.
При этом значение 
в начале интервала 
, то есть в момент tk -1 считается известным. Например, для простейшего дифференциального уравнения
.
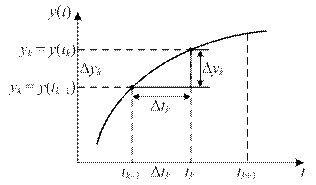
Такое представление соответствует так называемой правой производной (рис. 10).
|
| рис. 10 |
При явном методе Эйлера численное решение представленного дифференциального уравнения сводится к рекуррентной формуле
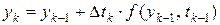
Такой способ решения приводит к накоплению ошибки округления и к концу переходного процесса может давать значительную погрешность.
При неявном методе Эйлера правая часть дифференциального уравнения определяется по заранее неизвестному значению искомой функции y (tk) в конце интервала времени Δ tk. В этом варианте используется так называемая левая производная при конечно-разностном ее представлении.
Неявный метод Эйлера обеспечивает меньшую погрешность округления, но более громоздок при численной реализации, так как требует предварительного определения неизвестной правой части уравнения.
Существуют улучшенные методы численного решения систем дифференциальных уравнений на основе явного метода Эйлера, обеспечивающие требуемую точность решения.
Наиболее распространенный из них является метод Рунге-Кутта. Современные программные системы имеют стандартные процедуры решения систем дифференциальных уравнений. В системе MathCAD процедура решения ДУ по методу Рунге-Кутта 4-ого порядка имеет вид:
S:=rkfixed(X,TO,Tmax,N,d),
где X – матрица-столбец неизвестных;
TO – начальное значение аргумента (начало переходного процесса, соответствующее моменту коммутации,);
Tmax – длительность переходного процесса;
N – число дискретных интервалов времени Δ t на отрезке Tmax;
d – матрица-столбец правой части решаемой системы дифференциальных уравнений, записанной в нормальной форме Коши.
Таким образом, для численного расчета переходного процесса в рассмотренной ранее схеме необходимо представить систему уравнений Кирхгофа (1) в нормальной форме.
Для этого необходимо свести систему (1) к двум уравнениям относительно тока iL (t) и напряжения uC (t) с учетом уравнений связи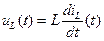 
, 
. Процедура сведения системы (1) к двум уравнениям, соответствует теоретическим положениям метода переменных состояния. Не вдаваясь в подробности этого метода проведем необходимые преобразования стандартными алгебраическими операциями.
Из первых трех уравнений системы (1) выразим i 1(t), i 5(t) и i 6(t)
.
После подстановки полученных выражений в (4) и (5) уравнения системы (1) получим:
После преобразований система дифференциальных уравнений в нормальной форме имеет вид:
или
, 
, 
, 
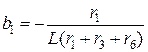Результаты расчета переходного процесса с помощью процедуры rkfixedприведены ниже.
В качестве начальных условий взяты значения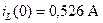 
и 
, рассчитанные ранее (п.2.1).
,,,, 
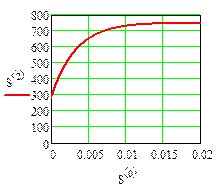
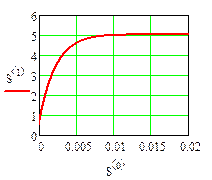
Графики iL (t) и uC (t) приведены на рис. 11
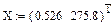
Напряжение на емкости  
Ток в индуктивности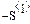  
 
|
| рис. 11 |
2.3.2. Метод дискретных резистивных схем.
Численный метод расчета переходного процесса в ЭЦ на основе неявного метода Эйлера сводится к расчету дискретной резистивной схемы. Такая схема получается для дискретного момента времени tk с учетом конечно-разностного представления производных в уравнениях Кирхгофа в послекоммутационном режиме.
Действительно, напряжение на индуктивности в момент времени tk
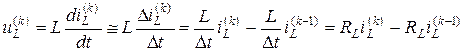
Полученное выражение соответствует замене в ЭЦ элемента индуктивности L источником напряжения 
и активным сопротивление RL (рис. 12)
|
| рис. 12 |
Дискретный резистивный элемент сопротивление и источник ЭДС 
заменяют в момент времени tk переходного процесса элемент индуктивность L.
Аналогичные выражения и схему замещения (рис. 13) можно получить для элемента емкость C.
|
| рис. 13 |
Дискретный резистивный элемент проводимость и источник тока 
заменяют в момент времени tk переходного процесса элемент емкость C.
В результате для дискретного момента времени tk будем иметь дискретную схему ЭЦ (рис. 14)
|
| рис. 14 |
Схема рис. 14 называется дискретной из-за наличия в ней дискретных источников 
и 
, значения которых изменяются на каждом последующем интервале времени Δ t переходного процесса.
Расчет переходных токов в этом случае сводится к решению системы линейных алгебраических уравнений Кирхгофа для дискретной схемы (рис. 14) на каждом интервале Δ t переходного процесса. Следовательно придется решать алгебраическую систему N раз, где N – количество дискретных интервалов времени Δ t, на которые разбит весь отрезок длительности процесса Tmax. При этом на первом интервале Δ t значения источников 
, 
определяются ННУ схемы. На каждом последующем интервале эти источники меняют свое значение, но матрица коэффициентов решаемой системы алгебраических уравнений не изменяется, меняется только матрица – столбец правой части системы.
Алгебраическая система уравнений Кирхгофа для дискретной схемы рис. 14 имеет вид:
1. 
2. 
3. 
4. 
5. 
6. 
В матричной форме система уравнений Кирхгофа примет вид
| i 1 | iL | iC | iGC | i 5 | i 6 |
,
В матричной форме
,
Решение матричного уравнения
Численная реализация описанного алгоритма приведена в системе MathCAD ниже
Начальные значения токов схемы рис. 14 взяты из расчета ЗНУ классическим методом. Значение начального тока iGc в дискретной схеме определяется по 1 закону Кирхгофа для узла †.
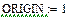
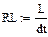
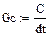
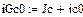
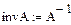
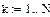
Результаты расчета аналитическими методами (классическим и операторным) и численными методами (Рунге-Кутта и дискретной схемы) абсолютно совпадают.
