Метричні та позиційні характеристики геометричних образів легко визначити при їх окремому положенні відносно площин проекцій. Оскільки на практиці геометричні образи найчастіше знаходяться в загальному положенні, треба їх привести з загального положення в окреме.
Метричні задач i зводяться до розв’язання чотирьох основних задач:
1) перетворення прямої загального положення в пряму рівня;
2) перетворення прямої загального положення в проекцiюючу;
З) перетворення площини загального положення в проекцiюючу;
4) перетворення площини загального положення в площину рівня.
 |
Метод заміни площин проекцій
На рис. 44 задано точку в системі площин проекцій П1 та П2. Проведемо вертикальну площину П4 яка перетнеться з площиною П1 по осі х14. Точку А спроекцiюємо на П4 прямою, перпендикулярною до П4 Таким чином, в системі взаємно перпендикулярних площин проекцій П1 i П4 матимемо дві проекції точки А — А1 та А4. Як видно з рисунка, при замiнi площини проекцій відстань вiд старої проекції А2 точки А до старої осi х12 дорівнює відстані від нової проекції А4 точки А до нової осі х14. На рис. 43, б цi ж дії повторені на комплексному рисунку. При розв’язаннi різних задач, переважно метричних, доводиться робити не одну, а дві, інколи навіть три заміни площин проекцій.
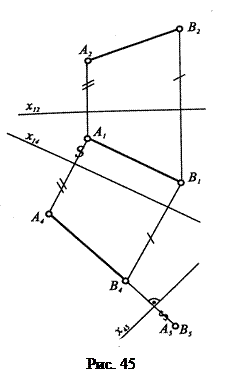
На рис. 45 однією заміною знайдена натуральна величина відрізка прямої АВ, для чого проведена проекціююча площина проекцій П4 паралельно горизонтальній проекції вiдрiзка, а щоб спроекцiюювати відрізок у точку, проведено площину П5 перпендикулярно до натурально величини i одержано проекцію вiдрiзка — А5В5.
Рис. 46 а ілюструє визначення відстані між двома мимобіжними прямими АВ та CD. з цією метою один з вiдрiзкiв CD двома замінами спроекцiюйовано в точку C5D5. Перпендикуляр, опущений з цієї точки на проекцію другої прямої — А5В5, i є шуканою відстанню.
Натуральна величина трикутного вiдсiку знайдена на рис. 46 б. Спочатку відсік поставлено у проекцiююче положення, для цього в ньому проведено горизонталь А i перпендикулярно до горизонтальної проекції горизонталі проведено площину П4, а потім паралельно лiнiйнiй проекції вiдсiку проведено площину П5. Натуральна вели8чина відсіку — трикутник А5 В5 С5.
Рис. 46 а ілюструє визначення відстані між двома мимобіжними прямими АВ та CD. з цією метою один з вiдрiзкiв CD двома замінами спроекцiюйовано в точку C5D5. Перпендикуляр, опущений з цієї точки на проекцію другої прямої — А5В5, i є шуканою відстанню.
Натуральна величина трикутного вiдсiку знайдена на рис. 46 б. Спочатку відсік поставлено у проекцiююче положення, для цього в ньому проведено горизонталь А i перпендикулярно до горизонтальної проекції горизонталі проведено площину П4, а потім паралельно лiнiйнiй проекцій вiдсiку проведено площину П5. Натуральна величина відсіку — трикутник А5 В5 С5.
 |
Метод плоско паралельне переміщення.
 |
Якщо в способі заміни площин проекцій геометричні образи вважаються зафіксованими в просторі, а до них певним чином проводяться нові площини проекцій, то в способі плоско паралельного переміщення все відбувається навпаки. Основні площини проекцій П1 та П2 вважаються зафіксованими в просторі, а геометричні образи обертаються певним чином, щоб перевести їх з загального положення в окреме. На рис. 47, а відрізок прямої загального положення АВ поворотом навколо вертикально осi i поставлений у положення, паралельне площині проекцій П2 при цьому він зобразиться в натуральну величину.
Але, як видно з рисунка, положення осі не має значення, досить роз ташувати, в даному випадку, горизонтальну проекцію вiдрiзка горизонтально, тобто паралельно П2, i на фронтальній проекції одержимо таку ж натуральну величину відрізка. На тому ж рисунку відрізок ще раз повернуто у вертикальне положення, при якому він на полі П1 спроекцiюється в точку =А1 =В1 Якщо перший поворот відрізка був здійснений навколо невиявленої горизонтально - проекцiюючої осі, то другий поворот — навколо невиявленої фронтально - проекцiюючої осі.
 |
У способі заміни площин проекцій наявність осей проекцій обов’язкова, тому що від них здійснюється відлік відстаней, а в способі плоско паралельного переміщення осі можна не фіксувати, бо вони не впливають на одержані результати.
 |
Натуральну величину трикутного відсіку АВС знайдено на рис.48. Для цього спочатку трикутник поставлено у проекцiююче положення, за допомогою проведено горизонталі DС трикутник повернуто навколо вертикальної невиявленої осі так, щоб горизонтальна проекція горизонталі розташувалася перпендикулярно до поля П2. При такому положенні горизонталь спроекцiюється в точку, а весь вiдсiк — в лiнiю –А2 –В2 –С2. Нарешті, лінійна проекція відсіку розташовується паралельно полю П1 при цьому відбувається обертання відсіку навколо фронтально проекцiюючої невиявленої осi. Трикутник =А1 =В1 =С1 є його натуральною величиною.
На рис. 49 способом плоско паралельного переміщення знайдено натуральну величину двогранного кута мiж двома трикутними відсіками зі спільним ребром АВ. Першим поворотом навколо вертикально не виявлено осi двогранний кут розташовано так, щоб його ребро АВ було паралельним полю П2 i зобразилося на ньому в натуральну величину. Другим поворотом навколо невиявленої фронтально проекцiюючої осі кут розташовується таким чином, щоб його ребро було вертикальним i спроекцiюювалося на П1 точку, а гранi двогранного кута — в лінію. Двогранний кут спроекцiюється при цьому в натуральну величину.
Питання для самоперевірки:
1. У чому полягає суть центрального проектування?
2. У чому полягає суть паралельного проектування?
3. Як називають і як позначають три основні площини проекцій?
4. Що таке комплексне креслення точки і як його отримують?
5. Сформулюйте основні положення проектування точки.
6. Як побудувати ортогональні проекції прямої лінії?
7. Яку пряму називають прямою загального положення?
8. Як на комплексному рисунку розташовуються її проекції?
9. Які прямі називають прямими окремого положення?
10. Як їх зображують на площинах проекцій?
11. Які випадки можливі відносного положення точки і прямої у просторі?
12. Як розташовуються проекції точки, що належіть прямій?
13. Які ви знаєте способи завдання площини на комплексному кресленні?
14. Які площини називають площинами рівня?
15. Які площини називають проектуючими площинами?
16. Які умови належності точки, прямої до площини?
17. На якій прямій лежатимуть конкуруючі точки двох профільних прямих?
18. Скільки параметрів визначають перетин прямої загального положення з проекціюювальною площиною?
19. Чому задача на перетин прямої з площиною вважається першою основною позиційною задачею?
20. Чи можна звести другу основну позиційну задачу до першої?
21. Як мають бути розміщені дві мимо6iжнi прямі загального положення, щоб відстань між ними зображувалась на одній з площин проекцій?
22. Чи може непрямий кут перетину двох прямих спроекцiююватися на одній із площин проекцій прямим кутом?
23. Скільки площин можна провести через довільну точку простору, перпендикулярних до даної прямої?
24. Скільки площин можна провести через довільну точку простору, перпендикулярних до даної площини?
25. Скільки потрібно параметрів, щоб побудувати перпендикуляр до площини загального положення з будь-якої точки?
26. Скільки параметрів визначають двогранний кут, перпендикулярний до однієї з площин проекцій
