Завдання 1 - Студент повинен заповнити аркуш написами згідно взірця. Він видається викладачем у термін проведення практичних занять,
Всі написи на кресленнях слід виконувати креслярським шрифтом відповідно ГОСТ2.304-81. У даному державному стандарті наведені основні відомості що до конструкції літер і цифр, установлено їх висоту, ширину, товщину, відстань між літерами та інші елементи, які дають змогу чітко, охайно і досить красиво виконувати написи.
Стандарт визначає такі розміри висот шрифту: h=40; 28; 20; 14; 10; 7; 5; 3,5; 2,5; 1,8, де h – висота великих літер та цифр у міліметрах, а висота малих літер відповідає наступному розміру шрифту. Наприклад, якщо шрифт №10 – означає, що висота великих літер та цифр дорівнює 10мм, а малих літер – 7мм
Рис. 6 - Взірець титульного аркушу.
. Стандарт визначає товщину лінії шрифту (позначимо - d) типом шрифту:
Тип А – без нахилу літер – d=1/14h;
Тип А – з нахилом літер під кутом 75° до горизонту – d=1/14h;
Тип Б – без нахилу літер – d=1/10h;
Тип Б – з нахилом літер під кутом 75° до горизонту – d=1/10h.
Таблиця 1. – Ширина літер
| Елемент шрифту | Ширина кожного елементу |
| Великі літери, крім букв А, Ж, Г, Е, З, С, М, Ц, Х, Д, Ф, Ш, Щ, Ю | 6/10h(де h – це висота шрифту) |
| Великі літери Г, Е, З, С | 5/10h |
| Великі букви А, М, Д, Х, Ц, Ю | 7/10h |
| Великі букви Ж, Ф, Ш | 8/10h |
| Велика літера Щ | 9/10h |
| Велика та мала літера І, і | 1/10h |
| Малі літери з, с | 4/10h |
| Малі літери, крім букв ж, м, т, ф, ш, щ, ю | 5/10h |
| Малі літери м, ю | 6/10h |
| Малі літери ж, т, ф, щ, ш | 7/10h |
При виконанні навчальних креслень рекомендовано використовувати шрифт типу Б з нахилом під кутом 75°, де висота великих літер h=10d, а висота малих літер 7/10h. Висота допоміжної сітки – 17/10h, відстань між літерами – 2/10h, відстань між словами – 6/10h, напис і співвідношення розмірів елементів літер та цифр наведені у таблиці 1. До іспиту треба зібрати три індивідуальні графічні роботи и виконати титульний лист.
АРКУШ № 1
Теоретична частина:
Нарисна геометрія вивчає способи побудови на площині зображень предметів, що мають три виміри. Для побудови зображень предметів на площині користуються методом проектування. Слово «проекція» - латинське, від дієслова projecere, що в перекладі означає "кинути наперед". Отже, проекція – це зображення предмета, "відкинуте" на площину за допомогою променів. Спроектувати предмет – це означає відобразити його на площині.
Проекції поділяються на центральні і паралельні. Ідея центрального проектування наведена на рис. 7 а.
 |
Рис. 7
Точка S, з якої виходять проекціюючі промені, називається – центром проекції. Площина П1, на яку проектується предмет, називається площиною проекцій. Площина П1 і точка S з проектуючими променям становлять апарат центральної проекції. Проектований трикутник ABC називається оригіналом або натурою. Щоб спроектувати трикутник, треба з центра проекцій S через усі його вершини провести проекціюючі промені до перетину з площиною проекцій П1. Точки перетину з площиною П1 називаються центральними проекціями вершин А, В, С на площину П1, а трикутник А1В1С1 – центральною проекцією трикутника АВС.
У нарисній геометрії користуються методом паралельного проектування (рис. 7 б). Вибирають площину проекцій П1, точка S – центр проекцій – віддалена в нескінченність і тому проекціюючі промені паралельні між собою. Площин П1 і напрям s становлять апарат паралельної проекції. Щоб спроектувати трикутник АВС на площину П1, проводять через вершини А, В, С проекціюючі промені паралельно напряму проектування s. Трикутник А1 В1 С1, утворений внаслідок перетину променів АА1, ВВ1, СС1 з площиною П1, є паралельною проекцією трикутника АВС.
Паралельні проекції поділяють на прямокутні і косокутні. Якщо промені перпендикулярні до площини проекцій (рис. 6 в), то такі проекції називають прямокутними або ортогональними. Якщо ж кут нахилу променів не дорівнює 900, то такі паралельні проекції називаються косокутними.
При виконанні креслень треба користуватися прямокутними проекціями на три площини проекцій.
Основні позначення та символи, які використовуються при виконанні контрольної роботи розділу «Нарисна геометрія»:
А, В, С, D..., 1, 2, 3,… - точки;
a, b, c, d - лінії прямі та криві,
в т. ч. h – горизонталь, f – фронталь, p – профільна пряма;
α,β,γ - площини; Φ,Σ,Λ, Ω - поверхні; α,β,γ - кути.
П – площина проекцій в загальному випадку;
П1 – горизонтальна площина проекцій;
П2 – фронтальна площина проекцій;
П3 – профільна площина проекцій;
П¢. – аксонометрична площина проекцій;
П4, П5, … - додаткові площини проекцій;
x, y, z, s - осі проекцій, вони супроводжуються індексами площин проекцій, які перетинаються по певній осі. Наприклад, x12, y13, z23.
Співвідношення між геометричними елементами, фігурами:
║ - паралельність (d ║l – лінії d та l взаємно паралельні);
≡ - збіг, тотожність (6 ≡ 5 – точки 6 та 5 збігаються);
¸ -мимобіжність (d ¸ l – лінії d та l мимобіжні);
- перпендикулярність (α 
β - площини α та β взаємно перпендикулярні);
- належність (F Φ - точка F належіть поверхні Φ);
∩ - перетин (S=h ∩ Q, точка S - результат перетину лінії h та площини Q).
Скористаємося трьома взаємно перпендикулярними площинами, що утворюють прямий тригранний кут (рис. 8 а). Тут П1 – горизонтальна, П2 – фронтальна і П3 – профільна площина проекцій; лінії Оx, Oy, Oz взаємного перетину площини проекцій – осі проекцій; точка О123 – початок осей проекцій.. Якщо з точки А проведемо проекціюючі промені АА1, АА2 і АА3, перпендикулярні до площин проекцій, до перетину з П1, П2, П3, отримаємо А1 – горизонтальну, А2 – фронтальну і А3 – профільну проекції точки А (рис. 8а).
Рис. 8.
Вважаючи тригранний кут розщепленим по осі Оy (рис. 8 б) і залишаючи нерухомою фронтальну площину проекцій П2, обертають горизонтальну площину П1 навколо осі Оx униз на 900, а профільну П3 – навколо осі Оz вправо на 900 до їх суміщення з фронтальною площиною проекцій. Таке утворення плоского креслення трьох площин проекцій разом з побудованими на них проекціями А1, А2, А3 точки А називають комплексним кресленням точки А. Пряма, що сполучає дві проекції точки на комплексному кресленні, називається лінією зв'язку. Тепер сформулюємо основні положення:
- Горизонтальна А1 і фронтальна А2 проекції точки розміщуються на одній вертикальній лінії зв'язку;
- Фронтальна А2 і профільна А3 проекції точки розміщуються на одній горизонтальній лінії зв'язку;
- Горизонтальна А1 і профільна А3 проекції точки розміщуються на лініях зв'язку, що перетинаються на бісектрисі кута y1O123y3. Ця бісектриса має назву постійної прямої креслення і позначається К123
Розглянемо на прикладі побудову проекцій точки за її координатами (рис. 9 а).
Усі величини розмірів наведені у міліметрах. Задано точку А (25, 15, 20), тобто x=25мм; y=15мм; z=20мм. Треба побудувати комплексне креслення точки А. На рис. 9 а показано, як це треба робити, а також побудовано комплексні креслення точок В (20, 0, 15) і С (15, 0, 0) на рис. 9 б.
 |
Рис. 9
Прямі в просторі діляться на прямі загального положення, прямі рівня і проекціюючі (перпендикулярні). Проекціюючими називають прямі, які перпендикулярні одній з площин проекцій, тобто паралельні двом іншим площинам (рис. 10). На одній з площин проекцій проекціююча пряма зображується у вигляді точки, а на двох інших – у вигляді відрізків, які займають горизонтальне або вертикальне положення, величина яких дорівнює натуральній величині відрізка прямої.
 |
Рис. 10 - Проекціюючі прямі:
 |
а)горизонтально - проекціююча; б)фронтально - проекціююча;
в)профільна – проекціююча.
Рис. 11 - Прямі рівня:
а)горизонтального; б)фронтального; в)профільного
Прямими рівня називають прямі, які паралельні одній з площин проекцій. На цю площину вони проектуються в натуральну величину, а на дві інші у вигляді горизонтальних або вертикальних відрізків менших розмірів (рис. 11).Пряма, яка паралельна горизонтальній площині проекцій П1, називається горизонтальною прямою або горизонталлю (рис. 11 а). Якщо пряма паралельна фронтальній площині проекцій П2, її називають фронтальною прямою або фронталлю (рис. 11 б). А якщо пряма паралельна профільній площині проекцій П3, її називають профільною прямою (рис. 11 в).
За рисунком прямої рівня можна визначити натуральну величину кутів нахилу прямої до площин проекцій:
j - кут нахилу прямої до горизонтальної площини проекцій;
y - кут нахилу прямої до фронтальної площини проекцій;
w - кут нахилу прямої до профільної площини проекцій.
Із розглянутого вище можна зробити висновок: якщо пряма займає положення, паралельне площині проекцій, то вона проектується на цю площину без викривлення, тобто проекція відрізка дорівнює самому відрізку прямої.
 |
Прямою загального положення називають пряму, яка похило розташована до всіх площин проекцій. Кожна її проекція менша самої прямої (рис. 12). Пряма загального положення похило розташована до усіх площин проекцій. Кожна її проекція менша самої прямої, викривлені і кути нахилу прямої до площин проекцій.
 |
Натуральна величина (Н.В.) відрізка прямої загального положення визначається гіпотенузою прямокутного трикутника, побудованого на одній з його проекцій як на катеті. Другий катет трикутника дорівнює різниці відстаней кінців відрізка від тієї самої площини проекцій, на якій взяли перший катет (рис. 13).
Кут між Н.В. відрізка прямої і її проекцією дорівнює куту нахилу прямої до відповідної площини проекцій. На рис. 13 показано визначення натуральної величини відрізка прямої загального положення і кута її нахилу до горизонтальної площини проекцій. Якщо необхідно визначити y - кут нахилу прямої до фронтальної площини проекції, то прямокутний трикутник треба побудувати на фронтальній проекції прямої. Величина другого катета дорівнює DУ=УA–УB. Для визначення кута w побудову прямокутного трикутника необхідно виконувати на профільній проекції, величина другого катета дорівнює: DХ=ХА-ХВ.
У просторі точка і пряма відносно друг друга може займати такі положення: точка належить прямій; точка не належить прямій. Якщо точка належить прямій, то її проекції належать однойменним проекціям прямої і знаходяться на одній лінії зв’язку (рис. 14). Точка D не належить прямій АВ, тому що її фронтальна проекція не належить фронтальній проекції цієї прямої. В даному випадку точка D знаходиться над прямою АВ.
Площину можна зобразити проекціями геометричних елементів, а саме:
· трьох точок, що не знаходяться на одній прямій (рис. 15,а);
· прямої і точки, яка не лежить на цій прямій (рис. 15,б);
· двох прямих, що перетинаються (рис. 15,в);
· двох паралельних прямих (рис. 15,г);
·
 |
відсік плоскої фігури, наприклад, трикутник (рис. 15,д).
За розташуванням у просторі розрізняються площини окремого і загального положення. В свою чергу площини окремого положення поділяються на площини рівня і проекціюючі.
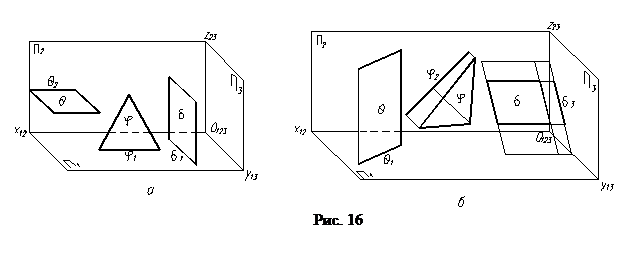
Площиною рівня (рис. 16, а) називається площина, яка паралельна одній з площин проекцій. Проекціюючою називається площина, яка перпендикулярна одній з площин проекцій (рис. 16, б). Загального положення називається площина, яка знаходиться під кутом до площин проекцій (П1, П2 П3).
 |
Пряма лежить у площині, якщо вона проходить через дві точки, що належать цій площині (рис. 17). Точка лежить у площині загального положення, якщо вона належить прямій, яка лежить у цій площині (див. точку К на рис. 17).
