Характерным примером явления самоиндукции служат так назы-ваемые токи замыкания и размыкания в электрических цепях постоян-ного тока. При включении (выключении) источника энергии возраста-ние силы тока при замыкании электрической цепи и убывание силы тока при ее размыкании происходит не мгновенно, а постепенно.
Представим себе, что мы замыкаем контур, в результате чего в нем возникает электрический ток. При этом магнитное поле тока возрастает, а следовательно, возрастает и поток магнитной индукции через пло-щадь, ограниченную контуром. Согласно правилу Ленца, возникающий индукционный ток будет создавать поток индукции, компенсирующий увеличение первоначального магнитного потока. Следовательно, инду-цируется ток, создающий магнитное поле, направленное противополож-но магнитному полю первоначального тока. Отсюда заключаем, что ин-дукционный ток направлен противоположно замыкаемому току. Этот индуцируемый ток обратного направления называется током замыка-ния. Ток замыкания уменьшает ток,идущий в контуре.Наличие токазамыкания приводит к тому, что нарастание тока в цепи при его вклю-чении происходит медленнее, чем при отсутствии тока.
Аналогичное явление мы наблюдаем при размыкании цепи. Если в контуре сила тока падает, то при этом уменьшается поток магнитной индукции через площадь, ограниченную контуром. В контуре инду-цируется ток, создающий по правилу Ленца поток индукции, увели-
| I 0− I |
чивающий уменьшающийся поток, т. е. индуцируется ток в том же направлении, в котором шел основной ток. Этот индуцируемый ток называется током размыкания. Ток размыкания направлен в ту же сторону, что и основной ток.
L

R
2
К
1 
 ε
ε
Рис. 3.5.1
Ток замыкания и размыкания можно наблюдать с помощью схемы, представленной на рис. 3.5.1, содержащей индуктивность L, не зависящую от силы тока I, сопротивление R и источник электро-энергии с э. д. с. ε.
Определим характер изменения силы тока при замыкании элек-трической цепи. Переведем переключатель К в положение 1. В этом случае в цепи будет действовать ЭДС ε источника и ЭДС самоин-
| дукции ε c = − L di. Тогда, благодаря явлению самоиндукции, полная | |||||||
| dt | IR =ε+εc=ε − L di | ||||||
| э. д. с. в контуре будет равна | , откуда сила тока в | ||||||
| контуре окажется равной: | dt | ||||||
| ε − L di | |||||||
| I = | dt | . | (3.5.1) | ||||
| ε | R | ||||||
| Замечая, что величина | = I 0 | – установившееся в цепи значение | |||||
| R | |||||||
силы тока, который протекал бы по контуру при отсутствии самоин-дукции, перепишем выражение (3.5.1) в виде:
| I 0− I = | L | dI . | (3.5.2) | |
| R dt |
Так как значение I 0 постоянно, то dI можно заменить на – d (I 0 – I), то-
гда d ( I 0 − I ) = − RL dt. Интегрируя обе части этого выражения, получим:


| ln(I 0 | − I) = − | R | t +ln C. | (3.5.3) | |
| L |
Произвольную постоянную ln С определим из условия, что I = 0 при t = 0, откуда ln C = ln I 0 и выражение (3.5.3) принимает вид:
| ln | I | − I | = − | R | t | ⇒ I 0− I = I 0 e | − | R | t | , | ||||||||||
| L | ||||||||||||||||||||
| I 0 | L | |||||||||||||||||||
| или окончательно получим: | ||||||||||||||||||||
| I = I 0(1− e | − | R | t | ) = | ε | (1 − e | − R t | ). | ||||||||||||
| L | L | |||||||||||||||||||
| R | ||||||||||||||||||||
(3.5.4)
(3.5.5)
Это выражение показывает, что при включении э. д. с. ток в цепи не сразу достигает значения I 0, но достигает его постепенно и теммедленнее, чем больше коэффициент самоиндукции контура L и чем меньше сопротивление контура R. Графически зависимость силы тока от времени при включении изображена на рис. 3.5.2, кривая 1. Теоре-тически ток должен достигнуть своего конечного значения I 0 лишь через бесконечно большой промежуток времени. Практически для обычных значений коэффициента самоиндукции L, ток достигает сво-его предельного значения весьма быстро.
I
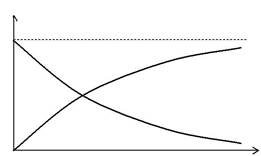
I 0
| 1 | ||||||
| 2 | ||||||
| t | ||||||
| Рис. 3.5.2 | ||||||
| Величина | L | = τ, имеющая размерность времени, называется по- | ||||
| R | ||||||
стоянной цепи.
Теперь рассмотрим случай размыкания цепи. Для этого переклю-чатель К (рис. 3.5.1) переведем из положения 1 в положение 2.
Чтобы выяснить характер тока размыкания, предположим, что в некотором контуре первоначально существовала э. д. с., которая под-держивала в нем силу тока I 0. Затем в момент времени, для которого мы примем t = 0, эта э. д. с. выключается, но контур остается замкну-
тым, причем полное сопротивление его равно R. Тогда в контуре ток прекратится не сразу, но будет продолжать идти еще некоторое время
за счет э. д. с. самоиндукции ε c = − L dI dt.
Сила тока самоиндукции определится законом Ома: I c = ε R c = − RL dI dt.

Это равенство можно переписать в виде: dII = − RL dt, что пред-


ставляет собой дифференциальное уравнение, определяющее зависи-мость силы тока самоиндукции от времени.
Интегрируя правую и левую части уравнения, получим:
| ln I = − R t + ln C, | (3.5.6) | |
| L |

где С − произвольная постоянная. Значение этой произвольной посто-янной получим из условия, что I = I 0 при t = 0, откуда: ln I 0 = ln C. Та-ким образом, получим:
| ln | I | = − | R | t,или I = I 0 e | − | R | t | . | (3.5.7) | |
| L | ||||||||||
| I 0 | L | |||||||||
Это соотношение показывает, что с ила тока при выключении э. д. с.
спадает по экспоненциальному закону,при этом спадает тем медлен-
нее, чем больше коэффициент самоиндукции L и чем меньше сопро-тивление R. Зависимость силы тока размыкания от времени графиче-ски представлена на рис. 3.5.2, кривая 2.
Время t 0, в течение которого сила тока размыкания спадает до поло-вины своей первоначальной величины, определится из соотношения
| R | I | 1 | L | ||||||
| I = I 0 e − | L | t, если в нем положить | = | , откуда t 0 | = ln 2 | . Скорость убы- | |||
| I 0 | R | ||||||||
вания определяется постоянной времени цепи: τ= RL. Величина τ есть

время, в течение которого сила тока уменьшается в e раз (е = 2,72 – осно-вание натурального логарифма).
| − R t | ε | − | R | t | ε | − | t | ||||||||
| I = I 0 e | L | = | e | L | = | e | τ . | (3.5.8) | |||||||
| R | R | ||||||||||||||
Существование токов размыкания позволило обнаружить явле-ние сверхпроводимости. При сверхпроводимости R → 0 и ток по-сле выключения э. д. с. будет продолжаться в контуре сколь угодно долго, не ослабевая. Опыты Каммерлинг − Оннеса, приведшие к от-
крытию сверхпроводимости, производились следующим образом: соленоид, концы которого были соединены друг с другом, поме-щался между полюсами электромагнита, после чего охлаждался жидким гелием до температуры, при которой материал его провода становился сверхпроводящим. Затем магнитное поле электромагни-та выключалось. При этом в соленоиде возникал индукционный ток. При обычных условиях этот ток прекратился бы через весьма малый промежуток времени. При наличии же сверхпроводимости он про-должал идти по соленоиду в течение многих часов, не обнаруживая заметного ослабления.






