Теорема Бетти (о взаимности работ). Рассмотрим два состояния упругой системы (рис. 3.6). Соответствующие им силы назовем силами первой и второй группы. Представим два варианта загружения балки.
Вначале статически приложим силы первой группы, затем их зафиксируем и добавим – также статически – силы второй группы. Очевидно, что процедура, показанная на рис. 3.5, является частным случаем рассматриваемой, поэтому по аналогии с формулами (3.6) и (3.7) суммарную работу нагрузки можно представить в следующем виде:
A I = A 11 + A 12 + A 22,
где A 11 – работа первой группы сил на вызванных ими перемещениях;
A 12 – работа первой группы сил на перемещениях, вызванных силами второй группы;
A 22 – работа второй группы сил на вызванных ими перемещениях.

Рис. 3.6
Во втором варианте загружения вначале статически приложим силы второй группы, затем их зафиксируем и добавим силы первой группы. В этом случае суммарная работа сил будет равна:
A II = A 22 + A21 + A 11.
Работа сил, приложенных к идеально упругому телу, не зависит от истории загружения и определяется только начальным и конечным состоянием системы, поэтому, приравнивая A I и A II, получим:
A 12 = A 21 . (3.8)
Итак, теорема Бетти утверждает, что работа первой группы сил на перемещениях, вызванных силами второй группы, равна работе второй группы сил на перемещениях, вызванных силами первой группы.
Поскольку работа внешних сил равна и противоположна по знаку работе внутренних сил: A = - W, теорема Бетти справедлива и для них:
W 12 = W 21 .
Отметим, что эта теорема является основной среди общих теорем строительной механики – две другие можно рассматривать как следствия теоремы Бетти.
Теорема Максвелла (о взаимности удельных перемещений). Рассмотрим два состояния упругой системы. Пусть первое из них представлено силой Pi = 1, приложенной в точке i, а второе – силой Pj = 1, приложенной в точке j (рис. 3.7).
| Pj =1 |
| Pi =1 |
| δ ji |
| δ jj |
| δ ij |
| δ ii |
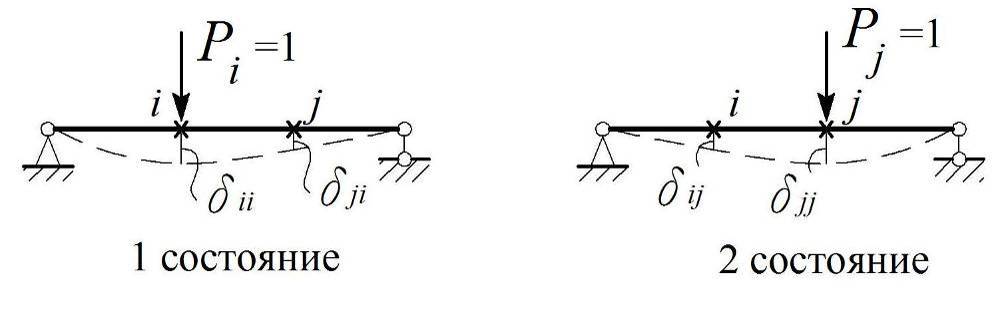
Рис. 3.7
Здесь и в дальнейшем удельные перемещения мы будем обозначать не заглавными буквами D i, а строчными – d i.
Поскольку перемещение всякой точки упругой системы пропорционально приложенной силе, между D ji на рис. 3.5, а и d ji на рис. 3.7 существует зависимость: D ji = Pi d ji или, сменив последовательность индексов на более привычную:
D ij = Pj d ij. (3.9)
Воспользуемся теоремой Бетти, записав формулу (3.8) в виде:
Pi d ij = Pj d ji .
Учитывая, что в последнем выражении Pi = Pj = 1, получим:
d ji = d ij. (3.10)
Итак, теорема Максвелла утверждает, что перемещение точки i от единичной силы, приложенной в точке j, равно перемещению точки j от единичной силы, приложенной в точке i.
Теорема Релея (о взаимности удельных реакций). Для СНС в качестве внешних сил, фигурирующих в теореме Бетти, могут выступать реакции, вызванные кинематическими воздействиями.
Рассмотрим два состояния упругой системы, где первое соответствует единичному смещению i -й моментной связи на левом конце балки, а второе – единичному смещению j -й линейной связи на ее правом конце. Обозначим через δ ij и q ij линейное перемещение и угол поворота i -й связи от единичного смещения j -й связи (рис. 3.8).
| 1 состояние |
| 2 состояние |
| rii |
| rji |
| rij |
| rjj |
| а) |
| б) |
| δ jj =1 |
| θ ii =1 |
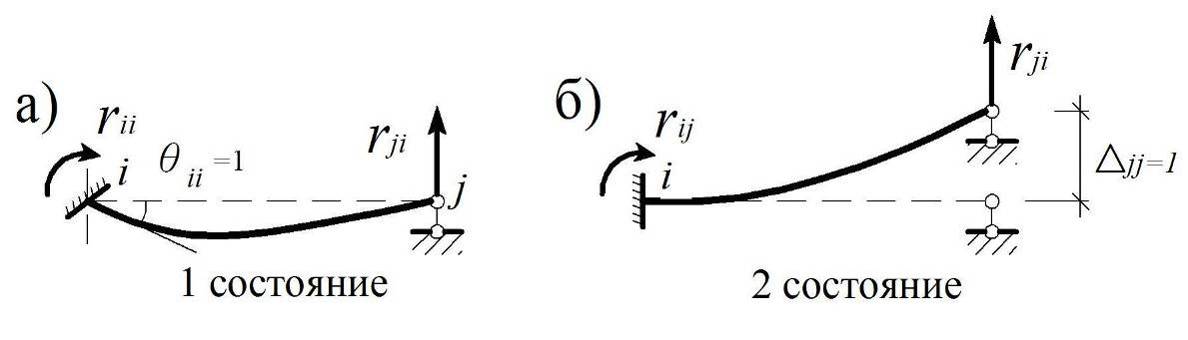
Рис. 3.8
Работа первой группы сил на перемещениях второго состояния системы будет равна:
A 12= rii × q ij + rji × δ jj = rii × 0 + rji × 1 = rji.
Аналогично находим работу второй группы сил на перемещениях первого состояния:
A 21= rij × q ii + rjj × δ ji = rij × 1 + rjj × 0 = rij.
Подставляя полученные выражения в (3.8), получим:
rij = rji . (3.11)
Таким образом, теорема Релея утверждает, что реакция i-й связи от единичного смещения j-й связи равна реакции j-й связи от единичного смещения i-й связи.
Примечания
1. Если вместо единичной силы в точке i приложить единичный момент, зависимость (3.10) примет вид:
d ij = q ij.
Как видим, удельные перемещения d ij могут иметь различную размерность. Проще всего ее найти из (3.9), принимая в этом выражении D ij за обобщенное перемещение, а Pj - за обобщенную силу. Тогда [d ij ] = [ D ij ] / [ Pj ] и мы получим:
а) для силы, приложенной в точке j:
– [d ij ] = м/Н, если D ij - линейное перемещение;
– [d ij ] = 1/Н, если D ij - угловое перемещение.
б) для момента, приложенного в точке j:
– [d ij ] = м/(Нм) = 1/Н, если D ij - линейное перемещение;
– [d ij ] = 1/(Нм), если D ij - угловое перемещение.
2. Приведенное доказательство теоремы Релея может показаться неубедительным. В самом деле, мы ссылаемся в нем на теорему Бетти, в которой рассматриваются два состояния одной и той же системы, загруженной различной нагрузкой. Можно ли это утверждать в отношении двух балок, изображенных на рис. 3.8, а и 3.8, б? Ответ на этот вопрос будет положительным, если учесть следующее:
а) принцип освобождаемости от связей справедлив в отношении как СОС, так и СНС;
б) если реакции связей СОС вторичны, то есть появляются только в ответ на действие активных сил и образуют с ними уравновешенную систему, то реакции связей СНС, вызванные кинематическими воздействиями, образуют самоуравновешенную систему сил;
в) напряженно-деформированное состояние заданной СНС, вызванное смещением i -й связи, тождественно НДС в эквивалентной упругой системе, полученной из заданной путем устранения этой i -й связи и загруженной активной силой, равной ее реакции.
Поскольку в нашем примере на рис. 3.8 речь идет о двух связях, для получения одной и той же системы нужно удалить обе. Если при этом число лишних связей заданной СНС будет меньше или равно двум, полученная система будет, очевидно, статически определимой или даже подвижной.
| rji |
| θ =1 |
| rii |
| δ =1 |
| rij |
| rjj |
| б) |
| а) |
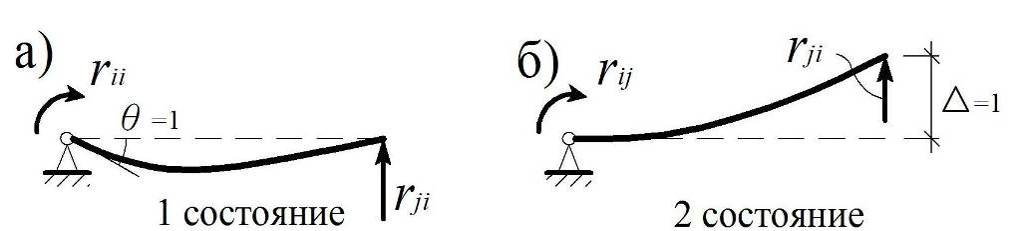
Рис. 3.9
Итак, действительно две балки на рис. 3.8, а и 3.8, б можно рассматривать как два состояния одной и той же системы (рис. 3.9, а, б).






