 |
На расстоянии R (рис. 2.1) на тело массой m действует сила
При перемещении этого тела на расстояние d R затрачивается работа
(2.1)
Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению (рис.2.1).
Если тело перемещать с расстояния R 1 до R 2, то затрачивается работа
(2.2)
Из формулы (2.2) вытекает, что затраченная работа в поле тяготения не зависит от траектории перемещения, а определяется лишь начальным и конечным положениями тела, т.е. силы тяготения действительно консервативны, а поле тяготения является потенциальным.
Работа совершаемая консервативными силами равна изменению потенциальной энергии системы, взятому со знаком минус, т.е.
(2.3)
Из формулы (2.2) получаем
При 
(
). Тогда (2.3) запишется в виде
Так как первая точка была выбрана произвольно, то
Величину
,
являющуюся энергетической характеристикой поля тяготения, называют потенциалом.
Потенциал поля тяготения j— скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность.
Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен
(2.4)
где R — расстояние от этого тела до рассматриваемой точки.
Рассмотрим взаимосвязь между потенциалом поля тяготения (j) и его напряженностью (g).Из выражений (2.1) и (2.4) следует, что элементарная работа dА, совершаемая силами поля при малом перемещении тела массой т, равна
С другой стороны,
где d l – элементарное перемещение.
Учитывая 
, получим, что
т.е.
или
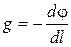
Величина 
характеризует изменение потенциала на единицу длины в направлении перемещений в поле тяготения.
Можно показать, что
(2.5)
где 
‑ градиент скаляра j.
Знак минус в формуле (2.5) указывает, что вектор напряженности g направлен а сторону убывания потенциала.
Рассмотрим потенциальную энергию тела, находящегося на высоте h относительно Земли:
где Rо - радиус Земли.
Так как
и 
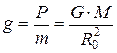(2.6)
то, учитывая условие h << R, получим
Таким образом, мы вывели формулу потенциальной энергии тела находящегося на высоте h над Землёй.
Космические скорости
Для запуска ракет в космическое пространство надо в зависимости от поставленных целей сообщать им определённые начальные скорости, называемые космические.
Первой космической (или круговой) скоростью u 1 называют такую скорость, которую надо сообщить телу, чтобы оно могло двигаться по круговой орбите, т.е. превратиться в искусственный спутник Земли.
На спутник, движущийся по круговой орбите радиуса r, действует сила тяготения Земли, сообщающая ему нормальное ускорение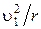 
. По второму закону Ньютона:
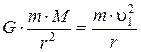
Если спутник движется недалеко от поверхности Земли, тогда 
(радиус Земли) и 
. Поэтому у поверхности Земли:
.
Второй космической (или параболической) скоростью u 2 называют ту наименьшую скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спутник Солнца, т.е. чтобы его орбита в поле тяготения Земли стала параболической.
Для того чтобы тело могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы его кинетическая энергия была равна работе, совершаемой против сил тяготения:
откуда 
.
Третьей космической скоростью u 3 называют такую скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы преодолев притяжение Солнца. Третья космическая скорость 
.
ОСНОВЫ ТЕРМОДИНАМИКИ
Законы идеального газа
В молекулярно-кинетической теории понятие идеального газа это:
§ собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда;
§ между молекулами газа отсутствуют силы взаимодействия;
§ столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Закон Бойля – Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объём есть величина постоянная:
при 
и 
Кривая, изображающая зависимость между величинами p и V при постоянной температуре называется изотермой (рис. 1.1).
Закон Гей – Люссака:
1. объём данной массы газа при постоянном давлении изменяется линейно с температурой:
при 
и (1.1)
2. давление данной массы газа при постоянном объёме изменяется линейно с температурой:
при 
и (1.2)
где t – температура по шкале Цельсия; V o и p o – объём и давление при 0оС;
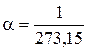К-1 – переводной коэффициент.
Процесс, протекающий при постоянном давлении, называется изобарным, а кривая изобарой (рис. 1.2).
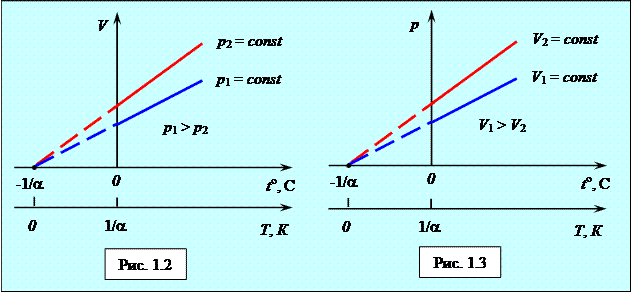Процесс, протекающий при постоянном объёме, называется изохорным, а кривая изохорой (рис. 1.3).
Изобары и изохоры пересекают ось температур в точке 
, оС, определяется из условия 
. Если перенести начало отсчёта в эту точку, то переходит переход к шкале Кельвина, откуда:
Используя уравнения (1.1) и (1.2), получим:
.
при и (1.4)
при и (1.5)
Закон Авогадро: моли любых газов при одинаковой температуре и давлении занимают одинаковые объёмы.
При нормальных условиях этот объём равен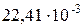 
м3/моль.
В одном моле различных веществ содержится одно и тоже число молекул, называемое постоянной Авогадро:
моль-1.
Закон Дальтона: давление смеси идеального газа равно сумме парциальных давлений p 1, p 2, …, p n входящих в неё газов:
Парциальное давление – давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объём, равный объёму смеси при той же температуре.
