Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества.
(Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза – вода; газообразная фаза – смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трехфазной, в которой лёд является твердой фазой. Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лёд, например, встречается в пяти различных модификациях – фазах).)
Переход вещества из одной фазы в другую – фазовый переход – всегда связан с качественными изменениями свойств вещества.
Различают фазовые переходы двух родов. Фазовый перед I рода (например, плавление, кристаллизация и т. д.) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода.
Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объёма, называются фазовыми переходами II рода. Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоёмкости. Согласно трактовки ученого Л.Д. Ландау фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода. Примерами фазовых переходов II рода являются: переход ферромагнитных веществ (железа, никеля) при определённых давлении и температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия (гелий I) при Т = 2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести.
ОПИСАНИЕ СВОЙСТВ ВЕКТОРНЫХ ПОЛЕЙ
Градиент.
Это понятие используется для описания скалярных полей. Если каждой точке P с координатами x, y, z значение скалярной величины j принимает различные значения 
, то говорят, что задано скалярное поле функции j.
Градиентом скалярной величины j называется вектор с компонентами:
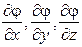
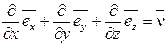
где 
– оператор набла (оператор Гамильтона)
Поток вектора.
Выберем поверхность S и разобьем на элементарные участки dS.
- поток вектора 
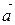через поверхность dS.
где 
‑ произвольное векторное поле;
dS – элементарная площадка;
– направление нормали к поверхности;
– псевдовектор.
где Ð a – угол между 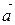и 
(т.е. )
Ф – поток вектора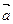 
через поверхность S.
(Направление выбирается произвольно. Линии поля это условный образ. Их густота, характеризует значение модуля данной физической величины).
Дивергенция.
Частное от деления потока Ф u на величину объема, из которого он вытекает, т.е. 
даёт удельную мощность источников, заключённых в объёме V. При стягивании объёма в точку P т.е.:
даёт истинную удельную мощность источников в точке P называемой дивергенцией (или расхождением) вектора .
 |
Аналогично определяется дивергенция любого вектора :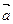
.
