Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты,— невозможен.
(Для иллюстрации этого положения рассмотрим работу теплового двигателя (исторически второе начало термодинамики и возникло из анализа работы тепловых двигателей)).
Принцип действия теплового двигателя приведен на рис. 6. От термостата с более высокой температурой Т1, называемого нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, называемому холодильником, за цикл передается количество теплоты Q2, при этом совершается работа A = Q1 - Q2.
 |
Чтобы термический коэффициент полезного действия теплового двигателя был h = l, должно быть выполнено условие Q 2 = 0, т. е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Так, французский физик и инженер Н. Л. С. Карно (1796—1832 гг) показал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами, иначе это противоречило бы второму началу термодинамики.
Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип действия которой представлен на рис. 7. Системой за цикл от термостата с более низкой температурой T2 отнимается количество теплоты Q2 и отдается термостату с более высокой температурой T1 количество теплоты Q1.
Для кругового процесса, согласно, Q = A, но, по условию, Q = Q2 - Q 1 < 0, поэтому А <0 и Q 2 ‑ Q 1 = - А, или Q 1 = Q 2 + А, т. е. количество теплоты Q 1, отданное системой источнику теплоты при более высокой температуре Т 1, больше количества теплоты Q2, полученного от источника теплоты при более низкой температуре T2, на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать её более нагретому телу. Это утверждение есть не что иное, как второе начало термодинамики в формулировке Клаузиуса.
Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T1) и холодильников (T2), наибольшим к.п.д. обладают обратимые машины; при этом к.п.д. обратимых машин, работающих при одинаковых температурах нагревателей (T1) и холодильников (T2), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами).
Карно теоретически проанализировал обратимый наиболее, экономичный цикл, состоящий из двух изотерм и двух адиабат, и называемый циклом Карно. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.
Цикл Карно изображен на рис. 8, где изотермические расширение и сжатие заданы соответственно кривыми 1 – 2и 3 – 4,аадиабатические расширение и сжатие – кривыми 2 – 3и 4 – 1. При изотермическом процессе U =const, поэтому, количество теплоты Q1, полученное газом от нагревателя, равно работе расширения A12, совершаемой газом при переходе из состояния 1 в состояние 2:
(2.27)
 |
При адиабатическом расширении 2 – 3теплообмен с окружающей средой отсутствует и работа расширения A23 совершается за счет изменения внутренней энергии:
(2.28)
Количество теплоты Q2, отданное газом холодильнику при изотермическом сжатии, равно работе сжатия A34:
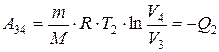(2.29)
Работа адиабатического сжатия:
(2.30)
Работа, совершаемая в результате кругового процесса,
А = A12 +A23 +A34 +A41 = Q1 + A23 ‑ Q2 ‑ A23 = Q1 ‑ Q2
и, как можно показать, определяется площадью на рис. 8.
Термический к.п.д. цикла Карно
(2.31)
Применив уравнение (
) для адиабат 2 ‑ 3 и 4 ‑ 1, получим
, 
откуда
(2.32)
Подставляя (2.27) и (2.29) в формулу (2.31) и учитывая (2.32), получим:
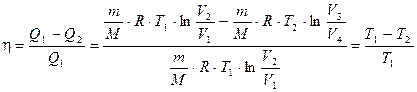
т. е. для цикла Карно к.п.д. действительно определяется только температурами нагревателя и холодильника. Для его повышения необходимо увеличивать разность температур нагревателя и холодильника. Например, при T 1 =400 K и Т 2 = 300 К h = 0,25. Если же температуру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то h = 0,5. (К.п.д. всякого реального теплового двигателя из-за трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.)
(Обратный цикл Карно лежит в основе действия тепловых насосов. В отличие от холодильных машин тепловые насосы должны как можно больше тепловой энергии отдавать горячему телу, например системе отопления. Часть этой энергии отбирается от окружающей среды с более низкой температурой, а часть — получается за счет механической работы, производимой, например, компрессором.)
Теорема Карно послужила основанием для установления термодинамической шкалы температур. Сравнив левую и правую части формулы (59.4), получим
т. е. для сравнения температур Т 1 и Т 2 двух тел необходимо осуществить обратимый цикл Карно, в котором одно тело используется в качестве нагревателя, другое — холодильника.
Из равенства видно, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному. Согласно теореме Карно, химический состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шкала не связана со свойствами какого-то определенного термометрического тела. Отметим, что практически таким образом сравнивать температуры трудно, так как реальные термодинамические процессы являются необратимыми.
§ 8. Уравнение Ван-дер-Ваальса
Учитывая собственный объем молекул и сил межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальса вывел уравнения состояния реального газа, введя две поправки:
1. Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический - свободный объем, в котором могут двигаться молекулы реального газа, будет не Vт, а Vт ‑ b, где b – объем, занимаемый самими молекулами.
2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е.
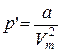(8.1)
где а – постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vт – молярный объем.
Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):
(8.2)
Для произвольного количества вещества n газа (n = т/М)с учетом того, что V = n×Vm, уравнение Ван-дер-Ваальса примет вид
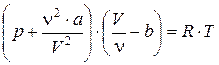
или
.
где поправки а и b – постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).
Изотермы Ван-дер-Ваальса
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса — кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса (8.2) для моля газа (рис. 9.1).
При высоких температурах (Т>ТК) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением её формы, оставаясь монотонно спадающей кривой. При некоторой температуре Тк на изотерме имеется лишь одна точка перегиба K. Эта изотерма называется критической, соответствующая ей температура Тк – критической температурой. Критическая изотерма имеет одну точку перегиба K, называемую критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V к и давление P к называются также критическими. Состояние с критическими параметрами (Р к, V к, Тк ) называется критическим состоянием. При низких температурах (Т<.ТК) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно опускаясь.
 |
Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса (8.2) к виду
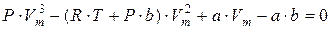(9.1)
Уравнение (9.1) при заданных P и T является уравнением третьей степени относительно V m, следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причём физический смысл имеют лишь вещественные положительные корни.
Поэтому первому случаю соответствуют изотермы при низких температурах три значения объема газа V 1, V 2и V 3 отвечают одному значению давления P 1, второму случаю — изотермы при высоких температурах.
 |
Таким образом, истинная изотерма будет иметь вид ломаной линии 7 - 6 - 2 - 1. Часть 7 - 6 отвечает газообразному состоянию, а часть 2 - 1 - жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6 - 2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
