Модели в механике. Системы отсчёта.
Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.
Механика, для описания движения использует разные физические модели. Простейшей моделью является материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь.
Под воздействием тел друг на друга тела могут деформироваться, т.е. изменять свою форму и размеры. Поэтому в механике вводится ещё одна модель – абсолютно твёрдое тело. Абсолютно твёрдое тело – тело, которое не подвержено деформации.
Любое движение твёрдого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом отсчета.
В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами х, y и z или радиусом-вектором r, проведенным из начала системы координат в данную точку (рис. 1).
 |
При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями:
; 
; 
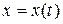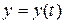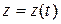; (1.1.)
эквивалентными векторному уравнению:
. (1.2.)
Уравнения (1.1) и соответственно (1.2) называются кинематическими уравнениями движения материальной точки.
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то, как уже было сказано, она обладает тремя поступательными степенями свободы (координаты х, y и z); если она движется по некоторой поверхности, то двумя степенями свободы, если вдоль некоторой линии, то одной степенью свободы.
Исключая t в уравнениях (1.1.) и (1.2.), получим уравнение траектории движения материальной точки. Траектории движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 1.2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути DS и является скалярной функцией времени: 
. Вектор 
, проведенный из начального положения движущейся точки в положение её в данный момент времени, называется перемещением.
 |
Скорость
Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.
Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор 
(рис. 2.1). В течение малого промежутка времени Dt точка пройдёт путь DS и получит элементарное перемещение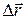 
.
 |
Вектором средней скорости 
называется отношение приращения 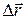радиуса-вектора точки к промежутку времени Dt.
(2.1)
Направление вектора средней скорости совпадает с направлением 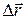. При неограниченном уменьшении Dt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью 
:
или 
.
Таким образом, модуль мгновенной скорости равен первой производной пут по времени:
(2.2.)
Мгновенная скорость 
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 2.2.
 |
Если выражение ds=u×dt (см. формулу (2.2)) проинтегрировать по времени в пределах от t до t + D t, то найдем длину пути, пройденного точкой за время D t:
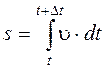(2.3)
В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид
Длина пути, пройденного точкой за промежуток времени от t1 до t2, дается интегралом
.
