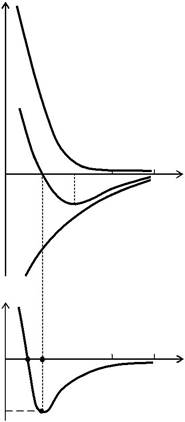
Экспериментальные и теоретиче-ские исследования показывают, что между атомами и молекулами вещества на малых расстояниях действуют силы отталкива-ния F o, а на больших − силы притяжения F п(рис. 13.1.1, а).Эти силы являются ре-зультатом квантовомеханического взаи-модействия элементарных частиц (элек-тронов, протонов), из которых состоят эти атомы или молекулы. В случае простых неполярных веществ притяжение в основ-ном обусловлено взаимодействием наве-денных дипольных моментов молекул. Эти сравнительно слабые ван-дер-ваальсовы силы зависят от расстояния r между молекулами по степенному закону
Изотермы газа Ван-дер-
F о, F п, F
F о a
F
r 0 rm
r
F п
б
| (F ≈ r−n) и, следовательно, носят коротко- | r 0 | C r | ||
| действующий характер. Область их дейст- | A D | |||
| вия порядка 10−9 м, т. е. на расстояниях, | W min | |||
| больших нм, эти силы практически равны | B | |||
| нулю. Переход от отталкивания на малых | ||||
| Рис. 13.1.1 |
расстояниях к притяжению на больших расстояниях способствует появлению минимума на кривой зависимо-
сти потенциальной энергии W взаимодействия двух частиц от расстоя-ния r между ними (рис. 13.1.1, б). На расстоянии r 0, которое соответст-вует минимуму потенциальной энергии, сила взаимодействия F обра-щается в нуль. Положение минимума определяет равновесное расстоя-ние для системы из двух частиц. Для двух молекул простых веществ
явный вид потенциальной энергии Ф(r) взаимодействия, которое опи-сывается потенциалом Леннарда − Джонса, имеет вид
| σ 12 | σ 6 | (13.11) | ||||
| Ф (r)=4ε | − | . | ||||
| r | r | |||||
Значения величин ε и σ, которые являются параметрами этого потенциала, можно определить в результате обработки эксперимен-тальных данных о термодинамических свойствах каждого отдельного вещества. Они содержатся в различных справочниках.
Наличие сил притяжения и отталкивания приводит к тому, что при больших давлениях (когда расстояние между молекулами умень-шается) поведение реального газа будет отличаться от модели идеаль-ного газа. Одно из наиболее известных приближенных уравнений описывающих состояние реального газа было предложено голланд-ским физиком Ван-дер-Ваальсом. Это уравнение базируется на законе Менделеева − Клапейрона и содержит два параметра (а и b), с помо-щью которых учитывается вклад сил притяжения на больших рас-стояниях и сил отталкивания на малых расстояниях между молекула-ми реального газа.
Силы отталкивания противодействуют проникновению данной частицы в ту область объема сосуда, которая занята другими молеку-лами. Собственный объем V 0, занятый частицей, представляется как объем шара с некоторым эффективным диаметром d. Поэтому «сво-бодный объем» V *,в котором могут свободно(как в идеальном газе)двигаться молекулы реального газа, будет на некоторую величину меньше, чем объем V, занимаемый газом. «Свободный объем» будет равен
| V *= V −ν b, | (13.1.2) |
где b − поправочный коэффициент для одного моля газа. Приближенные расчеты показывают, что объем, занятый моле-
кулой, равен учетверенному собственному объему этой молекулы V 0. Тогда поправка b равна
| b = 4 Na V 0. | (13.1.3) |
Наличие сил притяжения между молекулами приводит к допол-нительному «внутреннему» давлению рi, которое оказывается обратно пропорциональным квадрату V
| p |
| связаны уравнением Кла- |
| (13.1.6) |
| получаем |
| (13.1.7) |
| p =ν2 | a | , | (13.1.4) | |||
| i | V 2 | |||||
где a − второй поправочный коэффициент.
В результате внешнее давление р, которое необходимо прило-жить к реальному газу для удержания его в заданном объеме V, уменьшается по сравнению с давлением р * в случае идеального газа. Это значит, что
| p = p *− p = p *− ν2 | a | . | (13.1.5) | |||
| i | V 2 | |||||
Свободный объем V * и давление р * пейрона − Менделеева
р * V *=ν RT.
Подставляя в (13.1.6) выражения (13.1.2) и (13.1.5),
приближенное уравнение состояния для реального газа
p +ν2 Va 2(V − ν b)=ν RT.

Следует отметить, что уравнение Ван-дер-Ваальса лучше согласуется с опытными данными, чем уравнение Клапейрона −Менделеева, особенно при
 больших давлениях. больших давлениях.
| К | |||
| Проведем анализ уравнения Ван- | ||||
| p 4 | ||||
| дер-Ваальса. С этой целью построим зави- | ||||
| симости давления от объема газа при по- | p 1 | T 4 | ||
| стоянной температуре для нескольких зна- | T 3 | |||
| чений температуры (Т 1 < Т 2 < Т к < Т 3 < Т 4). | T К T 2 | T 1 | ||
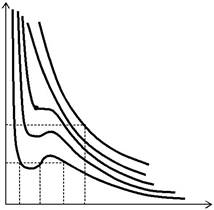
| Результаты представлены на рис. 13.1.2. | V 1′ V 1′′ V 1′′′ V * | |||
| V | ||||
| Полученные кривые − изотермы Ван- | ||||
| Рис. 13.1.2 | ||||
| дер-Ваальса,оказываются довольно |
своеобразными: при низких температурах они имеют волнообразные участки (максимумы и минимумы), при некоторой температуре Т к на изотерме имеется только точка перегиба К, при высоких температу-рах изотермы Ван-дер-Ваальса похожи на изотермы идеального газа.
С математической точки зрения такой характер изотерм объясня-ется очень просто. Если привести уравнение Ван-дер-Ваальса к нор-
мальному виду, то оно окажется кубическим уравнением относительно объема V. Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный корень и два мнимых. Очевидно, что первому случаю соответствуют изотермы при низких температурах (три значения объема газа V 1′, V 1′′, V 1′′′ отвечают одному значению давления
p 1),а второму случаю−изотермы при высоких температурах(одно зна-чение объема V 4 отвечает одному значению давления р 4) (рис. 13.1.2).






