Изучали диаметр цветка у микровишни в зависимости от 4 факторов: 1) принадлежность к виду (микровишня араксинская и микровишня седая), ареал распространения (Армения, Туркмения, Азербайджан, Грузия), популяция (всего 9 популяций) т генотип сеянца (32 сеянца):
| Вид (А) | Ареал (В) | Популяция (С) | Сеянец (D) | Диаметр цветка, мм | ||||
| M.araxina | Армения | P1 | ||||||
| P2 | ||||||||
| Туркмения | P3 | |||||||
| P4 | ||||||||
| M.incana | Азербайджан | P5 | ||||||
| P6 | ||||||||
| Грузия | P7 | |||||||
| P8 | ||||||||
| P9 | ||||||||
Определите доли влияния вида, ареала, популяции и генотипа сеянца на диаметр цветка у микровишни.
1. Копируем исходные данные в программу Excel.
2. Строим дисперсионный комплекс:
3. Вычислим основные параметры, суммы и компоненты формул:
Объем комплекса (N)=___________________
Число градаций по фактору А (а)=_________
Среднее число градаций по фактору В (b), приходящихся на одну градацию фактора А = 
Среднее число градаций по фактору С (с), приходящихся на одну градацию фактора В = 
Среднее число градаций по фактору D (d), приходящихся на одну градацию фактора C = 
Среднее число набл. на градацию факт. А 
Среднее число набл. на градацию факт. В 
Среднее число набл. на градацию факт. С 
Среднее число набл. на градацию факт. D 
| А | В | С | D | Диаметр цветка, мм | Σi….. | ni….. | xi….. | Σ.j…. | n.j.... | x.j.... | Σ..k.. | n..k.. | x..k.. | Σ…l. | n…l. | x…l. | Σ….. | n….. | x….. | ||||
| M.araxina | Армения | P1 | |||||||||||||||||||||
| P2 | |||||||||||||||||||||||
| Туркмения | P3 | ||||||||||||||||||||||
| P4 | |||||||||||||||||||||||
| M.incana | Азербайджан | P5 | |||||||||||||||||||||
| P6 | |||||||||||||||||||||||
| Грузия | P7 | ||||||||||||||||||||||
| P8 | |||||||||||||||||||||||
| P9 | |||||||||||||||||||||||
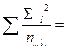
4. Суммы квадратов отклонений (SS):
Проверка корректности вычислений:
 |
5. Числа степеней свободы (df):
 | ||
 |
 |
 |
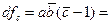
Проверка корректности вычислений:
6. Средние квадраты (ms):
7. Критерии Фишера (F):
8. Стандартные значения критерия Фишера:
для фактора А (dfa =____; dfb =____): F05 =______; F01 =______;
для фактора В (dfb =____; dfc =____): F05 =______; F01 =______;
для фактора C (dfc =____; dfd =____): F05 =______; F01 =______;
для фактора D (dfd =____; dfz =____): F05 =______; F01 =______.
9. Сравнение эмпирических значений критерия Фишера со стандартными:
FA =______ ___ F05 =______;
FB =______ ___ F05 =______9; FB =______ ____ F01 =_______;
FC =______ ___ F05 =______;
FD =______ ___ F01 =______.
10. Статистические выводы:
по фактору А:_________________________________________________________________;
по фактору В:_________________________________________________________________;
по фактору С:_________________________________________________________________;
по фактору D:_________________________________________________________________.
11. Дисперсии (σ2):
 | |||
 | |||
 |
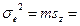
12. Доли влияния факторов:
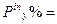
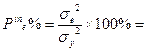
13. Ошибки групповых средних (mx), вычисляются только для тех средних, по которым доказано достоверное влияние фактора:
14. Критерий Тьюки (Q05):
групповые средние фактора В: Q05 (b=____; dfZ=____)=______
групповые средние фактора D: Q05 (b=____; dfZ=____)=______
15. Наименьшая существенная разность (НСР05):
для средних фактора В: НСР05= 
для средних фактора D: НСР05=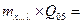 
16. Результативная таблица: ____________________________________________
__________________________
| Источник вариации | SS | df | ms | σ2 | F | F05 | F01 | Pin% | НСР05 |
| Общая | |||||||||
| Вид (А) | |||||||||
| Ареал (В) | |||||||||
| Популяция (С) | |||||||||
| Сеянец (D) | |||||||||
| Случайная |
17. Гистограммы групповых средних:
Рис. 4. Групповые средние по градациям фактора B
Рис. 5. Групповые средние по градациям фактора D
18. Круговая диаграмма долей влияния факторов
Ри.с 6. Доли влияния факторов
Матрица разностей между групповыми средними по фактору D
19. Сравнение групповых средних между собой:
