Целью является формирование:
1. Способности работать самостоятельно, забота о качестве, стремление к успеху (ОК-6)
2. Способности порождать новые идеи (ОК-5)
3. Умения ориентироваться в современных алгоритмах компьютерной математики, совершенствовать, углублять и развивать математическую теорию, лежащую в их основе (ПК-7)
4. Умения делать самостоятельный анализ физических аспектов в классических постановках математических задач (ПК-4)
5. Умения определять общие формы закономерностей, инструментальных средств для групп дисциплин (ПК-10)
Теоретические основы
Вывод уравнений
Уравнение Хопфа. Рассмотрим одномерную среду, состоящую из частиц, движущихся но инерции (т.е. без взаимодействия и в отсутствии внешних сил). Обозначим u (t, x) — скорость частицы, находящейся в момент времени t в точке х. Если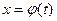 
— траектория движения некоторой фиксированной частицы, то ее скорость — 
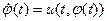, ускорение же 
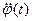равно нулю. Значит,
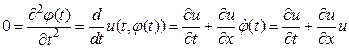
Полученное уравнение
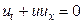(1)
описывающее эволюцию поля скоростей и невзаимодействующих частиц, и называется уравнением Хопфа.
Уравнение неразрывности. Это уравнение, которое выводится в курсе механики сплошной среды, описывает движение жидкости (или газа) в 
при отсутствии источников и стоков. Обозначим v (x, t) = 
— вектор скорости движения жидкости,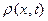 
— ее плотность. Зафиксируем произвольную область 
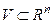. В момент времени t масса жидкости, содержащейся в этой области равна
,
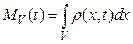скорость изменения этой массы есть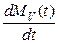 
. С другой стороны, при отсутствии источников и стоков внутри V, изменение массы 
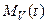происходит только от втекания и вытекания жидкости через границу 
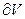рассматриваемой области, то есть скорость изменения массы 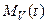равна потоку жидкости через :
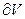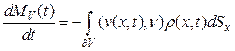
Здесь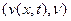 
— скалярное произведение вектора скорости v и вектора единичкой внешней нормали 
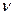к границе в точке 
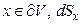— элемент площади на .
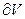Таким образом, имеем:
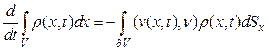
В предположении, что 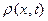и и достаточно гладки, преобразуем правую часть последнего равенства по формуле Гаусса-Остроградского (интеграл от дивергенции но некоторой области равен потоку через ее границу):
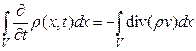(2)
где div — оператор дивергенции по пространственным переменным. Напомним, дивергенцией векторного поля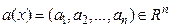 
называется скалярная величина
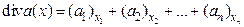
В силу произвольности области 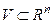, из равенства (2) приходим к хорошо известному в гидродинамике уравнению неразрывности:
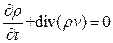. (3)
Уравнение просачивания воды через песок. Для упрощения введем несколько естественных ограничений. Предположим, что вода двигается под действием только силы тяжести, т.е. движение вертикальное и от горизонтальных координат зависимости нет. Источники и стоки отсутствуют, а скорость просачивания v есть функция плотности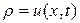 
, т.е. v = v (u).
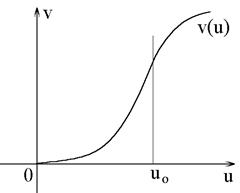рис.1
|
Экспериментально установлено, что зависимость v (u) выглядит так, как изображено на рис. 1. На отрезке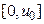 
с хорошей точностью можно считать, что эта зависимость почти параболическая, т.е. 
.
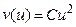В рассматриваемом одномерном случае уравнение (3) перепишется в виде
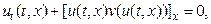(4)
или
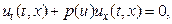
где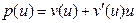 
. Вспоминая об экспериментально найденной зависимости скорости просачивания от плотности, считаем 
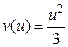, и окончательно имеем:
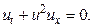
Уравнение дорожного движения. Это уравнение, как и уравнение фильтрации, получается из одномерного но х уравнения неразрывности (3). В задачах дорожного движения используют экспериментально найденную зависимость скорости движения автомобилей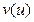 
от плотности 
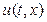машин на автостраде в данной точке. Типичная модель дорожного движения задается формулой
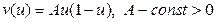
В этом случае уравнение (4) принимает вид
