Целью является формирование:
1. Способности работать самостоятельно, забота о качестве, стремление к успеху (ОК-6)
2. Способности порождать новые идеи (ОК-5)
3. Умения ориентироваться в современных алгоритмах компьютерной математики, совершенствовать, углублять и развивать математическую теорию, лежащую в их основе (ПК-7)
4. Умения делать самостоятельный анализ физических аспектов в классических постановках математических задач (ПК-4)
5. Умения определять общие формы закономерностей, инструментальных средств для групп дисциплин (ПК-10)
Решение типовых заданий
Пример 1. Популяция бактерий растет так, что скорость ее роста в момент t (время выражается в часах) равна размеру популяции, поделенному на 10. Описать этот процесс роста дифференциальным уравнением. Каков порядок этого уравнения?
Решение. Определим х (t) как размер популяции бактерий в момент времени t. Тогда по условию скорость роста 
в момент t равна 0,1 x (t),
т. е. = 0,1 x (t), Это дифференциальное уравнение первого порядка для х (t).
Ответ: 
Пример 2. Логистический рост. Скорость роста популяции в расчете на одну особь представляет собой разность между средней рождаемостью и средней смертностью. Будем считать, что средняя рождаемость выражается положительной постоянной b не зависящей от времени t и размера популяции х (t). Допустим также, что средняя смертность пропорциональна размеру популяции и потому равна х (t), где d — положительная постоянная. Это увеличение смертности с ростом популяции может происходить благодаря эффектам скученности или усиливающейся конкуренции за доступные пищевые ресурсы. В данной модели уравнение, которому подчиняется рост популяции, имеет вид
, или 
.
Разделяя переменные, получаем 
. Замечая, что
; и интегрируя, получим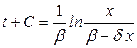 
Таким образом, если х (0) есть размер начальной популяции, то 
. Тогда для решения х (t)имеем соотношение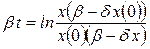 
. Переходя к экспонентам, получаем 
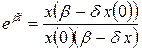. Наконец, выражая отсюда x (t),запишем решение в виде 
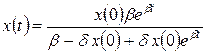. Процесс роста, описываемый такой функцией, называется логистическим ростом, а уравнение — логистическим.
Ответ: 
Пример 3. Найти кривые, у которых подкасательная равна сумме абсциссы и ординаты точки касания.
По условию отрезок проекции касательной АМ на ось ОХ есть подкасательная и равен АМ 1 (рис.). Тогда, если точка М имеет координаты 
, то выполняется равенство
, или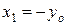 
.
|
Точка А (х 1, 0) удовлетворяет уравнению касательной к кривой 
, тогда 
. С учетом найденного соотношения 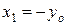получаем дифференциальное уравнение 
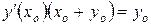. Так как рассуждения проводились относительно произвольной точки М, то индекс «0» можно опустить, имеем
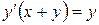или 
.
Полученное уравнение является однородным. Введя новую переменную z = 
, 
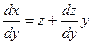получаем уравнение с разделяющимися переменными 
. Интегрируя обе части равенства, получим ln Су = z. Возвращаясь к прежней переменной, получим решение
.
Задания к вариантам для самостоятельных работ
1. Задача 1. Цилиндрический резервуар с диаметром 4 м имеет в длину 6 м. За сколько времени вода, наполняющая резервуар, вытечет через круглое отверстие в дне радиусом 1/12 м, если: а) ось цилиндра вертикальна; б) ось цилиндра горизонтальна? Скорость истечения воды из отверстия считать равной 
, где g - ускорение силы тяжести, h - высота уровня жидкости над отверстием.
Задача 2. Тело совершает 90 колебаний в минуту; амплитуда колебаний уменьшилась вдвое в течение 15 сек. Найти дифференциальное уравнение движения.
Задача 3. Рост, выживание и деление клеток определяются потоком питательных веществ через оболочку клетки. Это означает, что на ранних стадиях клеточного роста увеличение массы клетки пропорционально площади ее поверхности. Если во время роста форма и плотность клетки не изменяются, то масса клетки х (t)в момент t пропорциональна кубу радиуса, в то время как площадь поверхности пропорциональна квадрату радиуса клетки. Убедитесь в том, что на ранних стадиях роста х (t)удовлетворяет уравнению первого порядка.
2. Задача 1. За сколько времени заполнится резервуар (см. задачу 1 из первого варианта), поставленный вертикально, если наряду с истечением жидкости в него втекает вода со скоростью 10 м3 в 1 мин?
Задача 2. Найти закон прямолинейного движения, если известно, что работа действующей силы пропорциональна времени, протекшему с начала движения.
Задача 3. В некоторых химических реакциях отдельные продукты могут выступать катализатором своего собственного образования. х (t) — количество такого продукта в момент t, в данной модели реакция заканчивается, когда х = с,по-видимому, в результате исчерпания одного из компонентов реакции. Выразите общее решение через постоянные r — коэффициент пропорциональности, с - положительная постоянная и х (0).
3. Задача 1. В резервуаре находится 100 л рассола, содержащего 10 кг растворенной соли. Вода вливается в резервуар со скоростью 3 л в 1 мин. Смесь вытекает из него со скоростью 2 л в 1 мин. Концентрация раствора поддерживается равномерно посредством перемешивания. Сколько соли будет содержать резервуар по истечении часа?
Задача 2. Согласно наблюдениям, скорость роста популяции бактерий в момент t (время t выражается в часах) равна размеру популяции х (t), поделенному на 5. Опишите этот процесс роста дифференциальным уравнением для х (t).
Задача 3. В модели эпидемий один зараженный индивидуум вводится в сообщество, состоящее из п индивидуумов, восприимчивых к заболеванию. Определим х (t)как численность незараженных индивидуумов в популяции в момент t. Если предположить, что инфекция распространяется на всех восприимчивых к заболеванию, то х (t)будет убывать от начального значения х (0) = п до нуля r — положительная постоянная, характеризующая скорость заражения. Найдите решение этого уравнения, когда скорость распространения эпидемии максимальна.
4. Задача 1. После собрания воздух в зале вместимостью 10800 м3 содержит 0,12 % СО2. Сколько кубических метров воздуха, содержащего 0,04 %СО2, надо ежеминутно доставлять в зал, чтобы по истечении 10 мин содержание углекислоты в нем было 0,06%?
Задача 2. Дрожжи в растворе сахара растут таким образом, что их масса увеличивается со скоростью, равной половине массы в момент t (время выражается в часах).Опишите изменение массы дрожжей с помощью дифференциального уравнения. Каков порядок этого дифференциального уравнения?
Задача 3. Найти дифференциальное уравнение софокусных эллипсов с заданным фокусным расстоянием 2 с. Указание. Уравнение семейства 
, где a - произвольный параметр, дифференцируем по х, после сокращений имеем: 
. Исключив из этих двух уравнений а 2, получим искомое уравнение первого порядка.
5. Задача 1. Кирпичная стена имеет 30 см толщины. Найти, как зависит температура от расстояния точки до наружного края стены, если температура равна 20о на внутренней и 0о на внешней поверхности стены. Найти также количество тепла, которое стена (на 1 м2) отдает наружу в течение суток. Коэффициент теплопроводности k считать равным 0,0015.
Задача 2. В эксперименте с голоданием масса испытуемого за 30 дней уменьшилась со 140 до 110 фунтов. Ежедневные потери массы, согласно наблюдениям, были пропорциональны массе испытуемого. Какому дифференциальному уравнению удовлетворяет масса испытуемого как функция времени? Найдите массу испытуемого после 15 дней голодания.
Задача 3. Найти кривую, проходящую через точку (2,0) и такую, что отрезок касательной между точкой касания и осью ОУ имеет постоянную длину, равную 2.
6. Задача 1. Найти кривую, у которой площадь криволинейной трапеции с основанием [ а, х ] равна 
-й части пощади прямоугольника с тем же основанием и высотой, равной крайней ординате.
Задача 2. При выращивании в идеальных условиях популяции мух возрастали бы экспоненциально с постоянной а, равной 0,1, если время выражается в днях. Допустим, что начальная популяция состоит из 100 особей, и они выращиваются в идеальных условиях. Найдите размер популяции после; а) 10? б) 20; в) 50 дней роста.
Задача 3. Найти кривую, обладающую свойством: если через любую ее точку провести прямые, параллельные осям координат до встречи с этими осями, то площадь полученного прямоугольника делится кривой на две части, отношение площадей которых равно т/п.
7. Задача 1. Найти закон изменения силы тока в цепи с сопротивлением R и самоиндукцией L, если начальная сила тока равна I о, а электродвижущая сила меняется по закону 
.
Задача 2. Пусть Т (t) — разность в температуре объекта и окружающей его среды в момент времени t. Закон Ньютона утверждает, что при охлаждении скорость изменения этой разности температур пропорциональна самой разности. Это означает, что Т (t) удовлетворяет дифференциальному уравнению первого порядка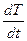 
= — kT,где k — положительная постоянная, характерная для данного объекта и окружающей его среды.
а) Выразите через k продолжительность времени, необходимого для того, чтобы первоначальная разность температур уменьшилась вдвое.
б) Вычислите время, через которое разность температур уменьшится до 1/4 своего начального значения.
Задача 3. Найти кривые, у которых длина подкасательной постоянна и равна а. Подкасательной называется отрезок проекции касательной на ось ОХ от точки касания с кривой до точки пересечения касательной с осью ОХ.
8. Задача 1. На тело действует сила, пропорциональная времени. Кроме того, среда сопротивляется движению тела с силой, пропорциональной скорости. Найти закон движения тела.
Задача 2. Рассмотрим ген с двумя аллелями А и а, которые в некоторой популяции в момент времени t представлены с частотами р (t) и q (t) = 1 — р (t). Предположим, что аллель А матирует в аллель а в единицу времени с вероятностью p. Это означает, что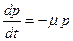 
. Постоянная 
называется частотой мутаций.
а) Выразите р (t) и q (t)через , если в начальный момент р (0) = q (0) = 0,5.
б) Выразите через время, необходимое для того, чтобы р (t) уменьшилось до 0,3.
Задача 3. Найти кривые, у которых длина поднормали постоянна и равна р. Поднормалью кривой называется отрезок проекции нормали на ось ОХ от точки кривой, к которой проведена нормаль до точки пересечения нормали с осью ОХ.
9. Задача 1. В резервуаре объемом 100 л находится рассол, содержащий 10 кг соли. Вода втекает в резервуар со скоростью 3 л в минуту, смесь с той же скоростью перекачивается во второй резервуар той же емкости, первоначально наполненный чистой водой. Избыток жидкости из него выливается. Каково максимальное количество соли во втором резервуаре и когда оно достигается?
Задача 2. Мутации между аллелями А и а могут происходить как в прямом, так и в обратном направлении с частотой прямых мутаций и частотой обратных мутаций v. Это означает, что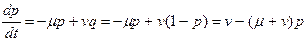 
а) Выразите р (t)и q (t)через р (0), q (0), и v.
б) Докажите, что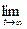 
р (t) = 
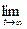, g (t) = 
(Равновесные частоты генов).
|
Задача 3. Найти кривые, у которых поднормаль равна сумме абсциссы и ординаты точки касания.
10. Задача 1. Ребенок, идущий по тротуару, везет по мостовой за собой тележку по траектории (см. рис.). Найти линию, по которой она движется (трактриса).
Задача 2. Выход вещества S в одной химической реакции составляет r молей в минуту. В то же время оно расходуется со скоростью с молей в минуту на каждый моль S. Определим S (t)как число молей вещества, имеющегося в момент времени t.
а) Составьте дифференциальное уравнение, которому удовлетворяет S(t).
б) Решив это дифференциальное уравнение, выразите S(t)через S(0).
в) Докажите, что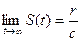 
. (Это равновесное количество вещества.)
Задача 3. Найти кривую, все касательные к которой проходят через начало координат.
11. Задача 1. Тело падает с высоты h под действием силы тяжести. Сопротивление воздуха пропорционально (коэффициент пропорциональности равен k) скорости падения. Найти закон движения тела.
Задача 2. В популяцию большого размера занесено инфекционное заболевание. Доля людей, перенесших заболевание, возрастает со временем. Пусть р (t)обозначает долю людей, переболевших этой болезнью за t лет после ее возникновения в популяции, и пусть р' (t) = [1 — р (t)] b. Найдите р (t)для всех моментов t > 0, если р (0) = 0. За сколько лет доля переболевших достигнет 90%?
Задача 3. Найти кривую, у которой поднормаль равна разности радиус-вектора и абсциссы точки касания.
12. Задача 1. Сила, натягивающая пружину, пропорциональна увеличению ее длины и равна 1 кг, когда длина увеличивается на 1 см. К пружине подвешен груз весом 2 кг. Найти период колебательного движения, которое получит груз, если его слегка оттянуть книзу и затем отпустить.
Задача 2. Потребление сигарет на душу населения в Соединенных Штатах возросло с 50 шт. в 1900 г. до 3900 шт. в 1960 г. (данные приблизительные). Считая, что рост потребления сигарет подчиняется логистическому[1] уравнению и что предельное потребление составляет 4000 шт., оцените уровень потребления в 1910, 1920, 1930, 1940 и 1950 гг.
Задача 3. Найти кривые, у которых нормаль совпадает с радиус-вектором точки касания.
13. Задача 1. Моторная лодка весом 300 кг движется прямолинейно с начальной скоростью 16 м/сек. Сопротивление воды пропорционально скорости движения и равно 10 кг при скорости 1 м/сек. Какое расстояние пройдет лодка, прежде чем ее скорость станет 8 м/сек, и в какое время пройдет оно это расстояние?
Задача 2. Популяция бактерий возрастает от начального размера в 100 ед. до предельного (равновесного) размера в 100 000 ед. Пусть в течение первого часа она увеличивается до 120 ед. Считая, что рост популяции подчиняется логистическому1 уравнению, найдите ее размер как функцию времени.
Задача 3. Определить кривые, у которых отрезок касательной от точки касания М до пересечения с осью ОХ равен отрезку оси ОХ, отсекаемому касательной от начала координат.
14. Задача 1. Корабль движется по прямой (которую можно принять за ось Ох) с постоянной скоростью v 1. Его преследует другой корабль с постоянной скоростью v 2, в начальный момент времени находящийся на расстоянии а от первого по перпендикуляру к его пути. Преследующий корабль постоянно держит курс на преследуемого. Найти уравнение линии движения преследующего корабля ("линия погони").
Задача 2. 30. Бактерии, служащие пищей для популяции простейших, поступают в экспериментальную среду с постоянной скоростью w. Установлено, что они потребляются со скоростью, пропорциональной квадрату их концентрации. Выразите концентрацию бактерий с (t).
Задача 3. Составить уравнение кривых, касательная к которым образует постоянный угол a с радиус-вектором из начала координат; проинтегрировать это уравнение, в интеграл ввести полярные координаты.
15. Задача 1. Снаряд вылетает из орудия со скоростью v о под углом 45о к горизонту. Масса снаряда равна т. Сопротивление воздуха пропорционально квадрату скорости полета (коэффициент пропорциональности равен k). На какую высоту поднимется и какое расстояние пролетит снаряд по горизонтали за время t?
Задача 2. Два вещества С1 и С2, участвуя в химической реакции в равных количествах, дают соединение С3. Пусть а и b обозначают начальные концентрации (в момент t = 0) веществ С1 и С2. Определим х (t)как концентрацию С3 в момент t. Найдите концентрацию С3 как функцию времени при t > 0, если х (0) = 0.
Задача 3. Найти линии, пересекающие кривые семейства под заданным углом:
а)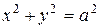 
под углом a. в) 
под углом 45о.
б) 
под углом 45о. г) 
под углом 45о.
Практическое занятие № 9
