Если результаты символьных вычислений включают в себя функции, не содержащиеся во входном языке системы, они помещаются в буфер обмена по запросу системы и могут быть вызваны оттуда командой Paste (Вставить) меню Edit (Правка). Вставленные из буфера результаты имеют статус текстовых комментариев, то есть проводить с ними дальнейшие действия в явном виде невозможно. Однако это вовсе не означает, что такие результаты бесполезны. Напротив, пользователь, владеющий приемами аналитических вычислений, может успешно привлекать такие результаты для решения серьезных математических задач. Здесь мы остановимся на задаче получения аналитического решения для линейных дифференциальных уравнений.
Способность Mathcad выполнять символьные (аналитические) преобразования открывает широчайшие возможности. Однако полагаться на эту способность «без оглядки» нельзя. В противном случае возможны грубые ошибки и горькие разочарования. Распознать ошибки могут только пользователи, хорошо владеющие хотя бы основами математики. Помните, что Mathcad помогает в решении ваших задач, а вовсе не решает их вместо вас.
Приведенные рассуждения поясняют технику применения системы Mathcad для решения ДУ различного вида и различными методами. Этот материал, однако, никоим образом не следует рассматривать как учебное описание математических методов решения ДУ. Предполагается, что эти методы знакомы студенту из курса математического анализа.
Теоретические вопросы, выносимые на обсуждение
1.Дать определение дифференциальных уравнений п -го порядка.
2.Дать определение системы п дифференциальных уравнений первого порядка.
3.Сформулируйте задачу Коши для системы п дифференциальных уравнений первого порядка.
4.Как задаются начальные условия для системы п дифференциальных уравнений первого порядка.
5.В какой форме должны быть записаны дифференциальные уравнения для его решения в среде Mathcad.
6.Как преобразовать дифференциальное уравнение n -го порядка в систему уравнений первого порядка.
7.Перечислите, какие вы знаете функции в Mathcad, позволяющие решать дифференциальные уравнения.
8.Опишите действие операции rkadapt (y, x l, x 2, acc, n, F, k, s) и каждого компонента, входящего в нее.
9.Опишите действие операции Rkadapt(y, x l, x 2, n, F) и каждого компонента, входящего в нее.
10. Опишите действие операции rkfixed(y, x l, x 2, n, F) и каждого компонента, входящего в нее.
11. Дайте определение фазового пространства.
12. В чем преимущества использования функции Rkadapt.
13. В каком случае используется функция Bulstoer (у, x l, х 2, n, F).
14. Какой численный метод реализует функция rkfixed.
15. Какой численный метод реализует функция Bulstoer.
16. Куда помещаются результаты символьных вычислений, включающие в себя функции, не содержащиеся во входном языке системы.
17. Как и с помощью каких команд можно вызвать результаты символьных вычислений, включающие в себя функции, не содержащиеся во входном языке системы.
18. Какой статус имеют вставленные из буфера результаты.
19. Можно ли проводить какие-либо вычислительные действия в явном виде с текстовыми комментариями.
Задания к вариантам для самостоятельных работ
I Исследовать на устойчивость нулевое решение, изобразить траектории движений, определяемые этой системой, указав на рисунке стрелками направление движения при возрастании времени. Определить тип особой точки
1. 
| 2. 
| 3. 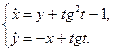
| 4. 
|
5. 
| 6. 
| 7. 
| 8. 
|
9. 
| 10. 
| 11. 
| 12. 
|
13. 
| 14. 
|
II Решить систему уравнений и показать интегральные кривые в декартовой системе координат
1. 
| 2. 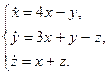
| 3. 
| 4. 
|
5. 
| 6. 
| 7. 
| 8. 
|
9. 
| 10. 
| 11. 
| 12. 
|
13. 
| 14. 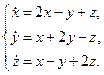
|
III Решить уравнение:
1. 
| 2. 
| 3. 
| 4. 
|
5. 
| 6. 
| 7. 
| 8. 
|
9. 
| 10. 
| 11. 
| 12. 
|
13. 
| 14. 
|
IV Найти общее решение линейного дифференциального уравнения
1. 
| 2. 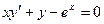
| 3. 
| 4. 
|
5. 
| 6. 
| 7. 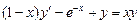
| 8. 
|
9. 
| 10. 
| 11. 
| 12. 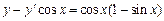
|
13. 
| 14. 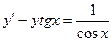
|
Практическое занятие № 6






