Производные высших порядков. Если функция 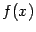дифференцируема при всех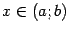, то мы можем рассмотреть функцию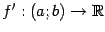, сопоставляющую каждой точке значение производной

Если функция дифференцируема при всех , то мы можем рассмотреть функцию , сопоставляющую каждой точке значение производной 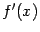. Эта функция называется производной функции 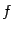, или первой производной от 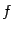. (Иногда саму исходную функцию 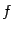называют нулевой производной и обозначают тогда 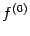.) Функция 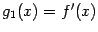, в свою очередь, может иметь производную во всех (или некоторых) точках интервала 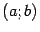, которую мы обозначим и назовём второй производной функции 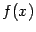. Если предположить, что вторая производная 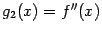существует во всех точках 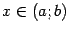, то она может также иметь производную , называемую третьей производной функции 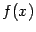, и т. д. Вообще, -й производной функции 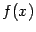называется производная от предыдущей, -й производной :

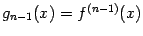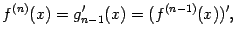
Теорема Ролля

Если вещественная функция непрерывна на отрезке [ a; b ] и дифференцируема на интервале (a; b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю

Теорема Лагранжа (обобщение теоремы Ролля)

y = f (x) – непрерывна при х Î [ a; b ] и

дифференцируема при х Î (a; b) Þ

$ c Î (a; b):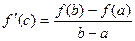

Теорема Коши

Пусть даны две функции и такие, что:

1. и определены и непрерывны на отрезке ;

2. производные 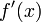и конечны на интервале ;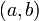

3. производные 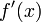и не обращаются в нуль одновременно на интервале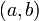

4. ;

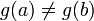тогда

, где

(Если убрать условие 4, то необходимо усилить условие 3: g'(x) не должна обращаться в ноль нигде в интервале (a, b).)

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f (a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а 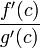равна как раз необходимому числу.

Лагра́нжа о среднем значении

утверждает, что если функция f непрерывна на отрезке [ a; b ] и дифференцируема в интервале (a; b), то найдётся такая точка 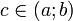, что

.

Геометрически это можно переформулировать так: на отрезке [ a; b ] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Исследование функции

Пусть дана функция 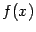. Для её исследования нужно:

1). Найти её область определения 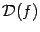. Если это не слишком сложно, то полезно найти также область значений 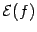. (Однако, во многих случаях, вопрос нахождения 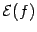откладывается до нахождения экстремумов функции.)

2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной (быть может, после сдвига влево или вправо по оси 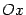), не является ли она периодической.

3). Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения 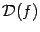, если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.