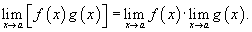если 
, то функция f называется бесконечно большой при x → x 0.
| |||
Ограниченная функция
Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x), 
лежит в полосе c ≤ y ≤ C.
loadGraphImg ("../../../../content/grapher/screensh/01030503.jpg", 350, 350, '', 'content/grapher/01030503.set', 'graph01030503', '', '', ''); 
Свойства бесконечно малых функций
| 1. | 
|
| 2. | 
|
| 3. | 
|
| 4. | 
|
Произведение
Произведение бесконечно малой функции 
при 
и функции 
, ограниченной в некоторой 
-окрестности точки a, есть функция бесконечно малая.
Доказательство. Функция является ограниченной в некоторой окрестности точки a и, следовательно, существует такое число B > 0, что
| (4) |
для всех x, удовлетворяющих условию
| (5) |
Поскольку функция является бесконечно малой при , то для любого произвольно малого числа ε > 0 существует такое число 
, что неравенство
| (6) |
выполняется для всех x, удовлетворяющих условию
| (7) |
Выберем из чисел и наименьшее и обозначим его символом δ. Тогда условие
| (8) |
является более сильным, чем условия (5) и (7) и поэтому влечет неравенства (4) и (6).
Таким образом, для любого произвольно малого числа ε > 0 выполняется неравенство
для всех x из δ-окрестности точки a.
Сумма
Сумма двух бесконечно малых функций есть функция бесконечно малая.
Доказательство. Пусть ε > 0 – произвольно малое число; и 
– бесконечно малые функции при 
. Тогда существуют такие положительные числа и , что условия
| (9) |
и
|
| (10) |
влекут за собой соответствующие неравенства
и
Если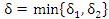 
, то условие перекрывает оба условия (9) и (10) и, следовательно,
Следствие. Сумма любого конечного числа бесконечно малых функций есть функция бесконечно малая.
Теорема о двух милиционерах
Если функция y = f (x) такая, что 
для всех x в некоторой окрестности точки a, причем функции φ(x) и ψ(x) имеют одинаковый предел при 
, то существует предел функции y = f (x) при , равный этому же значению, то есть
32. Вторая теорема Вейерштрасса
Непрерывная на отрезке [ a, b ] функция ограничена и достигает на этом отрезке своей верхней и своей нижней грани
Доказательство. Пусть f (x)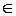 
C[ a, b ] (функция принадлежит классу непрерывных функций на отрезке [ a, b ]) и пусть 
.
Согласно определению верхней грани функции, для каждого n существует такая точка хn 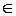[ а, b ], что
,
Из последовательности xn 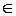[ а, b ] можно выделить сходящуюся к некоторому значению х 0 подпоследовательность:
.
В силу непрерывности функции имеем далее
.
В то же время
.
И в пределе f (x 0) 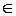M. Но f (x 0) не может быть больше верхней границы М и, следовательно, f (x 0) = М. Что и требовалось доказать
Свойства пределов функции
1) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы:
Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:
