Пусть
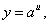
где a – положительное число, u – дифференцируемая функция x. Найдём производную y по x. Прологарифмируем обе части равенства по основанию e: ln y = u ln a. Дифференцируя это равенство по x и учитывая, что ln y – сложная функция, а ln a – постоянный множитель, получим
или
Подставив в последнее равенство
окончательно находим
Производная логарифмической функции
Производная функции y = ln x существует и выражается формулой
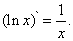(15)
В случае сложной логарифмической функции y = ln u, где u – дифференцируемая функция аргумента x, формула (15) примет вид
(16)
Пользуясь формулой (16), найдём производную логарифмической функции с произвольным положительным основанием a. Пусть
На основании свойств логарифмов имеем
Так как
- постоянный множитель, то
или
38.
Производные элементарных функций:
| Функция | Производная |
| f(x) = C, C ∈ R | 0 (да-да, ноль!) |
| f(x) = xn | n · xn − 1 |
| f(x) = sin x | cos x |
| f(x) = cos x | − sin x |
| f(x) = tg x | 1/cos2 x |
| f(x) = ctg x | − 1/sin2 x |
| f(x) = ln x | 1/x |
| f(x) = loga x | 1/(x · ln a) |
| f(x) = ex | ex |
Производная сложной функции
Пусть функция f: [ a, b ] → [ c, d ], а функция g:[ a 1, b 1] → [ c 1, d 1], причём [ a 1, b 1] 
[ c, d ]. Если функция f дифференцируема в точке х 0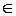 
[ a, b ], а функция g дифференцируема в точке y 0 = f (x 0) 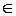[ a 1, b 1], то сложная функция F (x) = g (f (x)) имеет в точке х 0 производную, равную
g ' (f (x 0))· f ' (x 0).
Показательно-степенная функция
Показательно-степенной функцией называется функция вида y = uv, где u=u(x), v=v(x).
Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции.
Производная обратной функции
Теорема. Пусть функция х = f (y) монотонна и дифференцируема в некотором интервале (a, b) и имеет в точке у этого интервала производную f' (y), не равную нулю. Тогда в соответствующей точке х обратная функция у = f--1 (x) имеет производную [ f--1 (x)] ', причем
или 
Производные обратных тригонометрических функций
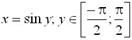
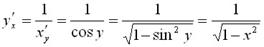
Производная функций заданных неявно
Если функция y=y(x) задана неявно уравнением F(x,y)=0, F(x,y) — дифференцируемая функция и F ' y(x, y) не равен 0, то производная y'(x) вычисляется по формуле y'(t) = - F'x(x, y) / F'y(x, y).
Производная функций заданных параметрически
формула производной параметрически заданной функции 
Дифференциал функции
Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f’(x)dx.
Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)’dx = u’dx ± v’dx = du ± dv
2) d(uv) = (uv)’dx = (u’v + v’u)dx = vdu + udv
3) d(Cu) = Cdu
4) 
