АНАЛИЗ
Множества чисел
| N |
| ||
| Z | {0, ±1, ±2, ±3,...} Множество целых чисел.Множество целых чисел включает в себя множество натуральных. | ||
| Q | Множество рациональных чисел.Кроме целых чисел имеются ещё и дроби. Дробь — это выражение вида 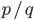 , где p — целое число, q — натуральное. Десятичные дроби также можно записать в виде , где p — целое число, q — натуральное. Десятичные дроби также можно записать в виде 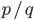 . Например: 0,25 = 25/100 = 1/4. Целые числа также можно записать в виде . Например: 0,25 = 25/100 = 1/4. Целые числа также можно записать в виде 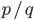 . Например, в виде дроби со знаменателем "один": 2 = 2/1.Таким образом любое рациональное число можно записать десятичной дробью — конечно или бесконечной периодической. . Например, в виде дроби со знаменателем "один": 2 = 2/1.Таким образом любое рациональное число можно записать десятичной дробью — конечно или бесконечной периодической.
| ||
| R | Множество всех вещественных чисел.
Иррациональные числа — это бесконечные непериодические дроби. К ним относятся:
|
Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.
Квантор существования
∃- квантор существования, используется вместо слов "существует",
"имеется". Используется также сочетание символов ∃!, которое читается как существует единственный.
Абсолютная величина
Определение. Абсолютной величиной (модулем) действительного числа  называется неотрицательное число
называется неотрицательное число  , которое определяется по формуле:
, которое определяется по формуле:

Так, например,

Свойства модуля
Если  и
и  – действительные числа, то справедливы равенства:
– действительные числа, то справедливы равенства:

| |

| |

|
Кроме того, справедливо соотношение:

В то же время справедливы неравенства:
 (неравенство треугольника) (неравенство треугольника)
| |

| |

| |

|
Функция
зависимость между двумя или большим количеством величин, при которой каждым значениям одних величин, называемых аргументами функции, ставятся в соответствие значения других величин, называемых значениями функции.
Область определения функции
Областью определения функции называют те значения независимой переменной x, при которых все операции, входящие в функцию будут выполнимы.
Непрерывная функция
Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если

|
Числовые последовательности
функция вида y = f (x), x О N,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f (n)или y 1, y 2,…, yn,…. Значения y 1, y 2, y 3,…называют соответственно первым, вторым, третьим, … членами последовательности.
Предел функции непрерывного аргумента
Число А называется пределом функции y=f(x) при x->x0,если для всех значений x, достаточно мало отличающихся от числа x0, соответствующие значения функции f(x) как угодно мало отличается от числа A
Бесконечно малая функция
Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если  или
или 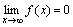 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

|





 — отношение длины окружности к её диаметру;
— отношение длины окружности к её диаметру; — названное в честь Эйлера и др.;
— названное в честь Эйлера и др.;
