Выше говорилось, что если и выполняются условия существования первообразной, то не всегда она может быть найдена как конечная комбинация элементарных функций. Соответствующий интеграл можно рассматривать как новую неэлементарную функцию. Такие функции часто носят название специальных, многие из них хорошо изучены (и табулированы). Например, та из первообразных 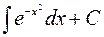 , которая обращается в нуль при х = 0 называется функцией Гаусса и обозначается Ф(х), т.е. Ф(х) =
, которая обращается в нуль при х = 0 называется функцией Гаусса и обозначается Ф(х), т.е. Ф(х) =  если Ф(0) = 0. (Представление о том, как с помощью элементарных функций можно представить и вычислить «неберущиеся» интегралы можно будет получить в разделе 10. «Ряды»).
если Ф(0) = 0. (Представление о том, как с помощью элементарных функций можно представить и вычислить «неберущиеся» интегралы можно будет получить в разделе 10. «Ряды»).
Тесты
3.1.  =
=
1) f (x) + c; 2) f (x) - c; 3) f (x);
3.2. 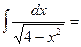
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
3.3. 
1)  ; 2)
; 2) 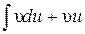 ; 3)
; 3)  .
.
3.4. 
1) 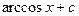 ; 3)
; 3)  ;
;
2)  ; 4)
; 4)  .
.
3.5. 
1)  ;
;
2) 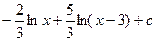 ;
;
3)  .
.
3.6. Простейшей рациональной дробью третьего типа является:
1)  ; 3)
; 3)  ;
;
2) 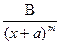 , т = 2, 3, 4…; 4)
, т = 2, 3, 4…; 4)  ,
, 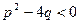 .
.
3.7. 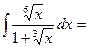
1)  ;
;
2)  ;
;
3)  .
.
3.8. 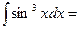
1) 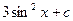 ; 3)
; 3)  ;
;
2)  ; 4)
; 4) 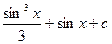 .
.
3.9. 
1) 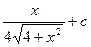 ; 2)
; 2)  ; 3)
; 3) 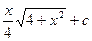 ; 4)
; 4) 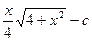 .
.
Ответы к тестам.
1.1. 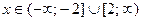 ;
;
1.2.  ;
;
1.3. 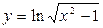 ;
;
1.4.  ;
;
1.5.  ;
;
1.6.  и
и  ;
;
1.7.  ;
;
1.8. Испытывает разрыв 1го рода;
1.9. Пересекает ось Х хотя бы один раз;
1.10. Может быть дифференцируема;
1.11. Непрерывна;
1.12.  ;
;
1.13.  ;
;
1.14.  ;
;
1.15. 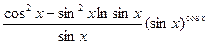 ;
;
1.16. 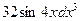 ;
;
1.17. Да: x = 4;
1.18. F ( ; 0);
; 0);
1.19. 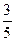 ;
;
1.20. 1;
1.21. (1; -1; 1; -1);
1.22. (-¥; 0);
1.23. (-¥; 0);
1.24. Да. х = 0; (y = 1);
1.25. Да. х = е; (y = e);
1.26. х = 3; (y = 9);
1.27. Да. 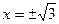 ;
;
1.28. Да. Горизонтально. (х = 0);
2.1. Круг радиуса 2 с центром в начале координат включая границу;
2.2. Эллипсы;
2.3. 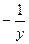 ;
;
2.4. 0;
2.5. 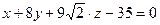 ;
;
2.6.  ;
;
2.7. 1,4;
2.8. 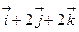 ;
;
2.9. Да. max; (0; 0);
2.10. Имеет min;
3.1. f (x) + c;
3.2.  ;
;
3.3.  ;
;
3.4.  ;
;
3.5.  ;
;
3.6.  ,
, 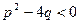 ;
;
3.7.  ;
;
3.8.  ;
;
3.9. 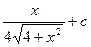 .
.
Литература.
а) Основная:
1. Пискунов Н.С. Дифференциальное и интегральное исчисления (в двух томах) – М.: 1985.
2. Гмурман В.Е. Теория вероятностей и математическая статистика – М:, 1987.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике – М.: 1979, 1997.
4. Данко П.Е., Попов А.Г., Кожевникова Г.Я. Высшая математика в упражнениях и задачах (в двух частях) – М.: 1986, 1996, 1997.
5. Шипачев В.С. Высшая математика, М., Высшая школа, 1995.
6. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Учебник в трех частях- М. Финансы и статистика, 1998.
7. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление, М. Наука, 1988.
8. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. ФКП. М. Наука, 1985.
б) Дополнительная:
9. Минорский В.П. Сборник задач по высшей математике. М. Наука, 1964-1971
10. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. М. ИНФА-М, 1997.
11. Баврин И.И. Курс высшей математики, М. Просвещение, 1992.
12. Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах, М. Издательство МАИ, 2000.
13. Шипачев В.С. Основы высшей математики, М. Высшая школа, 2001.
Содержание
| математический анализ. | |
| Часть 1 | |
| 1. Дифференциальное исчисление функции одной переменной. | |
| 2. Функции нескольких переменных. | |
| 3. Интегральное исчисление | |
| 3.1.Неопределенный интеграл. | |
| Ответы к тестам | |
| Литература | |
| Часть 2 | |
| 3.2. Определенный интеграл | |
| 3.3. Двойной и тройной интегралы | |
| 3.4. Криволинейный интеграл. | |
| 4. Обыкновенные дифференциальные уравнения. | |
| 5. Ряды | |
| 5.1. Числовые ряды | |
| 5.2. Функциональные ряды | |
| Ответы к тестам | |
| Итоговые тесты | |
| Литература |
Гофман Виктор Гершонович
Математический анализ
Учебно-практическое пособие
Подписано к печати:
Тираж:
Заказ №






