Приведем (без доказательств) несколько теорем, утверждения которых играют большую роль в аппарате дифференциального исчисления.
1. Теорема Ролля о корнях производной. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в интервале (а, b) и f(a) = f(b), то в интервале (а, b) найдется хотя бы одно значение х = x, при котором f `( x) = 0. Если f(a) = f(b) = 0 (частный случай), то теорема Ролля означает, что между двумя корнями функции содержится хотя бы один корень ее производной. Геометрическое истолкование: если непрерывная на отрезке [a, b] кривая имеет в каждой точке касательную, не параллельную оси Оу, и равные ординаты в точках а и b, то найдется по крайней мере одна точка x (a < x < b) такая, в которой касательная к кривой параллельна оси Ох (tg a = f `(x) = 0).
2. Теорема Лагранжа (о конечных приращениях): Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b), то в этом интервале найдется хотя бы одно значение х = x, при котором выполяется равенство f(b) – f(a) = (b – a) f `( x).
Геометрический смысл: на дуге АВ непрерывной кривой у = f(x) имеющей в каждой точке касательную не параллельную оси Оу найдется хотя бы одна точка x (a < x < b) такая, в которой касательная параллельна хорде АВ.
3. Теорема Коши (об отношении приращений двух функций): Если функции f(x) и j(x) непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b), причем j`(x) ¹ 0, то в этом интервале найдется хотя бы одно значение х = x (a < x < b) такое, что  . Теорема Коши позволяет доказать два важных для решения задач теории пределов утверждения, известных под названием правила Лопиталя.
. Теорема Коши позволяет доказать два важных для решения задач теории пределов утверждения, известных под названием правила Лопиталя.
Теорема 1. Пусть функции f(x) и j(x) на некотором отрезке [a, b] удовлетворяют условиям теоремы Коши и обращаются в нуль точке а т.е.
f(a) = j(a) = 0; тогда, если существует  , то существует и
, то существует и  , причем
, причем  . Это правило позволяет во многих случаях раскрыть неопределенности вида 0/0 (такие, например, как первый замечательный предел), причем: а) теорема справедлива и в случае, когда f(x) и j(x) неопределены при х = а, но
. Это правило позволяет во многих случаях раскрыть неопределенности вида 0/0 (такие, например, как первый замечательный предел), причем: а) теорема справедлива и в случае, когда f(x) и j(x) неопределены при х = а, но  и
и 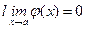 ; б) если f `(a) = j`(a) = 0, а функции f `(x) и j`(x) удовлетворяют условиям теоремы Коши, то, применяя правило Лопиталя дважды, получим
; б) если f `(a) = j`(a) = 0, а функции f `(x) и j`(x) удовлетворяют условиям теоремы Коши, то, применяя правило Лопиталя дважды, получим  ; в) процедура (при выполнении соответствующих условий) может быть повторяема до получения результата.
; в) процедура (при выполнении соответствующих условий) может быть повторяема до получения результата.
Правило справедливо и в случае 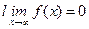 и
и  .
.
Теорема 2. Пусть функции f(x) и j(x) удовлетворяют условиям теоремы Коши при всех х ¹ а в окресности точки а,  и
и  , и пусть существует предел
, и пусть существует предел  . Тогда существует и предел
. Тогда существует и предел  , причем
, причем
 (3.28).
(3.28).
Это правило позволяет раскрывать неопределенности вида  . Оно справедливо и в случаях: а) А = ¥; б) х ® ¥.
. Оно справедливо и в случаях: а) А = ¥; б) х ® ¥.
Во многих случаях это правило позволяет раскрыть неопределенности и других видов, применив предварительно те или иные преобразования. Так, неопределенности вида 0 × ¥ или ¥ – ¥ приводят к виду  или
или  путем алгебраических преобразований данной функции; в случае неопределенности вида 00, ¥0, или 1¥ следует прологарифмировать данную функцию и найти предел ее логарифма.
путем алгебраических преобразований данной функции; в случае неопределенности вида 00, ¥0, или 1¥ следует прологарифмировать данную функцию и найти предел ее логарифма.
Примеры: 1. Неопределенность вида (∞-∞): 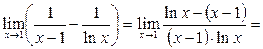 (неопределенность вида
(неопределенность вида  , применяем правило Лопиталя). =
, применяем правило Лопиталя). =  (
( ;правило Лопиталя) =
;правило Лопиталя) = 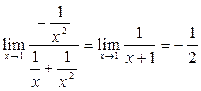
2. Неопределенность вида 00:  . Обозначим
. Обозначим  . Прологарифмируем обе части равенства
. Прологарифмируем обе части равенства 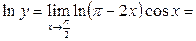 (неопределенность вида ∞·0) =
(неопределенность вида ∞·0) =  (
( ; правило Лопиталя) =
; правило Лопиталя) =  (
( ; правило Лопиталя) =
; правило Лопиталя) =  ;
;  ;
; 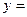 ℮0=1 т.е.
℮0=1 т.е. 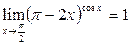 ;
;
Формула Тейлора. Нередко вычисление значений функции y = f(x) при конкретных значениях х оказывается затруднительным. Один из эффективных приемов в этом случае – замена функции степенным многочленом (полиномом) вида: Pn(x – a) = C0 + C1(x – a) + C2(x – a)2 + … + Cn(x – a)n (1) значение которого при х = а равно значению функции f(а). Если функция y = f(x) дифференцируема (n + 1) раз в некоторой окрестности точки а, то коэффициенты Сi можно определить так: потребуем, чтобы в точке а выполнялись условия  , т.е. чтобы в точке а были равны значения соответствующих производных. Получим:
, т.е. чтобы в точке а были равны значения соответствующих производных. Получим:
f(а)= C0; f `(a) = C1; f ``(a) = 2C2 = C2 ×2! ……; f(n)(a) = Cn × n!
где n! = n(n –2)(n –3) … (n – k) … 3 × 2 × 1 (символ n! называется n – факториал). Отсюда легко находятся все  (3.29).
(3.29).
Подставив в (1) получим: 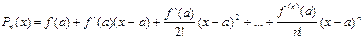 (3.30)
(3.30)
Очевидно, что совпадая при х = а, в других точках значения f(х) и Рn(x) отличаются. Обозначив это отличие через Rn(x) = f(x) – Pn(x) получим:
 (3.31)
(3.31)
Величину Rn(x) называют остаточным членом. Для значений х, при которых остаточный член мал, многочлен Рn(x) дает приближенное значение f(x). Оценить величину Rn(x) при различных х позволяет выражение
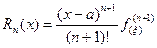 , где a < x < x (3.32).
, где a < x < x (3.32).
(Форма Лагранжа для остаточного члена). Величину x можно представить в виде: x = а + q(х – а), где 0 < q < 1 и тогда (3.32) примет вид
 (3.32`)
(3.32`)
(Очевидно, что, если х расположено в достаточно малой окрестности а. величина Rn при достаточно большом n может быть достаточно мала, чтобы обеспечить требуемую точность).
Выражение (3.31), называется формулой Тейлора. Частный случай ее при а = 0  (3.31`)
(3.31`)
где 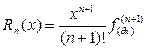 , 0 < q < 1 называется формулой Маклорена. Используя правила дифференцирования, несложно получить разложения многих функций по формуле Маклорена. Приведем некоторые из них:
, 0 < q < 1 называется формулой Маклорена. Используя правила дифференцирования, несложно получить разложения многих функций по формуле Маклорена. Приведем некоторые из них:
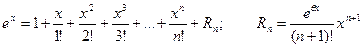 (3.33)
(3.33)
 (3.34)
(3.34)
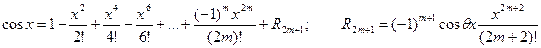 (3.35)
(3.35)
Формула Тейлора может быть применена и для раскрытия неопределенностей вида  и
и  . Функции в числителе и знаменателе дроби «раскладываются» по формуле Тейлора и, после некоторых преобразований, предел вычисляется.
. Функции в числителе и знаменателе дроби «раскладываются» по формуле Тейлора и, после некоторых преобразований, предел вычисляется.
|
 (с учетом соотношений (3.34) и (3.35)) =
(с учетом соотношений (3.34) и (3.35)) = 
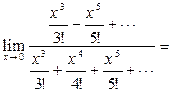


Тесты
1.17. Выполняется ли теорема Ролля для функции  , если а = 0, в = 8? Если да, то при каком значении x?
, если а = 0, в = 8? Если да, то при каком значении x?
1) Да: x = 2; 3) Да: x = 4;
2) Нет; 4) Да: x = 6.
1.18. В какой точке дуги АВ кривой  касательная параллельна хорде АВ, если А(0; 0), В(3; 18)?
касательная параллельна хорде АВ, если А(0; 0), В(3; 18)?
1) С (3; 1); 2) D(2;  ); 3) Е (0;
); 3) Е (0;  ); 4) F (
); 4) F ( ; 0).
; 0).
1.19.  используя правило Лапиталя получим у =
используя правило Лапиталя получим у =
1)  ; 2)
; 2) 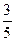 ; 3)
; 3)  ; 4)
; 4)  .
.
1.20.  преобразовав и используя правило Лапиталя получим у =
преобразовав и используя правило Лапиталя получим у =
1) –1; 2) 2; 3) –2; 4) 1.
1.21. Функция  представлена многочленом вида
представлена многочленом вида

 , где
, где  и
и 
1) (1; 2; 3; 4); 2) (1; -1; 1; -1); 3) (1; -2; 3; -4); 4) (-1; 1; -1; 1).






