5. Выяснить, является ли функция возрастающей (убывающей) и найти области возрастания (убывания) функции можно, используя теоремы:
Если функция f(x), имеющая производную на отрезке [a, b] возрастает на этом отрезке, то ее производная на отрезке [a, b] неотрицательна, т.е. f `(x) ³ 0.
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b), причем f `(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].
Если f(x) убывает на отрезке [a, b], то f `(x) £ 0 на этом отрезке.
Если f `(x) < 0 в интервале (a, b), то f(x) убывает на отрезке [a, b].
Полагаем, что f(x) непрерывна на [a, b] и дифференцируема на (a, b).
Геометрическая интерпретация: если функция возрастает, то касательная к ее графику образует острый угол с осью Ох; если функция убывает – угол наклона касательной – тупой.
5. Экстремумы. Говорят, что функция f(x) имеет максимум (max) в точке х0, если значение функции в этой точке больше, чем значения во всех точках малой окресности ее, т.е. если при достаточно малом h > 0 выполняются неравенства: f(x0 – h) < f(x0) и f(x0 + h) < f(x0).
Функция f(x) имеет минимум (min ) в точке х0, если значение функции в этой точке меньше, чем значения во всех точках малой окрестности ее, т.е. если при достаточно малом h > 0 выполняются неравенства:
f(x0 – h) > f(x0) и f(x0 + h) > f(x0).
Максимум (минимум) функции называется ее экстремумом. Точки максимума (минимума) – точками экстремума функции.
Рассмотрим метод отыскания экстремумов.
Необходимое условие существования экстремума можно сформулировать так: Если функция f(x) в точке х0 имеет экстремум, то производная f `(x0) обращается в нуль или не существует.
Это означает, что функция может иметь экстремум только в этих точках, но может и не иметь его в них. Точки эти (в которых производная равна нулю или не существует) называются критическими точками первого рода.
Достаточное условие экстремума можно сформулировать так:
Если х0 – критическая точка функции f(x) и при произвольном достаточно малом h > 0 выполняется неравенство f `(x0 – h) > 0, f `(x0 + h) < 0, то функция f(x) имеет в точке х0 максимум; если f `(x0 – h) < 0, a f `(x0 + h) > 0, то функция f(x) в точке х0 имеет минимум. (Если знаки f `(x0 – h) и f `(x0 + h) одинаковы, то функция f(x) в точке х0 экстремума не имеет). (Наличие экстремума можно определить и с помощью второй производной. Если  , a
, a  то
то  в точке
в точке  имеет экстремум- max, если
имеет экстремум- max, если  и min, если
и min, если  .)
.)
Отметим, что: а) функция, определенная на отрезке, может достигать экстремума только во внутренних точках этого отрезка; б) экстремум функции не обязательно является наибольшим (наименьшим) значением функции на рассматриваемом отрезке.
5. Наибольшее и наименьшее значения функции, непрерывной на отрезке [a, b] можно отыскать, выбрав их из значений функции на концах и в критических точках внутри этого отрезка.
4. Выпуклость и вогнутость графика функции.
 Говорят, что кривая y = f(x) выпукла на интервале (a, b), если все точки ее лежат ниже любой ее касательной, проведенной на этом интервале, (вогнутой – если все ее точки лежат выше любой касательной, проведенной на этом интервале). Условия выпуклости (вогнутости) графика функции на интервале (a, b) можно сформулировать так: Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f ``(x) < 0, то кривая y = f(x) на этом интервале выпукла; если вторая производная положительна, т.е f ``(x) > 0 – кривая вогнута.
Говорят, что кривая y = f(x) выпукла на интервале (a, b), если все точки ее лежат ниже любой ее касательной, проведенной на этом интервале, (вогнутой – если все ее точки лежат выше любой касательной, проведенной на этом интервале). Условия выпуклости (вогнутости) графика функции на интервале (a, b) можно сформулировать так: Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f ``(x) < 0, то кривая y = f(x) на этом интервале выпукла; если вторая производная положительна, т.е f ``(x) > 0 – кривая вогнута.
Выпуклость и вогнутость графика функции наглядно иллюстрируются удобным для запоминания “ правилом дождя ”, поясняемым рис. 3.3. Заключается оно в следующем: если вторая производная отрицательна, то говорят, что “ нет дождя ” – случай а) на рисунке, кривая y1 = f1(x) – выпукла, «струи дождя» скатываются с выпуклой кровли и под ней сухо.
|
Точка, отделяющая вогнутую часть графика от выпуклой, называется точкой перегиба. Можно доказать справедливость утверждения: Если f ``(а) = 0 или f ``(a) не существует и при переходе через значение х = а, f ``(x) меняет знак, то точка кривой y = f(x) с абсциссой х = а есть точка перегиба.
В этой формуле объединены необходимое (равенство нулю или «несуществование» второй производной в некоторой точке) и достаточное (перемена знака второй производной) условия наличия точки перегиба.
Точки, в которых выполняются указанные необходимые условия, называются критическими точками второго рода.
Отметим, что интервалы выпуклости и вогнутости могут быть разделены и точкой разрыва функции, не являющейся точкой перегиба.
5. Асимптоты. Прямая L называется асимптотой кривой y = f(x), если расстояние точки М(х, у) кривой от прямой L стремится к нулю при неограниченном удалении этой точки по кривой от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности).
 Прямая х = а является вертикальной асимптотой кривой y = f(x), если
Прямая х = а является вертикальной асимптотой кривой y = f(x), если  или
или  (подразумевается, что исследуются и левый и правый пределы, т.е.
(подразумевается, что исследуются и левый и правый пределы, т.е.  и
и  ).
).
Прямая у = b является горизонтальной асимптотой кривой y = f(x), если существует предел  или
или  .
.
|
 . Из треугольника MNP определим
. Из треугольника MNP определим  . Т.к. j = arctg к – постоянная,
. Т.к. j = arctg к – постоянная,
то  и
и 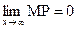 . Но NM = |y – `y| = |f(x) –
. Но NM = |y – `y| = |f(x) –  . При постоянном b
. При постоянном b  , и, следовательно,
, и, следовательно,  , откуда
, откуда  . Зная k находим b:
. Зная k находим b:  . Т.о. прямая y = kx + b является наклонной асимптотой кривой y = f(x), если существуют пределы
. Т.о. прямая y = kx + b является наклонной асимптотой кривой y = f(x), если существуют пределы  (3.36) и
(3.36) и  (3.37)
(3.37)
или  (3.36`) и
(3.36`) и  (3.37`).
(3.37`).
(Если хотя бы один из каждых двух пределов не существует, то кривая наклонных асимптот не имеет).
Рекомендуемая схема построения графиков по характерным точкам:
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Найти точки пересечения графика функции с осями координат.
4. Исследовать функцию на непрерывность, найти (если они существуют) точки разрыва и установить характер разрыва; найти асимптоты кривой.
5. Найти интервалы возрастания и убывания функции и ее экстремумы.
6. Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.
Отметим, что иногда порядок исследования целесообразно выбирать, исходя из особенностей функции. Может быть пополнен и перечень исследуемых характеристик (например вопросом о периодичности функции).
Тесты
1.22. Функция  возрастает на интервале:
возрастает на интервале:
1) (0; ¥); 2) (-¥; 0) и (0; ¥); 3) (-¥; 0); 4) (-3; 3).
1.23. Функция  убывает на:
убывает на:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
1.24 Имеет ли функция  экстремум и, если да, то в каких точках?
экстремум и, если да, то в каких точках?
1) х = ±2; 2) х = 0; 3) х = ± е; 4) х = -8.
1.25. Имеет ли функция  экстремум и, если да, то в каких точках?
экстремум и, если да, то в каких точках?
1) х = 0; 2) х = е; 3) х = 1; 4) х = е -1.
1.26. Функция  на отрезке [0; 3] наибольшее значение принимает в точке:
на отрезке [0; 3] наибольшее значение принимает в точке:
1) х = -1; 2) х = 0; 3) х = 1; 4) х = 3.
1.27. 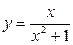 ; Имеет ли график точки перегиба и, если да, то:
; Имеет ли график точки перегиба и, если да, то:
1)  ; 2)
; 2) 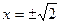 ; 3)
; 3)  ; 4)
; 4) 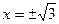 .
.
1.28. 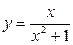 ; Имеет ли график этой функции асимптоты и, если да, то:
; Имеет ли график этой функции асимптоты и, если да, то:
1) Вертикальную;
2) Горизонтальную;
3) наклонную.






