1. Предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных, т.е.
lim (u1 + u2 + … + un) = lim u1+ lim u2+ … + lim un
2. Предел произведения определенного числа переменнных равен произведению пределов этих переменных, т.е.
lim (u1 × u2 × … × un) = lim u1 × lim u2 × … × lim un
3. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля, т.е.  если lim V ¹ 0.
если lim V ¹ 0.
4. Если для соответствующих значений функций u = u(x), z = z(x), v = v(x) выполняются неравенства u £ z £ v и при этом u(x) и v(x) при х ® а (или х ® ¥ ) стремятся к одному и тому же пределу b, то z = z(x) при х ® а (или х ® ¥) стремится к тому же пределу.
Теорема 4 позволяет доказать справедливость важного соотношения, называемого первым замечательным пределом.  (2.1)
(2.1)
Из (2.1) следует эквивалентность бесконечно малых х и sin x: sin x ~x.
 Удобно пояснить это графически. На рис. 2.3 приведены графики функций у = х и у = sinх. Легко видеть, что чем меньше х отличается от нуля, тем меньше отличие ординат (значений функций) соответствующих графиков, а при х = 0 они совпадают. (Это позволяет с высокой точностью при очень малых х определять приближенное значение sin x).
Удобно пояснить это графически. На рис. 2.3 приведены графики функций у = х и у = sinх. Легко видеть, что чем меньше х отличается от нуля, тем меньше отличие ординат (значений функций) соответствующих графиков, а при х = 0 они совпадают. (Это позволяет с высокой точностью при очень малых х определять приближенное значение sin x).
Еще одно важное соотношение теории пределов, называемое вторым замечательным пределом имеет вид:  (2.2)
(2.2)
Число е – иррациональное (также как и число p) и может быть записано в виде бесконечной десятичной непериодической дроби е = 2,71828…; играет важную роль в вычислительной математике, служа, в частности, основанием натурального логарифма, обозначаемого ln x = logex. Функцию у = ех называют экспоненциальной функцией (иногда обозначается как ехр х). В решении задач теории пределов могут быть полезны следующие равенства: 

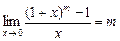 . Можно также заменять бесконечно малые
. Можно также заменять бесконечно малые
величины эквивалентными им: 
Непрерывность функций. Функцию у = f(х) называют непрерывной в точке а если:
1.Эта функция определена в некоторой окрестности точки а и в самой точке;
2.Существует предел функции  и он равен значению функции в этой точке, т.е.
и он равен значению функции в этой точке, т.е.  . Можно предложить и иное определение. Пусть аргумент х0 получит приращение Dх и примет значение х = х0 + Dх. В общем случае функция также получит некоторое приращение Dу = f(х0 + Dх) – f(х0).
. Можно предложить и иное определение. Пусть аргумент х0 получит приращение Dх и примет значение х = х0 + Dх. В общем случае функция также получит некоторое приращение Dу = f(х0 + Dх) – f(х0).
Функцию f(х) называют непрерывной в точке х0, если она определена в этой точке и некоторой окрестности ее и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
 (2.3) или
(2.3) или  (2.3`)
(2.3`)
Приведем формулировку теоремы: Всякая элементарная функция непрерывна в каждой точке, в которой она определена и получим важное для решения задач теории пределов следствие. Запишем условие непрерывности в виде  или, что тоже самое,
или, что тоже самое, 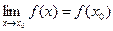 . Но
. Но  и, следовательно,
и, следовательно,  (2.4), т.е. для любой непрерывной функции во всех точках области определения ее справедливо соотношение (2.4) – предел функции равен функции предела (символы (и соответствующие операции) предела и функции можно поменять местами):
(2.4), т.е. для любой непрерывной функции во всех точках области определения ее справедливо соотношение (2.4) – предел функции равен функции предела (символы (и соответствующие операции) предела и функции можно поменять местами):  .
.
Пример: 
В ряде случаев удобно использовать следующее соотношение:
 .
.
Говорят, что если функция f(x) непрерывна в каждой точке некоторого интервала (а, b), где a < b, то функция непрерывна на этом интервале. Точка внутри или на границе области определения, в которой нарушается условие непрерывности, называется точкой разрыва. Если существуют конечные пределы  и
и  , причем не все три числа b1, b2 и f(a) равны между собой, точка а называется точкой разрыва первого рода. Эти точки подразделяются на точки скачка, когда b1 ¹ b2 (скачок равен b2 - b1) и точки устранимого разрыва, когда b1 = b2. Точки разрыва, не являющиеся точками разрыва первого рода, называются точками разрыва второго рода. В этих точках не существует хотя бы один из односторонних пределов (Пример – “бесконечный” разрыв:
, причем не все три числа b1, b2 и f(a) равны между собой, точка а называется точкой разрыва первого рода. Эти точки подразделяются на точки скачка, когда b1 ¹ b2 (скачок равен b2 - b1) и точки устранимого разрыва, когда b1 = b2. Точки разрыва, не являющиеся точками разрыва первого рода, называются точками разрыва второго рода. В этих точках не существует хотя бы один из односторонних пределов (Пример – “бесконечный” разрыв:  ).
).
Рассмотрим некоторые свойства непрерывных функций (доказательства теорем можно найти в рекомендуемой литературе).
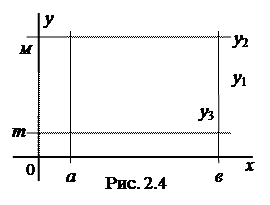
1. Если функция f(x) непрерывна на некотором отрезке [a, b], то на этом отрезке найдется по крайней мере одна точка х = х1 такая, что значение функции в этой точке будет удовлетворять соотношению f(x1) ³ f(x), где х – любая другая точка отрезка, и найдется по крайней мере одна точка х2 такая, что значение функции в этой точке будет удовлетворять соотношению
|
(Отметим, что на интервале (а, b) утверждение теоремы может оказаться неверным. Пример: у = х – функция не имеет на интервале (а, b) наибольшего и наименьшего значений, т.к. не достигает значений а и b!)

|
3. Если функция f(x) определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает неравные значения f(a) = A и f(b) = B то, каково бы ни было число m, заключенное между числами А и В, найдется такая точка х = с, заключенная между a и b, что f(c) = m (легко видеть, что теорема 2 является частным случаем теоремы 3).
Следствие: Если функция f(x) непрерывна на некотором интервале и принимает на нем наибольшее и наименьшее значения, то на этом интервале она принимает по крайней мере один раз любое значение, заключенное между ее наибольшим и наименьшим значениями.
Тесты
1.4. Функция  является бесконечно большой при:
является бесконечно большой при:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
1.5. Функция 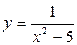 является бесконечно малой при:
является бесконечно малой при:
1)  ; 2)
; 2) 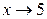 ; 3)
; 3)  ; 4)
; 4)  .
.
1.6. Эквивалентными (бесконечно малыми) при  будут:
будут:
1)  и
и  ; 3)
; 3)  и
и 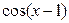 ;
;
2)  и
и  ; 4)
; 4)  и
и  .
.
1.7. Какой из пределов называют «вторым замечательным»:
1)  ; 3)
; 3)  ;
;
2)  ; 4)
; 4)  .
.
1.8. Функция  в точке х = -1:
в точке х = -1:
1) Непрерывна;
2) Испытывает разрыв 2го рода;
3) Испытывает разрыв 1го рода.
1.9. Если непрерывная функция на концах отрезка [ а; в ] принимает значения разного знака, то ее график:
1) пересекает ось Х один раз;
2) не пересекает ось Х;
3) пересекает ось Х хотя бы один раз.
Производная.
Рассмотрим функцию у = f(x) определенную на некотором интервале. Дадим аргументу х приращение Dх. Новому значению аргумента х + Dх будет, в общем случае, соответствовать новое значение функции f (x + Dх), т.е. функция также получит некоторое приращение
Dу = f (x + Dх) – f (x). Составим отношение  . Если
. Если 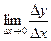 существует, то его называют производной данной функции и обозначают y` (или f`(x) или dy / dx). Иногда используют обозначение у`х – индекс показывает, по какому аргументу берется производная.
существует, то его называют производной данной функции и обозначают y` (или f`(x) или dy / dx). Иногда используют обозначение у`х – индекс показывает, по какому аргументу берется производная.
 (3.1) или
(3.1) или  (3.1`)
(3.1`)
Производной данной функции y = f(x) по аргументу х называют предел отношения приращения функции Dу к приращению аргумента Dх, когда последнее произвольным образом стремится к нулю. В общем случае производная также является некоторой функцией от х. (f`(x) = j(x)). Конкретное значение производной при х = а обозначают f `(а) или у`/х = а. Операцию нахождения производной называют дифференцированием функции.
Понятие производной (и соответствующий математический аппарат) широко используются в различных прикладных задачах. Пример: Известно, что средняя скорость движения тела определяется выражением V = s / t (s = s (t) – путь пройденный телом, t время движения). Очевидно, что мгновенную скорость можно найти, как  (механический смысл производной). Рассмотрим геометрическую интерпретацию.
(механический смысл производной). Рассмотрим геометрическую интерпретацию.
|
 Возьмем на графике функции y = f(x) (рис.3.1) произвольные точки М0(х, у) и М1(х + Dх, у + Dу) и проведем секущую М0М1. Очевидно, что угол наклона секущей к оси Ох определяется выражением
Возьмем на графике функции y = f(x) (рис.3.1) произвольные точки М0(х, у) и М1(х + Dх, у + Dу) и проведем секущую М0М1. Очевидно, что угол наклона секущей к оси Ох определяется выражением  . Если точка М1 приближается к точке М0, то секущая поворачивается вокруг точки М0 (при этом Dх ® 0) и в пределе занимает положение касательной к графику функции, проведенной через точку М0.
. Если точка М1 приближается к точке М0, то секущая поворачивается вокруг точки М0 (при этом Dх ® 0) и в пределе занимает положение касательной к графику функции, проведенной через точку М0.
Угол наклона касательной определится выражением  .
.
Геометрический смысл производной очевиден: Значение производной f`(x) при данном значении аргумента х равняется тангенсу угла наклона касательной к графику функции f(x) в соответствующей точке М(х, у). Это, с учетом (1.36), позволяет записать уравнение касательной к кривой у = f(x) в точке (х0, у0) в виде у – у0 = f `(x0)(x – x0) (3.3).
Говорят, что если функция y = f(x) имеет производную в точке х = х0, т.е. если существует предел  , она дифференцируема в этой точке. Если функция дифференцируема в каждой точке некоторого отрезка (интервала), говорят, что она дифференцируема на отрезке (интервале).
, она дифференцируема в этой точке. Если функция дифференцируема в каждой точке некоторого отрезка (интервала), говорят, что она дифференцируема на отрезке (интервале).
Теорема. Если функция у = f(х) дифференцируема в некоторой точке, то она в этой точке непрерывна. Действительно, если  , то
, то  , где g – бесконечно малая величина, т.е.
, где g – бесконечно малая величина, т.е.  . Но тогда Dу = f `(x0) Dx + gDx, откуда следует, что Dу ® 0 при Dх ® 0 и функция f(x) непрерывна в точке х0. Очевидно, в точках разрыва функция не может иметь производной. Это не значит однако, что если функция непрерывна в точке х0, то она дифференцируема в ней. Рассмотрим функцию, график которой представлен
. Но тогда Dу = f `(x0) Dx + gDx, откуда следует, что Dу ® 0 при Dх ® 0 и функция f(x) непрерывна в точке х0. Очевидно, в точках разрыва функция не может иметь производной. Это не значит однако, что если функция непрерывна в точке х0, то она дифференцируема в ней. Рассмотрим функцию, график которой представлен
 на рисунке. Функция непрерывна во всех точках [a, b]. Однако в точке с к графику функции можно провести две различные касательные, т.е. в этой точке первая производная не существует (испытывает разрыв) и функция непрерывна, но не дифференцируема.
на рисунке. Функция непрерывна во всех точках [a, b]. Однако в точке с к графику функции можно провести две различные касательные, т.е. в этой точке первая производная не существует (испытывает разрыв) и функция непрерывна, но не дифференцируема.
Рассмотрим функцию 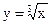 в точке х = 0.
в точке х = 0.  , т.е. в точке х = 0 рассматриваемая функция непрерывна, но не дифференцируема.
, т.е. в точке х = 0 рассматриваемая функция непрерывна, но не дифференцируема.
Рассмотрим производные основных элементарных функций. Пусть у = х2. Очевидно Dу = (x + Dx)2 – х2 = 2xDx + D2 х и  , т.е. если у = х2, то у` = 2х. Рассуждая аналогично, несложно доказать, что производная функции у = хn, где n – целое положительное число, равна nxn–1, т.е. если у = хn, то у` = nхn–1 (3.4). Эта формула, как будет показано ниже, верна и в случае любого действительного n. Приведем без доказательств следующие утверждения:
, т.е. если у = х2, то у` = 2х. Рассуждая аналогично, несложно доказать, что производная функции у = хn, где n – целое положительное число, равна nxn–1, т.е. если у = хn, то у` = nхn–1 (3.4). Эта формула, как будет показано ниже, верна и в случае любого действительного n. Приведем без доказательств следующие утверждения:
Если у = sinx, то y` = cosx (3.5) Если у = cosx, то y` = – sinx (3.6)
Производная постоянной равна нулю, т.е. если у = с, где с – постоянная, то с` = 0 (3.7)
Постоянный множитель можно выносить за знак производной, если у = c f(x), где c = const, то y` = cf `(x) (3.8).
Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций, т.е. если  , то
, то  (3.9)
(3.9)
( – символ суммы индексированных (нумерованных) величин, где i – текущий индекс, к и n – нижний и верхний пределы суммы – т.е. номера первой и последней складываемых величин.)
– символ суммы индексированных (нумерованных) величин, где i – текущий индекс, к и n – нижний и верхний пределы суммы – т.е. номера первой и последней складываемых величин.)
Производная произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную второй, т.е. если у = uv, то
y` = u`v + uv` (3.10).
Производная дроби (частного от деления двух функций) равна дроби, знаменатель которой есть квадрат знаменателя данной дроби, а числитель есть разность произведений производной числителя на знаменатель и производной знаменателя на числитель, т.е. если y = u / v, то  (3.11).
(3.11).
Используя приведенные соотношения можно получить производные других элементарных функций и составить таблицу производных. Приведем их, опуская доказательства.
Если у = logax, то  (3.12). Очевидно,
(3.12). Очевидно,  (3.12`)
(3.12`)
Если y = tg x, то  (3.13) Если y = сtg x, то
(3.13) Если y = сtg x, то 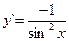 (3.14)
(3.14)
Если у = ах (a > 0), у` = ахln a (3.15) и (ех)` = ex (3.15`)
Рассмотрим особенности нахождения производной от сложной функции - функции вида у = F(u), где u = f(x), или у = F(f(x). Переменную u называют промежуточным аргументом.
Теорема: Если функция u = f(x) имеет в некоторой точке х производную ux` = f `(x), а функция y = F(u), имеет при соответсвующем значении u производную y`u = F(u), то сложная функция у = F(f(x)) в указаной точке х также имеет производную y`х = F`u(u)f `(x) или y`x=y`uu`x (3.16)
(Иначе – производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента).
Пример: y = sin x2 => y = sin u, u = x2, используя (3.16). (3.5) и (3.4) получим: y`u = cos u, u`x = 2x, y`x = 2xcos x2.
Приведенное правило позволяет получить производную неявной функции т.е. функции, заданной уравнением F(x, y) = 0 (3.17).
(Отметим, что если в (3.17) удастся привести уравнение к виду у = f (х), то функция оказывается заданной в явном виде. Операция эта осуществима далеко не всегда).
Пример: F(x, y) = sin (x + y) – e(x – y) = 0. Дифференцируя обе части равенства по х и помня, что у есть функция от х, получим:

В некоторых случаях, прежде чем найти производную, бывает удобно прологарифмировать уравнение, задающее функцию. Пусть у = хn. Прологарифмировав обе части равенства, получим ln y = n ln x, откуда  для произвольного действительного n. Выражение
для произвольного действительного n. Выражение  называют логарифмической производной. (Отметим, что логарифмическое дифференцирование удобно применять при нахождении производных от произведения большого количества функций и показательно-степенных функций).
называют логарифмической производной. (Отметим, что логарифмическое дифференцирование удобно применять при нахождении производных от произведения большого количества функций и показательно-степенных функций).
Найдем производную обратной функции. Пусть y = f(x) возрастающая или убывающая функция, определенная на некотором интервале (a, b), (a < b). (Если большему значению аргумента соответствует большее значение функции (f(x2) > f(x1) при x2 > x1) ее называют возрастающей. Если f(x2) < f(x1) при x2 > x1 функция убывающая). Для определенности (без потери общности) рассмотрим возрастающую функцию. Из определения ее очевидно, что значения х и у связывает взаимно однозначное соответствие. Рассматривая у как аргумент, а х как функцию, свяжем их значения соотношением х = j(у). Эта функция является обратной для функции y = f(x), а функция y = f(x) обратной для х = j(у). Эти функции имеют один и тот же график и функция х = j(у) находится как решение уравнения y = f(x) относительно х. Отметим, что:
1. Если возрастающая (убывающая) функция непрерывна на отрезке [a, b], причем f(a) = c, f(b) = d, то обратная функция определена и непрерывна на отрезке [c, d];
2. Если функция y = f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций (однозначных).
Пример: у = х2 на интервале (–¥, ¥) не является ни возрастающей, ни убывающей и имеет две обратные функции:  (0 £ х < ¥) и
(0 £ х < ¥) и  (- ¥ < х < 0).
(- ¥ < х < 0).
Теорема: Если для функции y = f(x) существует обратная функция х = j(у), которая в рассматриваемой точке у имеет производрую j`(у) отличную от нуля, то в соответствующей точке х функция y = f(x) имеет производную f `(x) равную 1 / j`(у), т.е. справедлива формула
f`(x) = 1 / j`(у) (3.18).
Используя полученное правило, пополним таблицу производных:
Если y = arcsin x, то  (3.19) Если y = arccos x, то
(3.19) Если y = arccos x, то  (3.20)
(3.20)
Если y = arctg x, то  (3.21) Если y = arcctg x, то
(3.21) Если y = arcctg x, то 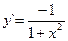 (3.22)
(3.22)
|

 Используя (3.11) найдем:
Используя (3.11) найдем:

(Напомним, что sin2x + cos2x=1; sin2x = 2sinx cosx)
у = хх. Прологарифмировав обе части равенства по основанию е получим lnу = xlnx. Продифференцировав обе части равенства, найдем (lny)` = (xlnx)` => y`/ у = lnx + 1 => y` = xx (lnx + 1).
Выведем фомулу (3.19). Итак, y = arc sin x => sin y = sin arc sin x => x = sin y. Воспользуемся (3.18):

В ряде случаев функциональную зависимость (линию, поверхность) удобно задавать в параметрической форме: каждая неизвестная (координата точки) представляется функцией параметра t, причём каждому значению параметра соответствуют координаты некоторой точки (значения неизвестных, удовлетворяющих обычному уравнению зависимости);  и т.д. (Пример - параметрические уравнения прямой в разделе 1.7.1)
и т.д. (Пример - параметрические уравнения прямой в разделе 1.7.1)
(От параметрического задания функции легко перейти к привычному  , исключив из уравнений параметр t - разрешив уравнение (1) относительно t и подставив его в (2)). Производная функции, заданной параметрически, определяется выражением:
, исключив из уравнений параметр t - разрешив уравнение (1) относительно t и подставив его в (2)). Производная функции, заданной параметрически, определяется выражением: 
Рассмотрим понятие производных высшего порядка. Производную от функции y = f(x) (ее называют первой), обозначаемую y` = f`(x) = dy / dx можно рассматривать как новую (по отношению к f(x)) функцию той же переменной. Эта функция, в свою очередь, может быть продифференцирована, т.е. найдена первая производная от первой производной исходной функции f(x); (y`)`=(f`(x))`. Она называется второй производной, обозначается y`` = f ``(x) = d2y / dx2 и является производной высшего (второго) порядка. Очевидно, что таким же образом может быть определена производная n–го порядка (n Î Z), обозначаемая y(n) = f(n)(x) (n – берется в скобках, чтобы не путать с показателем степени). Иногда порядок производной обозначают римскими цифрами.
Дифференциал.
Если функция y = f(x) дифференцируема на некотором отрезке, то производная  принимает определенные значения. Отношение Dу/Dх при Dх ® 0 можно представить в виде
принимает определенные значения. Отношение Dу/Dх при Dх ® 0 можно представить в виде 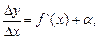 где a ® 0 при Dх ® 0. Умножая равенство на Dх получим Dу = f `(x) Dx + aDx. В общем случае f`(x) ¹ 0 и произведение f `(x) Dх есть величина бесконечно малая одного порядка с Dх, а aDх – бесконечно малая высшего порядка. Первое из двух слагаемых (f`(x) Dх) называют главной частью приращения функции, линейной относительно Dх, или дифференциалом функции и обозначают dy = f `(x) Dх.
где a ® 0 при Dх ® 0. Умножая равенство на Dх получим Dу = f `(x) Dx + aDx. В общем случае f`(x) ¹ 0 и произведение f `(x) Dх есть величина бесконечно малая одного порядка с Dх, а aDх – бесконечно малая высшего порядка. Первое из двух слагаемых (f`(x) Dх) называют главной частью приращения функции, линейной относительно Dх, или дифференциалом функции и обозначают dy = f `(x) Dх.
Пусть у = х. Очевидно, что dy = dx и дифференциал независимого переменного совпадает с приращением и можно записать dy = f`(x)dx (3.24).
Производную функции f`(x) = dy / dx можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
То, что в выражении Dу = dy + aDx второе слагаемое является бесконечно малой более высокого порядка, позволяет в приближенных вычислениях использовать следующий алгоритм:
Dу» f `(х)Dх => f (х+Dх) – f (х) @ f `(x) Dх => f (x + Dх) @ f(x) + f `(x) Dх (3.25.),
причем вычисления тем точнее, чем меньше величина Dх.
Пример: Вычислим приближенное значение sin460; 460 = 450 + 10 = p/4 + p/180; Из (3.25) очевидно, что sin(x + Dх)» sin x + Dх cosx и sin 460 = sin (p/4 + p/180) @ sin p/4 + (p/180)cos p/4» 0,7194.
|
 d(u + v) = du + dv (3.26), d(uv) = vdu + udv (3.27) и т.д.
d(u + v) = du + dv (3.26), d(uv) = vdu + udv (3.27) и т.д.
Геометрический смысл дифференциала легко уяснить из рис. 3.2. Возьмем на кривой у = f(x) произвольную точку М(х, у) и проведем касательную. Приращению Dх аргумента соответствует приращение Dу функции и точка М1(х + Dх, у + Dу). Из треугольника МNT находим NT = MN tg a = Dх f `(x) = dy (по определению дифференциала), т.е. геометрически дифференциал представляет собой приращение ординаты касательной к графику функции в точке М (х,у).
Аналогично тому, как определяются производные высших порядков, определяются и их дифференциалы. Дифференциал от дифференциала называют дифференциалом второго порядка (вторым дифференциалом) и обозначают d(dy) = dy2. По определению дифференциала d2y = [f `(x) dx]`dx = f``(x)(dx)2, так как dx от х не зависит. Очевидно, таким же образом определяется дифференциал любого порядка dny = f(n)(x)(dx)n; принято записывая порядок дифференциала опускать скобки, т.е окончательно общее выражение примет вид
dny = f(n)(x)dxn (3.24').
Тесты
1.10. Если точка в некоторой точке непрерывна, то она в этой точке:
1) Может быть дифференцируема;
2) Дифференцируема;
3) Не дифференцируема.
1.11. Если функция в точке дифференцируема, то она в этой точке:
1) испытывает разрыв;
2) может быть непрерывна;
3) Непрерывна.
1.12. Если  , то у ' =
, то у ' =
1)  ; 2)
; 2) 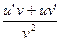 ; 3)
; 3)  .
.
1.13. Если 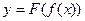 , то у ' =
, то у ' =
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
1.14.  , у ''' =
, у ''' =
1)  ; 3)
; 3)  ;
;
2)  ; 4)
; 4)  .
.
1.15.  ; у ' =
; у ' =
1)  ; 3)
; 3) 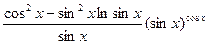 ;
;
2)  ; 4)
; 4)  .
.
1.16.  ; d 3 x =
; d 3 x =
1)  ; 3)
; 3)  ;
;
2)  ; 4)
; 4) 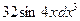 .
.






