ЭЛЛИПТИЧЕСКОГО ТИПА
Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма 
Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:
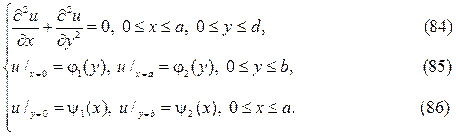
следует искать в виде суммы u (x,y) =v (x,y) +w (x,y),где v (x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач
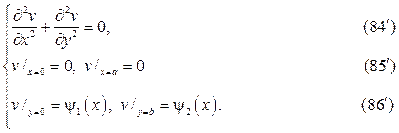
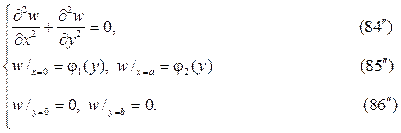
Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.
Рассмотрим задачу Дирихле для круга
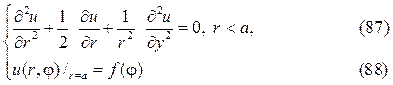
где f (j)кусочно-непрерывная функция.
Следуя схеме метода Фурье полагаем
u (r, j) = R (r) F(j) (89)
подставляем в (87) и разделяем переменные. В результате получим ра -венство
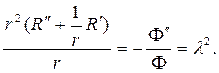(90)
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля
откуда следует, что
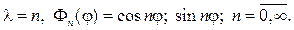(91)
Возвращаясь к (80), решаем уравнение для радианальной функции. При
n ³ 1 имеем
r2R² + rR¢ n2R = 0,
решение следует искать в виде степенной функции R=r m. Для определе- ния m получим соотношение
m(m 1) r m+m r m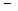 
n 2 r m=0Û m2 
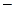n 2=0,
поэтому
m = ± n, Rn (r) = rn; r-n. (92)
Если же n =0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции
R 0(r) = 1; ln r.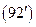 
С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге
1, r cosj, r sin j, …, rn cos n j, rn sin n j, ….
Если предположить, что ряд
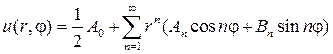(93)
можно дифференцировать почленно дважды по r и j, то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем
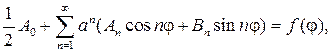(94)
откуда с учетом формул коэффициентов Фурье следует
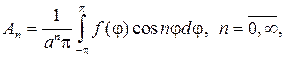(95)
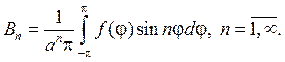(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r < a. При его нахождении мы не привлекали радиальных функций r-n и ln r, поскольку они разрывны в
центре круга r =0.
Напротив, если рассматривать область r > a, то нельзя привлекать r-n и ln r, и общий вид гармонической функции для внешности круга будет да- ваться рядом
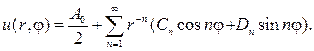(97)
В случае кругового кольца a < r < b необходимо привлекать все встре- тившиеся выше радиальные функции (92 92¢) и гармоническая функция примет вид
Отметим, что соотношения (93), (97 98) позволяют решать также вторую и третью краевые задачи для названных областей.
Замечание 2. В простейших случаях, когда f (j) есть тригонометричес-
кий полином, т.е. линейная комбинация
коэффициенты An и Bn находятся из равенства (94) путем приравнивания коэффициентов возле одноименных функций слева и справа. Решение задачи (87 88) будет на этот раз представлено в виде конечной суммы.
Рассмотрим теперь первую краевую задачу для уравнения Лапласа в шаре радиуса а:
Полагая u (r, j,q) = R (r) Y (j,q), после подстановки в (99) и разделения переменных получим равенство
(101)
которое распадается на два дифференциальных уравнения с неизвестным параметром l.Их нужно решать при условии ограниченности в области изменения переменных 0 £ r £ a, 0 £ q £ p,0 £ j £ 2p, и периодичность по переменной j с периодом 2p так, что Y (j+2p,q)= Y (j,q).
Дифференциальное уравнение
(102)
снова решаем разделением переменных, полагая 
Подставляем в (102) и находим
(103)
Для функции F(j) с учетом периодичности получим уже встретившуюся выше при решении задачи Дирихи для круга задачу Штурма Лиувилля
откуда согласно формуле (91)
m= m, F m (j)=cos m j; sin m j; m = 
.
Тогда второе из уравнений (73) примет вид
(104)
и его нужно решать при условиях ограниченности
(105)
В уравнении (104) изменим независимую переменную, полагая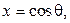 
тогда 
и 
или с
учетом того, что sin2q= 1- x 2, найдем
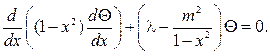(104¢)
Соответственно и граничные условия (105) перейдут после замены в неравенства
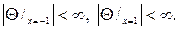(105′)
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)
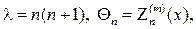
и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):
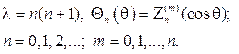(106)
Составив произведения функций (106) на найденные выше функции F m (j), получим множество решений уравнения (102)
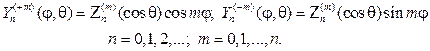(107)
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.
Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m 1¹ m 2 или n 1¹ n 2
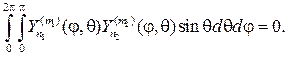(108)
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции
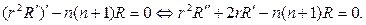
Оно имеет решение в виде степенной функции R=rm. Действительно, после подстановки
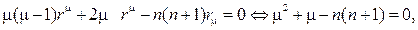
откуда находим значения m= n; (n +1) и соответственно решения
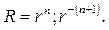(109)
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:
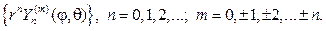
Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами
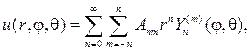(110)
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.
Для нахождения коэффициентов Аnm подставим (110) в (100), тогда
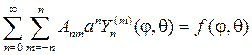
и с учетом (108) найдем
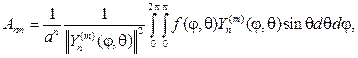(111)
где
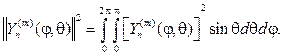
Последний интеграл вычисляется и при m =0:
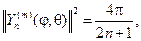(112)
если же | m | ³ 1, то имеем
(113)
Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).
Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам
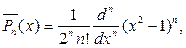(114)
соответственно
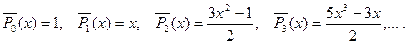
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.
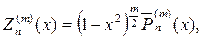(115)
в частности будем иметь
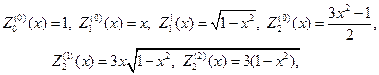
и при любом n
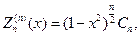(116)
где Сn определенная константа.
С учетом (107), (115) и (116) выпишем несколько сферических функций:
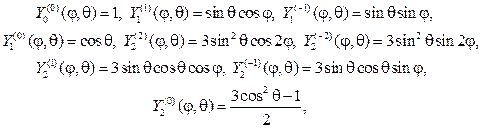
и при любом n
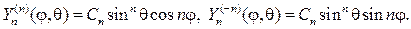(117)
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд
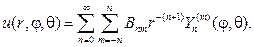(118)
Общий вид гармонической функции в шаровом слое a < r < b получа- ется сложением формул (110) и (118).
Замечание5. При некоторых правых частях удается найти частное ре- шение уравнения Пуассона и свести краевую задачу для уравнения Пуас- сона к краевой задаче для уравнения Лапласа, которая решается методом Фурье.
248. Найдите решение краевой задачи в прямоугольнике
Р е ше н и е. Как и в общем случае, полагая u=v (x,y) +w (x,y), где v (x,y) есть решение задачи
Для ее решения берем v (x,y) =X (x) Y (y), тогда
и мы пришли к задаче Штурма Лиувилля
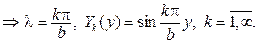
Для функции X (x) будем иметь уравнение 
общее ре-
шение которого может быть записано в виде
Тогда сумма ряда (если его можно дважды дифференцировать почленно)
будет гармонической функцией в прямоугольнике. В силу первого из граничных условий будем иметь
Из второго граничного условия найдем
Подставляя значения найденных коэффициентов в ряд, придем к ра -венству
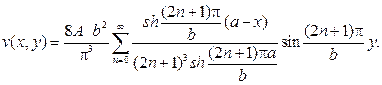
Функция w (x,y) есть решение задачи Дирихле
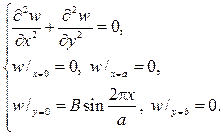
Снова по методу Фурье w (x,y) = X (x) Y (y). На этот раз придем к задаче
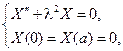
Для функции Y (y)получится дифференциальное уравнение
Перемножая Yj (y) и Xj (x) и суммируя по всем j, найдем гармоничес- кую в прямоугольнике и равную нулю на сторонах х =0 и х = а функцию
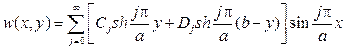
С учетом граничного условия при y =0 имеем
Из граничного условия w/y=b=0 вытекает
Таким образом получаем, что 
Складывая найденные функции v (x,y) и w (x,y), придем к ответу
249. Найдите решение краевой задачи в прямоугольнике
W={(x, y): 0 £ x £ a, 0 £ y £ b }
По методу Фурье полагаем u (x,y) = X (x) Y (y) и приходим к равенству
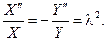
Из граничных условий при y =0и y=b найдем 
Далее из задачи Штурма Лиувилля
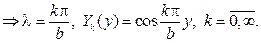
Для функции Х (х) имеем дифференциальное уравнение
Если 
то его общее решение имеет вид
при k =0 общее решение будет линейной функцией Х 0(х)= А 0 х+В 0. Гармо- ническая функция в W
будет, очевидно, удовлетворять условиям 
Остается выбрать ее коэффициенты так, чтобы выполнялись граничные условия на сторонах x =0 и x=a.
Будем иметь
При четных k =2 n коэффициенты A 2 n =0,поэтому окончательно реше-ние запишется в виде
250. Найдите стационарное распределение температуры в прямоугольной пластине 
если стороны х=а и у=b покрыты тепловой изоляцией, стороны х =0 и у =0 поддерживаются при нулевой температуре, и в пластинке выделяется тепло с плотностью Q.
Р е ш е н и е. Текстовая задача равносильна следующей краевой зада- че (k – коэффициент внутренней теплопроводности)
Возьмем частное решение, зависящее только от у
выберем константу С так, чтобы
Полагая теперь 
, придем к краевой задаче для уравнения Лапласа относительного новой неизвестной функции v (x,y):
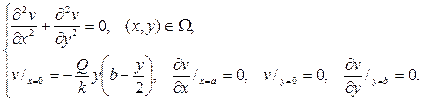
Как обычно, полагаем теперь 
и приходим к диффе- ренциальным уравнениям
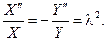
Из граничных условий 
находим, что 
Следовательно, нужно решать задачу Штурма Лиувилля:
Для функции Х (х) будем иметь уравнение 
и его решение может быть записано в виде
Гармоническая в W функция
удовлетворяет условиям 
и остается выбрать коэффи- циенты An и Bn так, чтобы выполнялись два других граничных условия
Подставляя найденные коэффициенты в ряд, найдем
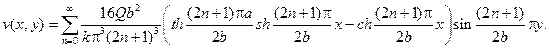
Решение исходной задачи получится окончательно в форме
251. Найдите стационарную температуру u (r,z) внутренних точек ци- линдра 
если температура нижнего основания и боковой поверхности равна нулю, а температура верхнего основания u (r,h) =f (r).
Р е ш е н и е. Здесь нужно решать уравнение Лапласа в W, и поскольку температура не зависит от j, то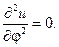 
Стало быть краевая задача запи- шется в форме
и решать ее нужно методом Фурье, полагая u (r,z) =R (r) Z (z). После разде- ления переменных в дифференциальном уравнении получим
Из граничного условия на боковой поверхности u/r=a =0 следует, что R (a)=0, поэтому с учетом обращения в нуль коэффициента k (r)= r при r =0 придем к задаче Штурма Лиувилля:
Собственные функции этой задачи образуют ортогональную систему с весом r на отрезке [0, а ] (см. теорему 2 из параграфа 3). Дифференциальное уравнение
после введения новой переменной 
приводится к уравнению Бес- селя нулевого порядка:
Применяя граничные условия, будем иметь с учетом того, что J 0(0)=1, N 0(0)=¥ и 
положительные нули функции J 0(x):
следовательно
Из дифференциального уравнения
вытекает, что
Составляем ряд
Из условия u/ z=0=0 найдем, что
Из граничного условия на верхнем основании (см. (81))
С учетом найденных значений коэффициентов придем к ответу:
252. Найдите стационарную температуру u (r,z) внутренних точек цилин- дра 
если температура верхнего
основания и боковой поверхности равна нулю, а к нижнему основанию подводится постоянный тепловой поток q.
Р е ш е н и е. Текстовая задача равносильна следующей краевой зада-
че (k – коэффициент теплопроводности) в W
Как и в предыдущей задаче находится гармоническая в W функция, равная нулю на боковой поверхности
здесь вместо линейной комбинации гиперболических синуса и косинуса взята линейная комбинация гиперболического синуса и его сдвига. При- меняя условие u/z=h =0,
Из граничного условия на нижнем основании будем иметь
С учетом значений коэффициентов Аn и Bn придем к ответу
253. Найдите решение краевой задачи
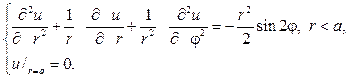
Р е ш е н и е. Сперва найдем частное решение уравнения Пуассона в виде u 0(r, j)= v (r)sin2j.
Тогда
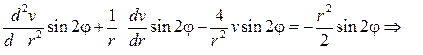
Очевидно, решение уравнения Эйлера нужно искать в виде v=cr 4, и получим
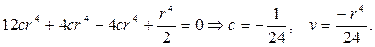
Таким образом, частным решением будет функция
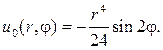
Вводим новую неизвестную функцию w (r,j), полагая
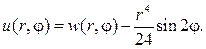
Тогда относительно w (r, j) нужно решать задачу Дирихле для урав- нения Лапласа
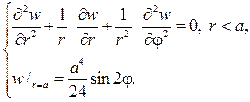
Согласно (93), решение этой задачи дается формулой
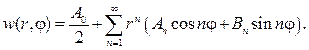
Подставляя ее в граничное условие, получим
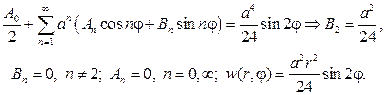
Ответом в задаче будет функция
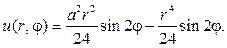
254. Найдите решение первой краевой задачи для уравнения Гельмгольца
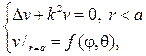
предполагая, что k не является собственным значением задачи
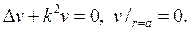
Р е ш е н и е. Запишем уравнение в сферических координатах
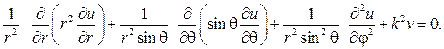
Беря u (r, j,q,)= R (r) Y (j,q), после разделения переменных придем к дифференциальным уравнениям:
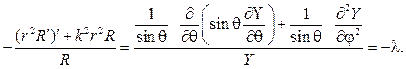
Функция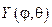 
будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l =n (n +1):
Относительно радиальной функции R (r) нужно решать дифференци- альное уравнение
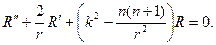
Выполняя в этом уравнении замену
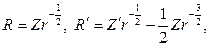
придем к соотношению относительно новой функции Z (r):
Последнее уравнение в качестве ограниченных в окрестности нуля
r= 0 решений имеет бесселевы функции
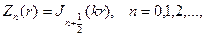
соответственно будем иметь набор радиальных функций
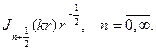
Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:
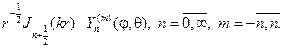
Составляем ряд с числовыми коэффициентами
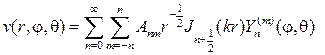(119)
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a
где d = 4 при m = 0 и d =2 при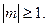 
При найденных коэффициентах Anm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.
255. Найдите такую гармоническую u (r, j,q ) функцию внутри шарового слоя 1 < r < 2, чтобы выполнялись условия
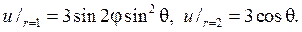
Р е ш е н и е. Согласно (80), (88) и замечанию 4 общий вид гармонической функции в шаровом слое
(120)
Поскольку 
то можно считать в (120) все коэффициенты равными нулю, кроме 
Отмечен- ные четыре коэффициента будут решениями уравнений
В итоге получим, что искомая гармоническая функция в шаровом слое имеет вид
256. Найдите решение краевой задачи в прямоугольнике
257. Найдите стационарное распределение температуры внутри тонкой прямоугольной пластинки 
если к стороне у =0 подводится постоянный тепловой поток q, а остальные три стороны поддерживаются при постоянной температуре u 1.
258. Найдите потенциал электростатического поля u (x,y) внутри прямоу- гольника если вдоль стороны у =0потенци- ал равен u 1, а три другие стороны заземлены. Электрические заряды внут- ри W отсутствуют.
259. Найдите стационарное распределение температуры u (x,y) в прямоу- гольной пластинке если стороны х=а и у=b покрыты тепловой изоляцией, две другие стороны поддерживаются при нулевой температуре, а в пластинке выделяется тепло с постоянной плот- ностью q.
260. Найдите решение уравнения Лапласа в полуполосе удовлетворяющее краевым условиям u (0, y)=0, u (a,y)=0, u (x,0)= A (a x), u (x,¥)=0.
261. Найдите решение уравнения Лапласа в полуполосе удовлетворяющее краевым условиям u (0, y)=0, 
262. Найдите распределение потенциала электростатического поля u (x,y,z) внутри прямоугольного параллелепипеда {0£ x £ a, 0£ y £ b, 0£ z £ c }, если его боковые грани и верхнее основание заземлены, а нижнее основание заряжено до потенциала u 1.
263.Найдите стационарную температуру u (r,z) внутренних точек цилинд- ра радиуса а и высотой h, если температура обоих оснований равна нулю и на боковой поверхности u (r,z)/ r=a=f (z).
264. Найдите стационарное распределение температуры в цилиндре {0£ r £ a, 0£j£2p, 0£ z £ h }, если нижнее основание имеет температуру u1, а на остальной поверхности температура равна нулю.
265. Нижнее основание цилиндра {0£ r £ a, 0£j£2p, 0£ z £ h }, имеет нуле- вую температуру, верхнее теплоизолировано, а температура боковой по- верхности равна 0. Найдите стационарное распределение температуры внутри цилиндра.
Решите следующие краевые задачи
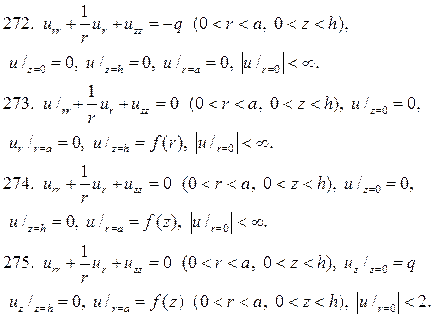
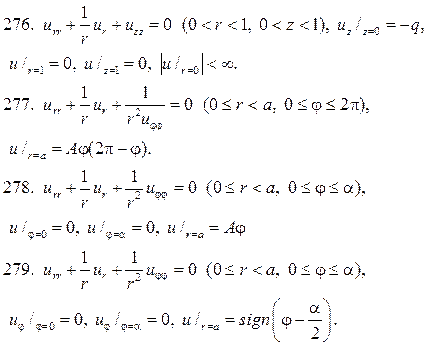
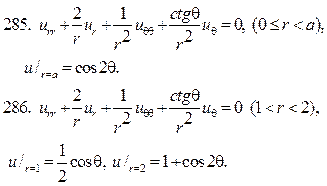
Литература
1. Смирнов В.И. Курс высшей математики. Т. 1 5. М.: Физматгиз, 1958-1960.
2. Ильин В.А., Позняк Э. Г. Основы математического анализа. М.: Наука, 1965.
3. Будак Б.М., Фомин С.В. Кратные интегралы и ряды. М.: Наука, 1965.
4. Свешников А. Г., Тихонов А. Н.Теория функций комплексной переменной. М.: Наука, 1967.
5. Демидович Б. П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1972.
6. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.
7. Арсенин В. Я. Математическая физика.- М.: Наука, 1966.
8. Владимиров В. С. Уравнения математической физики. М.: Наука, 1967.
9. Кошляков Н. С., Глинер Э. Б., Смирнов М. М. Основные дифференциальные уравнения математической физики. М.: Физматгиз, 1962.
10. Петровский И. Г. Лекции об уравнениях с частными производны- ми. М.: Физматгиз, 1961.
11. Тихонов А. Н., Самарский А. А. Уравнения математической физии- ки. М.: Наука, 1966.
12. Будак Б. М., Самарский А. А., Тихонов А. Н. Сборник задач по математической физике. М.:Гостехиздат, 1956.
13. Смирнов М. М. Задачи по уравнениям математической физики. М.: Наука, 1968.
14. Сборник задач по уравнениям математической физике./ Под редакцией В.С.Владимирова. М.: Наука, 1974.
15. Бицадзе А. В., Колиниченко Д. Ф. Сборник задач по уравнениям математической физике. М.: Наука, 1977.
16. Русак В.Н. Математическая физика. Мн.: Дизайн ПРО, 1998.
Содержание
Предисловие..………………………………………………………………....3
§ 1.Ряды и преобразования Фурье…….……………………………………...4
§ 2.Операционное исчисление………………………………………………11
§ 3. Классификация и приведение к каноническому виду уравнений в
частных производных второго порядка……………………………….…..21
§ 4. Простейший вариант метода разделения переменных………………..27
§ 5. решение смешанной задачи с неоднородностями в уравнении или в граничных условиях……………………………………………………...…39
§ 6. Метод разделения переменных для параболических уравнений……49
§ 7. Цилиндрические функции и решение смешанных задач для уравнений
гиперболического и параболического типов………………………………60
§ 8. Метод разделения для уравнений эллиптического типа…………..…81
Литература………………………………………………………………….103
Учебное издание
Задачи по математической
и их решения
Авторы=составители:
Русак Валентин Николаевич,
Филиппова Нелли Константиновна.
В авторской редакции
Технический редактор Т. К. Раманович
Корректор О. Н. Кохно
Копьютерная верстка
Ответственный за выпуск Л. В. Рутковская
Подписано в печать 00.00.2006. Формат 
Бумага офсетная.
Гарнитура Таймс. Печать офсетная. Усл. печ. л. Уч. изд. Л. 4,0.
Тираж экз. Зак.
Белорусский государственный университет.
Лицензия на осуществление издательской деятельности
№02330/0056804 от 02.03.2004.
220050, Минск, проспект Независимости, 4.
Отпечатано с оригинала=макета заказчика.
Республиканское унитарное предприятие
«Издательский центр Белорусского государственного университета».
Лицензия на осуществление полиграфической деятельности
№02330/0056850 от 30.04.2004.
220050, Минск, ул. Красноармейская, 6.
