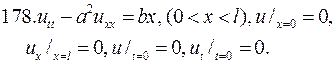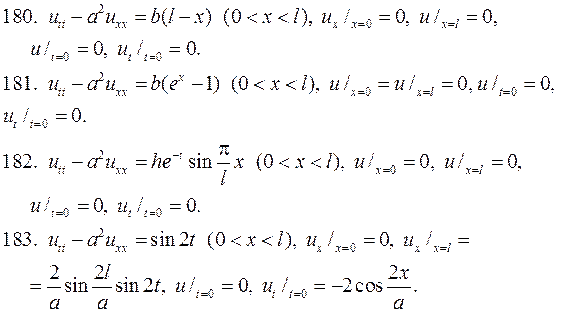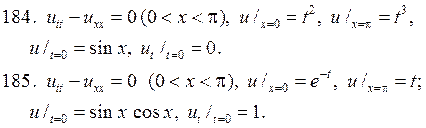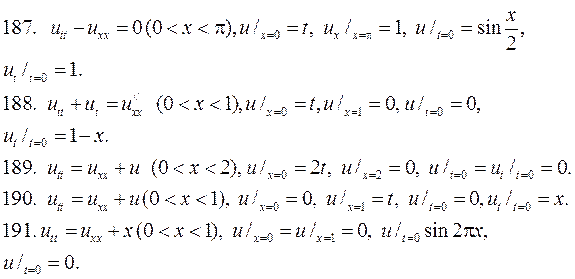ИЛИ В ГРАНИЧНЫХ УСЛОВИЯХ
Будем рассматривать смешанную задачу
и будем искать ее решение в виде суммы двух функций
u (x,t) =v (x,t) +w (x,t),
которые находятся из решения более простых задач. Функция v (x,t) у довлетворяет неоднородному уравнению с нулевыми граничными и начальными условиями
Соответственно функция w (x,t) есть решение смешанной задачи
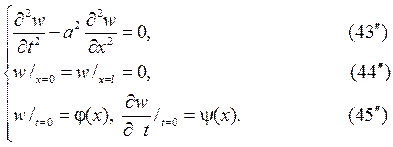
Нам нужно решать только штрихованную задачу (43¢) 
(45¢), посколь- ку задача (43¢¢) (45¢¢) совпадает с уже решенной в § 1 смешанной задачей (31)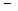 
(33), и следовательно (см.(40) 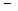(42))
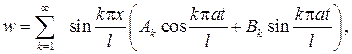
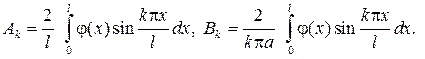(46)
Функцию v (x,t) следует разыскивать в виде ряда по собственным функ-
циям задачи (7-8) Штурма 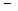Лиувилля:
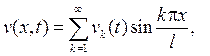(47)
где vk (t)нужно определить, используя соотношения(43¢) и (45¢). Гранич-ные условия (44¢) для функции v (x,t), очевидно, выполнены.
В свою очередь функцию f (x,t) разложим в ряд Фурье так, что
Подставляя (47) и (48) в (43¢) получаем тождество
и, стало быть, при всех t
(49)
После подстановки (17) в (14¢) найдем начальные условия для функций
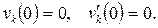(50)
Линейное дифференциальное уравнение (49) с присоединенными к нему начальными условиями (50) образуют стандартную задачу Коши, решение которой существует и единственно при данном k. Более того, нетрудно проверить, что решение задачи (49) (50) дается формулой
и подставляя ее в (48), получим решение штрихованной задачи
(51)
Складывая (46) и (51), найдем решение исходной задачи (43) (45).
Теперь займемся смешанной задачей для неоднородного уравнения с неоднородными граничными условиями
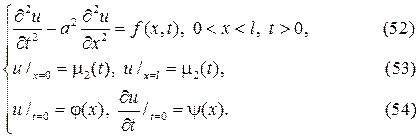
Простой прием позволяет свести данную задачу к уже исследованной задаче (43) (45). Действительно, и на этот раз полагая
u (x,t) = v (x,t) + w (x,t),
где v (x,t)новая неизвестная функция, перейдем к задаче
Мы не уточняем конкретные выражения функций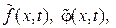 
, но ясно, что они находятся через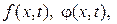 
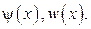Возьмем теперь функцию w (x,t)такой, чтобы выполнялись соотношения
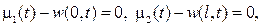(55)
нам подойдут в частности
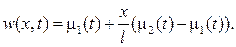
При выполнении условий (55) штрихованная задача (52¢) (54¢) переходит в уже решенную задачу (43) (45).
174. Жестко закрепленный в точке х =0 стержень l находится в состоянии покоя. В момент t =0 к его концу x=l приложена сила Q, действующая
вдоль стержня. Найти смещение точек стержня u (x,t) при t >0.
Р е ш е н и е. Текстовая задача равносильна смешанной задаче
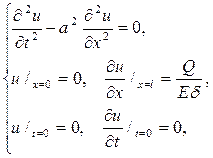
где Е – модуль упругости; и d - площадь поперечного сечения стержня.
Здесь нужно сделать замену
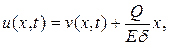
тогда неоднородность переместится в начальные условия и функция v (x,t)будет решением простейшей смешанной задачи
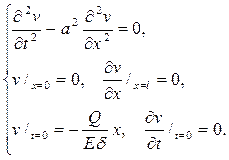
Как и при решении задачи 145, найдем, что
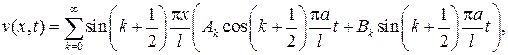
и подставляя ряд в первое начальное условие, будем иметь
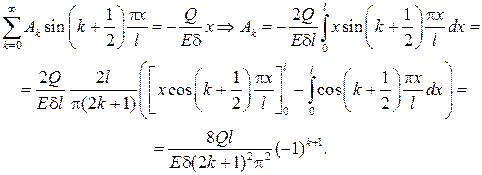
Из второго начального условия вытекает, что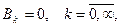 
поэтому окончательный ответ
175. Решите задачу о вынужденных продольных колебаниях стержня, закрепленного в конце х =0 и подверженного на другом конце x=l, дейст- вию возмущающей силы, которая вызывает смещение 
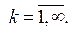В момент времени t =0 смещение и скорости отсутствуют.
Р е ш е н и е. Отклонение точек стержня u (x,t) от положения равнове -сия будет решением смешанной задачи
Решение этой задачи нужно искать в виде суммы
,
и относительно новой неизвестной функции v (x,t) будем иметь простей- шую смешанную задачу
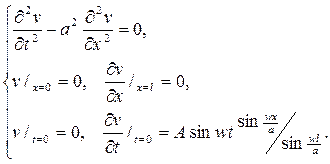
Ее решение будет представлено в виде ряда (см. решение задачи 144)
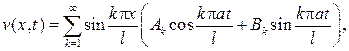
причем из первого начального условия вытекает, что Аk =0, а из второго начального условия следует
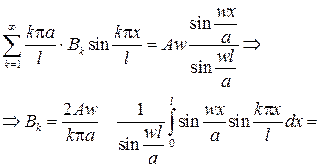
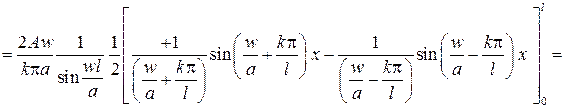
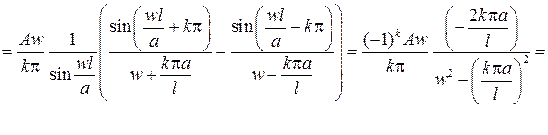
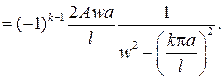
Все коэффициенты найдены, и тогда ответ будет иметь вид
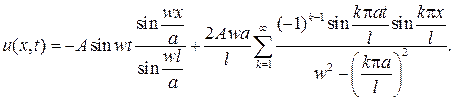
176. Решите уравнение вынужденных колебаний
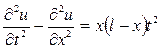
при нулевых начальных и граничных условиях 
Р е ш е н и е. Нужно решать смешанную задачу
Решение ищем в виде ряда, удовлетворяющего граничным условиям:
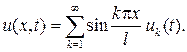
Правую часть уравнения также раскладываем в ряд Фурье 
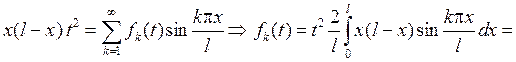
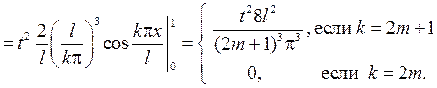
Подставляем эти ряды в исходное дифференциальное уравнение:
Из начальных условий для u (x,t) вытекает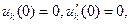 
т.е. нужно теперь решить задачи Коши
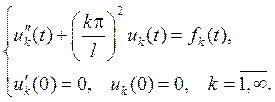
Если k= 2 m четное, то решением задачи Коши будет тривиальное решение uk º0. Если же k= 2 m+ 1 нечетное, то дифференциальное урав- нение
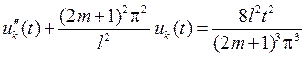
имеет частное решение в виде полинома
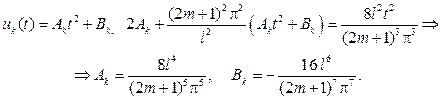
В таком случае общее решение будет иметь вид
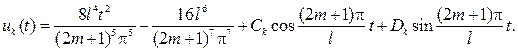
Из условия uk (0)=0 вытекает, что
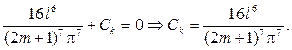
Из второго условия 
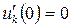получим, что Dk =0.
Итак, при нечетных k решением задачи Коши будет функция
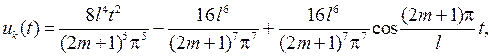
и соответственно решение рассматриваемой смешанной задачи примет вид
177. Решите задачу о продольных колебаниях u (x,t) стержня, подвешен -ного в концевой точке х= 0, совершаемых под влиянием силы тяжести, ес-ли
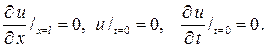
Р е ш е н и е: Здесь нужно рассматривать смешанную задачу
Вводим новую неизвестную функцию v (x,t), полагая
u (x,t) = v (x,t) + w (x)
и выбирая w (x) такой, чтобы для функции v (x,t) получить однородное уравнение и однородные граничные условия. Для этого нужно потре- бовать
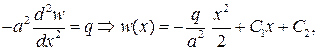
и далее выбрать константы из условий
В итоге получим, что
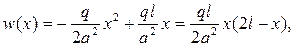
и для таким образом подобранной функции w (x) относительно v (x,t)
найдем простейшую смешанную задачу
Ее решение (как и в задаче 174) отыскивается в виде ряда с неопреде- ленными коэффициентами:
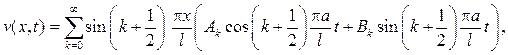
причем из условия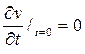 
следует 
а из первого начального условия имеем
С учетом найденных коэффициентов Bk, Ak, и w (x) ответ будет иметь вид
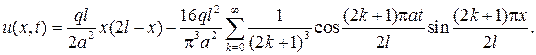
Решите следующие смешанные задачи.
