1. Общее уравнение плоскости
Ax + By + Cz + D = 0. (1)
Если в этом уравнении D = 0, то плоскость проходит через начало координат, и ее уравнение будет таким
Ax + By + Cz = 0. (2)
При C = 0 уравнение (1) примет вид
Ax + By + D = 0, (3)
и плоскость параллельна оси Oz.
При B = 0 уравнение (1) запишется в виде
Ax + Cz + D = 0. (4)
В этом случае плоскость параллельна оси Oy, а при A = 0 уравнение (1) приобретает вид
By + Cz + D = 0, (5)
и плоскость параллельна оси Ox.
Следует запомнить, что если плоскость параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью. Если в уравнениях (3), (4) и (5) окажется, что D = 0, то эти уравнения имеют вид
Ax + By = 0, (6)
Ax + Cz = 0, (7)
By + Cz = 0. (8)
Уравнение (6) - уравнение плоскости, проходящей через координатную ось Oz; (7) - уравнение плоскости, проходящей через ось Oy, а (8) - уравнение плоскости, проходящей через ось Ox. Если в уравнении (1) A = 0 и B = 0, то оно приобретет вид
Cz + D = 0, (9)
и плоскость параллельна координатной плоскости xOy. При B = 0 и C = 0 уравнение (1) запишется в виде
Ax + D = 0, (10)
а определяемая им плоскость параллельна координатной плоскости yOz. При A = 0 и C = 0 получаем из (1)
By + D = 0, (11)
и плоскость (11) параллельна координатной плоскости xOz.
Если окажется, что в уравнениях (9), (10) и (11) D = 0, то эти уравнения примут вид
z = 0, (12)
x = 0, (13)
y = 0 (14)
и будут уравнениями самих координатных плоскостей, соответственно xOy, yOz и xOz.
2. Уравнение плоскости в нормальном виде
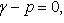(15)
где 
, 
и 
- углы между координатными осями Ox, Oy и Oz и перпендикуляром, опущенным из начала координат на плоскость, а p - длина этого перпендикуляра.
3. Для приведения общего уравнения плоскости (1) к нормальному виду (15) обе его части следует умножить на нормирующий множитель
(16)
выбрав перед корнем знак, противоположный знаку свободного члена в уравнении (1).
4. Уравнение плоскости в отрезках на осях
(17)
где a, b и c - величины отрезков, отсекаемых плоскостью на координатных осях.
5. Уравнение связки плоскостей, проходящей через точку M (x 1, y 1, z 1), имеет вид
A (x - x 1) + B (y - y 1) + C (z - z 1) = 0. (18)
Давая коэффициентам A, B и C в уравнении (18) различные значения, мы получим различные плоскости, проходящие через тчоку M (x 1, y 1, z 1).
6. Угол между двумя плоскостями
A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 (19)
определяется по формуле
(20)
7. Условие перпендикулярности двух плоскостей (19) имеет вид
A 1 A 2 + B 1 B 2 + C 1 C 2 = 0. (21)
8. Условие параллельности двух плоскостей (19) имеет вид
(22)
9. Расстояние от точки N (x 1, y 1, z 1) до плоскости Ax + By + Cz + D = 0 определяется по формуле
(23)
10. Система двух линейных однородных уравнений с тремя неизвестными:
(24)
Приведем относящиеся сюда формулы:
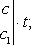
(25)
где t - произвольное число, а, по крайней мере, один из определителей, входящих в (25), не равен нулю.
11. Уравнение плоскости, проходящей через три данные точки A (x 1, y 1, z 1), B (x 2, y 2, z 2), C (x 3, y 3, z 3) имеет вид
(26)
